本格数学クイズ (解析幾何学)
座標幾何学
クイズ《光の照射範囲》
床の上の光源 $\mathrm O$ から, 天井から垂らされたスクリーン上の点 $\mathrm C$ に向かって光を照射したところ, 真横から見て, 光はスクリーンの下端 $\mathrm A$ から上端 $\mathrm B$ にまで達し, スクリーンの真下にある床の上の点を $\mathrm H$ として $\mathrm{OH} = \mathrm{HA} = \mathrm{AC}$ となった.
このとき, 点 $\mathrm B$ の床からの距離は点 $\mathrm A$ の床からの距離の何倍になるか.
(オリジナル)
答え
$7$ 倍.
解説
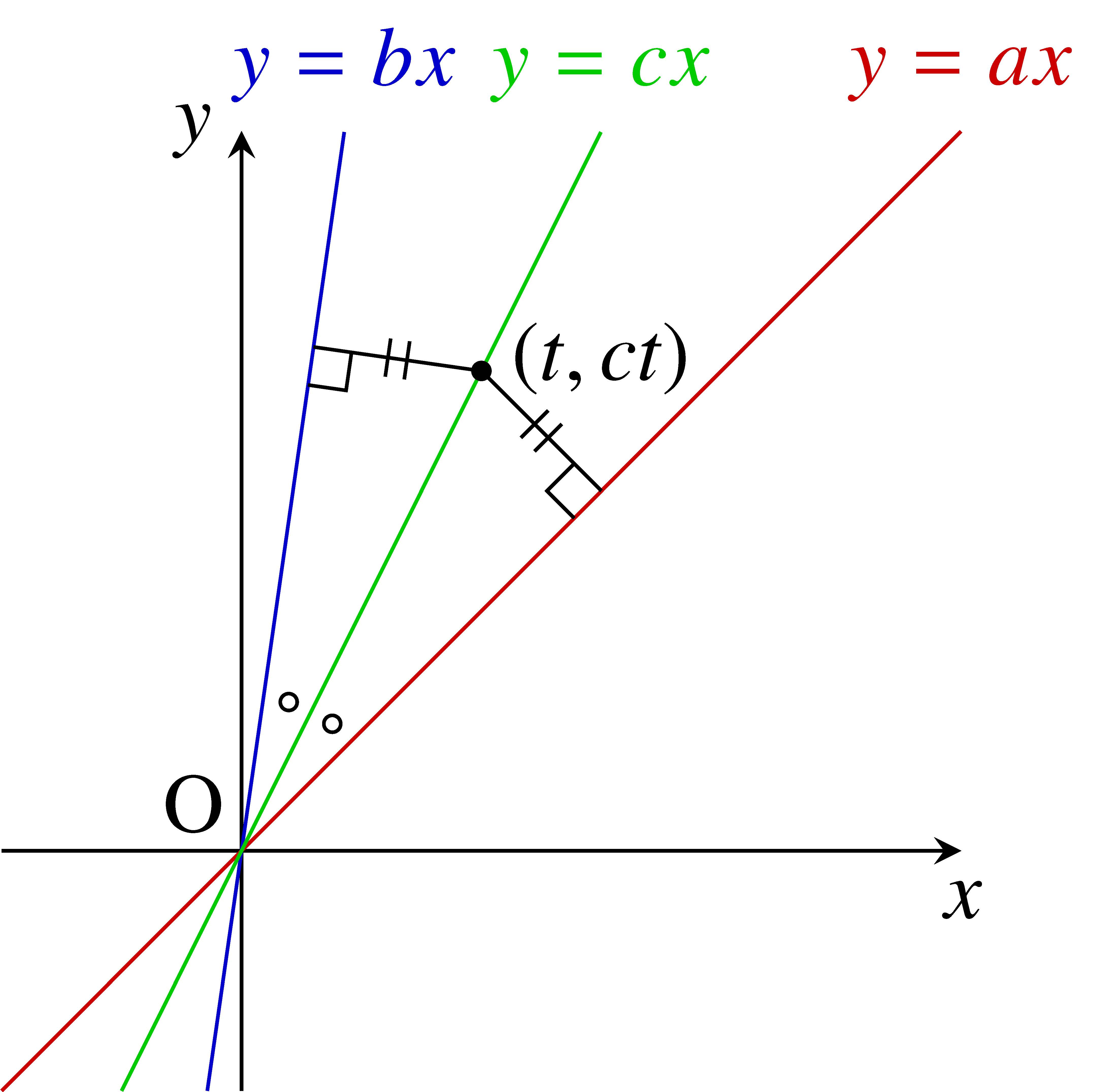
光源 $\mathrm O$ を原点, 床面を $x$ 軸とする $xy$ 平面を考え, 直線 $\mathrm{OA},$ $\mathrm{OB},$ $\mathrm{OC}$ の傾きをそれぞれ $a,$ $b,$ $c$ (いずれも正の数) とする.
光に性質により, 直線 $\mathrm{OC}:y = cx$ は $2$ 直線 $\mathrm{OA}:y = ax,$ $\mathrm{OB}:y = bx$ のなす角の二等分線である.
角の二等分線 $y = cx$ 上の点 $(t,ct)$ $(t \neq 0)$ と $2$ 直線 $ax-y = 0,$ $bx-y = 0$ の距離は等しいから,
\[\begin{aligned}
\frac{|at-ct|}{\sqrt{a^2+(-1)^2}} &= \frac{|bt-ct|}{\sqrt{b^2+(-1)^2}} \\
|a-c|\sqrt{b^2+1} &= |b-c|\sqrt{a^2+1}
\end{aligned}\]
が成り立つ.
 両辺を $2$ 乗すると
\[ (a-c)^2(b^2+1) = (b-c)^2(a^2+1) \quad \cdots [\ast ]\]
が得られる.
条件により
\[ a = \frac{\mathrm{HA}}{\mathrm{OH}} = 1, \quad c = \frac{\mathrm{HC}}{\mathrm{OH}} = \frac{\mathrm{HA}+\mathrm{AC}}{\mathrm{OH}} = 2\]
であるから, これを $[\ast ]$ に代入して $b$ について解くと
\[ b = 7\]
となる.
ゆえに, 点 $\mathrm B$ の床からの距離は点 $\mathrm A$ の床からの距離の
両辺を $2$ 乗すると
\[ (a-c)^2(b^2+1) = (b-c)^2(a^2+1) \quad \cdots [\ast ]\]
が得られる.
条件により
\[ a = \frac{\mathrm{HA}}{\mathrm{OH}} = 1, \quad c = \frac{\mathrm{HC}}{\mathrm{OH}} = \frac{\mathrm{HA}+\mathrm{AC}}{\mathrm{OH}} = 2\]
であるから, これを $[\ast ]$ に代入して $b$ について解くと
\[ b = 7\]
となる.
ゆえに, 点 $\mathrm B$ の床からの距離は点 $\mathrm A$ の床からの距離の
である.

| $\mathrm{HB}\div\mathrm{HA} = \dfrac{\mathrm{HB}}{\mathrm{OH}}\div\dfrac{\mathrm{HA}}{\mathrm{OH}} = b\div a = 7$ (倍) |
クイズ《等面四面体の体積》
たかし君は, $3$ 辺の長さが $a,$ $b,$ $c$ である鋭角三角形の板 $4$ 枚を貼り合わせて正四面体のオブジェを作った.
このオブジェの体積はいくらか.
(有名問題, 参考: $2014$ 早稲田大)
答え
$\dfrac{\sqrt{2(b^2+c^2-a^2)(c^2+a^2-b^2)(a^2+b^2-c^2)}}{12}.$
解説
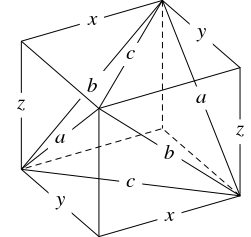
$3$ 辺の長さが $a,$ $b,$ $c$ である鋭角三角形 $4$ 枚を貼り合わせてできる正四面体は, 直方体から $4$ つの角 (互いに合同な三角錐) を取り除いて得られることに注意する.

- (1)
- まず, この直方体の横の長さ $x,$ 縦の長さ $y,$ 高さ $z$ を求める. $a,$ $b,$ $c$ はこの直方体において面の対角線の長さであるから, \[ y^2+z^2 = a^2, \quad z^2+x^2 = b^2, \quad x^2+y^2 = c^2\] が成り立つ. これら $3$ 式の辺々を加えて両辺を $2$ で割ると \[ x^2+y^2+z^2 = \frac{a^2+b^2+c^2}{2}\] となるから, \[\begin{aligned} x^2 &= \dfrac{b^2+c^2-a^2}{2}, \\ y^2 &= \dfrac{c^2+a^2-b^2}{2}, \\ z^2 &= \dfrac{a^2+b^2-c^2}{2} \end{aligned}\] つまり \[\begin{aligned} x &= \sqrt{\frac{b^2+c^2-a^2}{2}}, \\ y &= \sqrt{\frac{c^2+a^2-b^2}{2}}, \\ z &= \sqrt{\frac{a^2+b^2-c^2}{2}} \end{aligned}\] である.
- (2)
- (1) から, 求める正四面体の体積 $V$ は \[\begin{aligned} V &= xyz-4\cdot\frac{1}{3}\cdot\frac{1}{2}xy\cdot z = \frac{1}{3}xyz \\ &= \frac{\sqrt{2(b^2+c^2-a^2)(c^2+a^2-b^2)(a^2+b^2-c^2)}}{12} \end{aligned}\] である.
三角法
クイズ《オイラーの不等式》
円柱に $3$ 枚の薄い長方形の板を貼り付けて三角柱を作り, これを回転させることで新しい円柱を作る.
新しい円柱の半径が最小になるようにするとき, その半径はもとの円柱の半径の何倍になるか.
(オリジナル)
答え
$2$ 倍.
解説
求める値は, 単位円を外接円にもつ $\triangle\mathrm{ABC}$ の内接円の半径 $r$ の最大値の逆数に等しい.
この三角形において, 外心を $\mathrm O$ とおき, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB}$ とおく.
- (i)
- $\triangle\mathrm{ABC}$ が鋭角三角形の場合. $\mathrm O$ は $\triangle\mathrm{ABC}$ の内部にある. $\triangle\mathrm{OCA},$ $\triangle\mathrm{OAB}$ において底辺を $\mathrm{OA}$ としたときの高さの和は $a$ 以下であるから, \[\triangle\mathrm{OCA}+\triangle\mathrm{OAB} \leqq \frac{a}{2}\] が成り立つ. 同様に \[\begin{aligned} \triangle\mathrm{OAB}+\triangle\mathrm{OBC} &\leqq \frac{b}{2}, \\ \triangle\mathrm{OBC}+\triangle\mathrm{OCA} &\leqq \frac{c}{2} \\ \end{aligned}\] が成り立つから, 辺々を加えると \[\begin{aligned} r(a+b+c) = 2\triangle\mathrm{ABC} &\leqq \frac{a+b+c}{2} \\ r &\leqq \frac{1}{2} \end{aligned}\] が得られる.
- (ii)
- $\triangle\mathrm{ABC}$ が直角三角形, 鈍角三角形の場合.
$\mathrm O$ は $\triangle\mathrm{ABC}$ の辺上または外部にあり, $\triangle\mathrm{ABC}$ の内接円は半径 $1$ の半円の内部に収まるから,
が成り立つ.$2r < 1$ つまり $r < \dfrac{1}{2}$
参考
三角形の外接円の半径 $R,$ 内接円の半径 $r$ に対して, $R \geqq 2r$ が成り立つ.
この不等式は「オイラーの不等式」として知られている.
クイズ《三角形の外接円と内接円の半径の比》
$3$ 辺の長さと面積が整数である三角形は「ヘロンの三角形」と呼ばれ, その外接円, 内接円の半径が有理数であることはよく知られている.
それでは, $3$ 辺の長さが整数である三角形において外接円の半径に対する内接円の半径の比は有理数であるという主張は正しいか.
正しければ証明を与え, 誤りであれば反例を挙げよ.
(オリジナル, 参考: $2016$ 山口大)
答え
正しい (証明は解説を参照).
解説
$\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $s = \dfrac{a+b+c}{2}$ とおき, 面積, 外接円の半径, 内接円の半径をそれぞれ $S,$ $R,$ $r$ とおく.
- (1)
- 正弦定理により $\dfrac{a}{\sin\angle\mathrm A} = 2R$ であるから, \[ S = \frac{1}{2}bc\sin\angle\mathrm A = \frac{1}{2}bc\cdot\frac{a}{2R} = \frac{abc}{4R} \quad \cdots [1]\] が成り立つ.
- (2)
- $\triangle\mathrm{ABC}$ の内心を $\mathrm I$ とおくと, \[\begin{aligned} S &= \triangle\mathrm{IBC}+\triangle\mathrm{ICA}+\triangle\mathrm{IAB} \\ &= \frac{1}{2}ra+\frac{1}{2}rb+\frac{1}{2}rc = \frac{1}{2}r(a+b+c) \\ &= rs \quad \cdots [2] \end{aligned}\] となる.
- (3)
- $[1],$ $[2]$ と「ヘロンの公式」$S = \sqrt{s(s-a)(s-b)(s-c)}$ により, \[\begin{aligned} \frac{r}{R} &= \frac{S}{s}\div\frac{abc}{4S} = \frac{4S^2}{abcs} \\ &= \frac{4s(s-a)(s-b)(s-c)}{abcs} = \frac{4(s-a)(s-b)(s-c)}{abc} \\ &= \frac{(b+c-a)(c+a-b)(a+b-c)}{2abc} \end{aligned}\] が成り立つ. よって, $a,$ $b,$ $c$ が整数であれば, $\dfrac{r}{R}$ の値は有理数になる.
クイズ《球に入る最大の正多面体》
球状のカプセルにできるだけ体積の大きい正多面体の模型を入れたい.
どの正多面体の模型を入れればよいか.
(有名問題)
答え
正十二面体.
解説
$1$ 辺の長さが $1$ の正十二面体 $P_{12},$ 正二十面体 $P_{20}$ の外接球に占める体積の割合を比較する (正四面体, 正六面体, 正八面体の外接球に占める体積の割合がこれらより小さいことは以下と同様の計算からわかるが, 長くなるため証明は割愛する).
$\varphi = \dfrac{1+\sqrt 5}{2}$ とおく.
- (1)
- $P_i$ の外接球の半径 $R_i$ を求める.
- $P_{12}$ には $1$ 辺の長さが $\varphi$ の立方体 (頂点を $1$ つ飛ばしに結んで得られる) が内接するから, 最長対角線の長さ $d_{12}$ は \[ d_{12} = \sqrt{\varphi ^2+\varphi ^2+\varphi ^2} = \varphi\sqrt 3\] である. よって, 外接球の半径 $R_{12}$ は \[ R_{12} = \frac{d_{12}}{2} = \frac{\varphi\sqrt 3}{2} = \frac{\sqrt 3+\sqrt{15}}{4}\] である.
- $P_{20}$ の最長対角線は隣り合う $2$ 辺の長さが $1,$ $\varphi$ の長方形の対角線と一致するから, 最長対角線の長さ $d_{20}$ は \[ d_{20} = \sqrt{1^2+\varphi ^2} = \sqrt{1+\frac{3+\sqrt 5}{2}} = \sqrt{\frac{5+\sqrt 5}{2}} = \sqrt{\varphi\sqrt 5}\] である. よって, 外接球の半径 $R_{20}$ は \[ R_{20} = \frac{d}{2} = \frac{\sqrt{\varphi\sqrt 5}}{2} = \frac{\sqrt{10+2\sqrt 5}}{4}\] である.
- (2)
- $P_i$ の内接球の半径 $r_i$ を求める.
- $P_{12}$ の頂点と面の中心の距離 $l_{12}$ は面の外接球の半径に等しく \[ l_{12} = \frac{1}{2\sin 36^\circ} = \frac{2}{\sqrt{10-2\sqrt 5}}\] であるから, 内接球の半径 $r_{12}$ は三平方の定理により \[\begin{aligned} r_{12} &= \sqrt{R_{12}{}^2-l_{12}{}^2} = \sqrt{\frac{9+3\sqrt 5}{8}-\frac{5+\sqrt 5}{10}} \\ &= \sqrt{\frac{25+11\sqrt 5}{40}} = \frac{1}{2}\sqrt{\frac{25+11\sqrt 5}{10}} \end{aligned}\] である.
- $P_{20}$ の頂点と面の中心の距離 $l_{20}$ は面の外接球の半径に等しく \[ l_{20} = \frac{1}{2\sin 60^\circ} = \frac{1}{\sqrt 3}\] であるから, 内接球の半径 $r_{20}$ は三平方の定理により \[\begin{aligned} r_{20} &= \sqrt{R_{20}{}^2-l_{20}{}^2} = \sqrt{\frac{10+2\sqrt 5}{16}-\frac{1}{3}} \\ &= \sqrt{\frac{14+6\sqrt 5}{48}} = \sqrt{\frac{(3+\sqrt 5)^2}{48}} \\ &= \frac{3+\sqrt 5}{4\sqrt 3} = \frac{3\sqrt 3+\sqrt{15}}{12} \end{aligned}\] である.
- (3)
- $P_i$ の体積 $V_i$ を求める.
- $P_{12}$ は底面積が $\dfrac{\sqrt{25+10\sqrt 5}}{4},$ 高さが $r_{12}$ の正五角錐 $12$ 個に分けられるから, その体積 $V_{12}$ は \[\begin{aligned} V_{12} &= 12\cdot\left(\frac{1}{3}\cdot\frac{\sqrt{25+10\sqrt 5}}{4}\cdot\frac{1}{2}\sqrt{\frac{25+11\sqrt 5}{10}}\right) \\ &= \frac{1}{2}\sqrt{\frac{(25+10\sqrt 5)(25+11\sqrt 5)}{10}} = \frac{1}{2}\sqrt{\frac{1175+525\sqrt 5}{10}} \\ &= \frac{1}{2}\sqrt{\frac{470+210\sqrt 5}{4}} = \frac{\sqrt{(15+7\sqrt 5)^2}}{4} = \frac{15+7\sqrt 5}{4} \\ &= \frac{\varphi ^4\sqrt 5}{2} \end{aligned}\] である.
- $P_{20}$ は底面積が $\dfrac{\sqrt 3}{4},$ 高さが $r_{20}$ の正三角錐 $20$ 個に分けられるから, その体積 $V_{20}$ は \[\begin{aligned} V_{20} &= 20\cdot\left(\frac{1}{3}\cdot\frac{\sqrt 3}{4}\cdot\frac{3\sqrt 3+\sqrt{15}}{12}\right) = \frac{15+5\sqrt 5}{12} \\ &= \frac{5\varphi ^2}{6} \end{aligned}\] である.
- (4)
- 以上から, 正十二面体, 正二十面体の外接球に占める体積の割合はそれぞれ \[\begin{aligned} V_{12}\div\frac{4}{3}\pi R_{12}{}^3 &= \frac{\varphi\sqrt 5}{\pi\sqrt 3} \quad \cdots [1], \\ V_{20}\div\frac{4}{3}\pi R_{20}{}^3 &= \frac{\sqrt{\varphi\sqrt 5}}{\pi} \quad \cdots [2] \end{aligned}\] であることがわかり, \[ [1]\div [2] = \sqrt{\frac{\varphi\sqrt 5}{3}} = \sqrt{\frac{5+\sqrt 5}{6}} > 1\] により前者の方が大きいので, 正十二面体の模型を入れればよい.
参考
正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体の外接球に占める体積の割合はそれぞれ
\[\begin{aligned}
\frac{2\sqrt 3}{9\pi} &= 0.12251\cdots, \\
\frac{2\sqrt 3}{3\pi} &= 0.36755\cdots, \\
\frac{1}{\pi} &= 0.31830\cdots, \\
\frac{\varphi\sqrt{15}}{3\pi} &= 0.66490\cdots, \\
\frac{\sqrt{\varphi\sqrt 5}}{\pi} &= 0.60546\cdots
\end{aligned}\]
である.
クイズ《三角柱の側面の勾配》
三角柱のブロックを横にして平らな床で転がすと, 側面が床につく度に斜面の勾配が整数になった.
このとき, 各勾配の値はいくらか.
(オリジナル)
答え
$1,$ $2,$ $3.$
解説
内角の大きさが $\alpha,$ $\beta,$ $\gamma$ $(\alpha \leqq \beta \leqq \gamma )$ である直角三角形でない三角形において $\tan\alpha,$ $\tan\beta,$ $\tan\gamma$ が整数であるとして, それらの値を求めればよい.
- (1)
- まず, $\tan\alpha,$ $\tan\beta,$ $\tan\gamma$ が満たす関係式を求める. $\alpha +\beta +\gamma = \pi$ であるから, 加法定理により \[\begin{aligned} \tan\gamma &= \tan (\pi -\alpha -\beta ) = -\tan (\alpha +\beta ) \\ &= -\frac{\tan\alpha +\tan\beta}{1-\tan\alpha\tan\beta} \end{aligned}\] が成り立つ. 分母を払って整理すると, \[\begin{aligned} (\tan\alpha\tan\beta -1)\tan\gamma &= \tan\alpha +\tan\beta \\ \tan\alpha\tan\beta\tan\gamma &= \tan\alpha +\tan\beta +\tan\gamma \quad \cdots [1] \end{aligned}\] が得られる.
- (2)
- 次に, $\tan\alpha,$ $\tan\beta,$ $\tan\gamma$ の値を求める. 仮定 $\alpha \leqq \beta \leqq \gamma$ により \[ 3\alpha \leqq \alpha +\beta +\gamma = \pi\] であるから, $0 < \alpha \leqq \dfrac{\pi}{3}$ である. よって, \[ 0 < \tan\alpha \leqq \sqrt 3\] であり, $\tan\alpha$ は整数であるから, \[\tan\alpha = 1\] である. この値を $[1]$ に代入して整理すると, \[\begin{aligned} &\tan\beta\tan\gamma = \tan\beta +\tan\gamma +1 \\ &\tan\beta\tan\gamma -\tan\beta -\tan\gamma +1 = 2 \\ &(\tan\beta -1)(\tan\gamma -1) = 2 \end{aligned}\] が得られる. $\tan\beta,$ $\tan\gamma$ が整数であること, $\dfrac{\pi}{4} \leqq \beta \leqq \gamma,$ $\beta +\gamma = \dfrac{3}{4}\pi$ から $\beta,$ $\gamma$ は鋭角であって $1 \leqq \tan\beta \leqq \tan\gamma$ であることに注意すると, \[ (\tan\beta -1,\tan\gamma -1) = (1,2)\] つまり \[ (\tan\beta,\tan\gamma ) = (2,3)\] がわかる. ゆえに, 求める値は $1,$ $2,$ $3$ である.
クイズ《傾きの関係式》
ある街に $3$ つの坂があり, 最も緩い坂の斜度は他の $2$ つの坂の斜度の差に等しいという.
鉛直方向に $1$ m 上るために水平方向に進まなければならない距離が最もきつい坂で $x$ m, $2$ 番目にきつい坂で $(x+1)$ m であるとき, この距離は最も緩い坂で何 m になるか.
(オリジナル)
答え
$(x^2+x+1)$ m.
解説
最もきつい坂の斜度を $\alpha,$ $2$ 番目にきつい坂の斜度を $\beta$ とおく.
このとき,
\[\tan\alpha = \frac{1}{x}, \quad \tan\beta = \frac{1}{x+1}\]
が成り立つ.
条件から最も緩い坂の斜度は $\alpha -\beta$ であり, その傾きは
\[\begin{aligned}
\tan (\alpha -\beta ) &= \frac{\tan\alpha -\tan\beta}{1+\tan\alpha\tan\beta} = \frac{\dfrac{1}{x}-\dfrac{1}{x+1}}{1+\dfrac{1}{x}\cdot\dfrac{1}{x+1}} \\
&= \frac{(x+1)-x}{x(x+1)+1} = \frac{1}{x^2+x+1}
\end{aligned}\]
である.
ゆえに, 鉛直方向に $1$ m 上るために水平方向に進まなければならない距離は最も緩い坂で $(x^2+x+1)$ m である.
参考
$\tan x$ $\left( -\dfrac{\pi}{2} < x < \dfrac{\pi}{2}\right)$ の逆関数を $\arctan x$ で表すとき,
\[\arctan\frac{1}{x} = \arctan\frac{1}{x+1}+\arctan\frac{1}{x^2+x+1}\]
が成り立つ.
この公式はオイラーによって発見された.
クイズ《正接の和の最小値》
大きな鋭角三角形のオブジェを作る.
三角形の各頂点から反時計周りに辺に沿って $1$ だけ進んだ点から進行方向に対して垂直な方向に辺にぶつかるまで支柱を伸ばす.
$3$ 本の支柱の長さの和を最小にするには, オブジェをどうような形にすればよいか.
(オリジナル)
答え
正三角形.
解説
鋭角三角形の $3$ つの角の大きさを $A,$ $B,$ $C$ とおく.
このとき, $3$ 本の支柱の長さは $\tan A,$ $\tan B,$ $\tan C$ と表されるから,
\[ L = \tan A+\tan B+\tan C\]
の最小値を求める.
仮定によりこれらの値は正であるから, 相加・相乗平均の不等式により,
\[\frac{L}{3} \geqq \sqrt[3]{\tan A\tan B\tan C}\]
よって
\[ L^3 \geqq 27\tan A\tan B\tan C\]
が成り立つ.
前問で示した通り
\[\tan A\tan B\tan C = \tan A+\tan B+\tan C\]
であるから,
が成り立つ.
等号成立は, $\tan A = \tan B = \tan C,$ つまり $A = B = C$ のときに限る.
よって, 支柱の長さを最小にするには, 正三角形にすればよい.
| $L^3 \geqq 27L,$ $L^2 \geqq 27,$ つまり $L \geqq 3\sqrt 3$ |
よって, 支柱の長さを最小にするには, 正三角形にすればよい.
クイズ《楕円に内接する三角形》
楕円に内接する三角形について, 楕円に占める三角形の面積の割合は最大でいくらになるか.
(オリジナル)
答え
$\dfrac{3\sqrt 3}{4\pi} = 0.41349\cdots.$
解説
平行移動, 回転移動により, 楕円 $C:\dfrac{x^2}{p^2}+\dfrac{y^2}{q^2} \leqq 1$ $(p,\ q > 0)$ について考えれば十分である.
$C$ は単位円 $C_0:x^2+y^2 \leqq 1$ を $x$ 軸方向に $p$ 倍, $y$ 軸方向に $q$ 倍に拡大した図形である.
よって, $C$ に内接する三角形 $T$ を $x$ 軸方向に $p^{-1}$ 倍, $y$ 軸方向に $q^{-1}$ 倍に拡大した三角形が $T_0$ で, $T$ の面積が $S,$ $T_0$ の面積が $S_0$ であるとき, $T$ が $C$ に占める面積の割合は
\[\frac{S}{\pi pq} = \frac{pqS_0}{\pi pq} = \frac{S_0}{\pi}\]
で, $T_0$ が $C_0$ に占める面積の割合に等しい.
そこで, $C_0$ に内接する三角形 $\mathrm{ABC}$ の面積 $S_0$ の最大値を求める.
$a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB}$ とおく.
正弦定理により
\[\sin A = \frac{a}{2} \quad \cdots [1]\]
であるから,
\[ S = \frac{1}{2}bc\sin A = \frac{abc}{4}\]
が成り立つ.
相加・相乗平均の関係
\[\sqrt[3]{xyz} \leqq \frac{x+y+z}{3} \quad \cdots [2]\]
を $x = a^3,$ $y = b^3,$ $z = c^3$ (いずれも正の数) に適用すると,
\[ abc = \sqrt[3]{a^3b^3c^3} \leqq \frac{a^3+b^3+c^3}{3} \quad \cdots [3] \]
が得られる.
$[2]$ の等号成立条件は $x = y = z$ であるから, $[3]$ で等号が成立するのは $a = b = c$ の場合に限る.
$a = b = c$ のとき, $3$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ は正三角形をなし, $[1]$ から $a = 2\sin 60^\circ = \sqrt 3$ であるので,
\[ abc = \dfrac{3a^3}{3} = a^3 = 3\sqrt 3\]
が成り立つ.
したがって, これが $abc$ の最大値で, $S$ の最大値は
\[\frac{3\sqrt 3}{4}\]
である.
ゆえに, 求める最大値は
\[\frac{3\sqrt 3}{4}\div\pi = \frac{3\sqrt 3}{4\pi}\]
である.
参考
楕円に内接する $n$ 角形について, 楕円に占める $n$ 角形の面積の割合は, $n$ 角形が正 $n$ 角形を対称軸を基準に拡大・縮小したものであるとき, 最大で $\dfrac{n}{2\pi}\sin\dfrac{2\pi}{n}$ になる.
クイズ《ヘロンの公式》
$3$ 辺の長さが $a,$ $b,$ $c$ である三角形の面積 $S$ はどのように表されるか.
(有名問題, 参考: $2019$ 京都府立大, $2010$ 大阪教育大ほか)
答え
$S = \sqrt{s(s-a)(s-b)(s-c)}$ $\left( s = \dfrac{a+b+c}{2}\right).$
解説
$\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $s = \dfrac{a+b+c}{2}$ とおく.
このとき, 三角比の相互関係, 余弦定理により,
\[\begin{aligned}
&(\triangle\mathrm{ABC})^2 = \frac{1}{4}b^2c^2\sin ^2\angle\mathrm A \\
&= \frac{1}{4}b^2c^2(1-\cos ^2\angle\mathrm A) \\
&= \frac{1}{4}b^2c^2-\frac{1}{4}b^2c^2\cdot\frac{(b^2+c^2-a^2)^2}{4b^2c^2} \\
&= \frac{1}{16}\{ (2bc)^2-(b^2+c^2-a^2)^2\} \\
&= \frac{1}{16}(2bc+b^2+c^2-a^2)(2bc-b^2-c^2+a^2) \\
&= \frac{1}{16}\{ (b+c)^2-a^2\}\{ a^2-(b-c)^2\} \\
&= \frac{a+b+c}{2}\cdot\frac{b+c-a}{2}\cdot\frac{c+a-b}{2}\cdot\frac{a+b-c}{2} \\
&= s(s-a)(s-b)(s-c)
\end{aligned}\]
が成り立つ.
よって, 両辺の正の平方根をとると,
\[\triangle\mathrm{ABC} = \sqrt{s(s-a)(s-b)(s-c)}\]
が得られる.
参考
本問の公式は「ヘロンの公式」(Heron's formula) として知られている (別証明はこちらを参照).
クイズ《ブラーマグプタの公式とパラメシュヴァーラの公式》
- (1)
- 円に内接し, $4$ 辺の長さが $a,$ $b,$ $c,$ $d$ である四角形の $S$ は $a,$ $b,$ $c,$ $d$ を用いてどのように表されるか.
(有名問題, 参考: $2021$ 山口大,$2019$ 京都府立大ほか)
- (2)
- $4$ 辺の長さが $a,$ $b,$ $c,$ $d$ である四角形が円に内接するとき, その半径 $R$ は $a,$ $b,$ $c,$ $d$ を用いてどのように表されるか. (ヒント: 円に内接する四角形 $\mathrm{ABCD}$ において $\mathrm{AC}\cdot\mathrm{BD} = \mathrm{AB}\cdot\mathrm{CD}+\mathrm{BC}\cdot\mathrm{DA}$ が成り立つという「トレミーの定理」を用いる.)
答え
$s = \dfrac{a+b+c+d}{2}$ として,
- (1)
- $S = \sqrt{(s-a)(s-b)(s-c)(s-d)}.$
- (2)
- $\displaystyle R = \frac{1}{4}\sqrt{\frac{(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}}.$
解説
半径 $R$ の円に内接する四角形 $\mathrm{ABCD}$ において, $a = \mathrm{AB},$ $b = \mathrm{BC},$ $c = \mathrm{CD},$ $d = \mathrm{DA},$ $s = \dfrac{a+b+c+d}{2}$ とおき, 面積を $S$ とおく.
- (1)
- $\theta = \angle\mathrm{ABC}$ とおく. このとき, $\angle\mathrm{CDA} = 180^\circ -\theta$ であるから, \[\begin{aligned} S &= \triangle\mathrm{ABC}+\triangle\mathrm{CDA} \\ &= \frac{1}{2}ab\sin \theta +\frac{1}{2}cd\sin (180^\circ -\theta ) \\ &= \frac{1}{2}(ab+cd)\sin\theta \\ &= \frac{1}{2}(ab+cd)\sqrt{1-\cos ^2\theta} \end{aligned}\] が成り立つ. $\cos (180^\circ -\theta ) = -\cos\theta$ であるから, $\triangle\mathrm{ABC},$ $\triangle\mathrm{CDA}$ に余弦定理を適用すると \[\mathrm{AC}^2 = a^2+b^2-2ab\cos\theta = c^2+d^2+2cd\cos\theta \] となり, \[\cos\theta = \frac{a^2+b^2-c^2-d^2}{2(ab+cd)}\] となる. よって, \[\begin{aligned} S^2 &= \frac{1}{4}(ab+cd)^2(1-\cos ^2\theta ) \\ &= \frac{1}{4}(ab+cd)^2-\frac{1}{4}(ab+cd)^2\cdot\frac{(a^2+b^2-c^2-d^2)^2}{4(ab+cd)^2} \end{aligned}\] \[\begin{aligned} &= \frac{1}{16}\{ 4(ab+cd)^2-(a^2+b^2-c^2-d^2)^2\} \\ &= \frac{1}{16}\{ (2ab+2cd)^2-(a^2+b^2-c^2-d^2)^2\} \\ &= \frac{1}{16}(2ab+2cd-a^2-b^2+c^2+d^2) \\ &\qquad \cdot (2ab+2cd+a^2+b^2-c^2-d^2) \\ &= \frac{1}{16}\{ (c+d)^2-(a-b)^2\}\{ (a+b)^2-(c-d)^2\} \\ &= \frac{-a+b+c+d}{2}\cdot\frac{a-b+c+d}{2} \\ &\qquad \cdot\frac{a+b-c+d}{2}\cdot\frac{a+b+c-d}{2} \\ &= (s-a)(s-b)(s-c)(s-d) \end{aligned}\] が成り立つから, 両辺の正の平方根をとると \[ S = \sqrt{(s-a)(s-b)(s-c)(s-d)}\] が得られる.
- (2)
- $x = \mathrm{AC},$ $y = \mathrm{BD}$ とおく. $\triangle\mathrm{ABC},$ $\triangle\mathrm{ADC},$ $\triangle\mathrm{BAD},$ $\triangle\mathrm{BCD}$ も半径 $R$ の円に外接し, 一般に半径 $R$ に内接する $\triangle\mathrm{ABC}$ の面積は \[\frac{1}{2}\mathrm{AB}\cdot\mathrm{AC}\sin\angle\mathrm A = \frac{1}{2}\mathrm{AB}\cdot\mathrm{AC}\cdot\frac{\mathrm{BC}}{2R} = \frac{\mathrm{BC}\cdot\mathrm{CA}\cdot\mathrm{AB}}{4R}\] であるから, \[\begin{aligned} S &= \triangle\mathrm{ABC}+\triangle\mathrm{ADC} \\ &= \frac{abx}{4R}+\frac{cdx}{4R} \\ &= \frac{(ab+cd)x}{4R} \quad \cdots [1] \\ S &= \triangle\mathrm{BAD}+\triangle\mathrm{BCD} \\ &= \frac{ady}{4R}+\frac{bcy}{4R} \\ &= \frac{(ad+bc)y}{4R} \quad \cdots [2] \end{aligned}\] が成り立つ. $[1],$ $[2]$ の辺々を掛けると,「トレミーの定理」により \[\begin{aligned} S^2 &= \frac{(ab+cd)xy(ad+bc)}{16R^2} \\ &= \frac{(ab+cd)(ac+bd)(ad+bc)}{16R^2} \end{aligned}\] が得られる. これを $R$ について解き, (1) の公式を使うと \[\begin{aligned} R &= \frac{\sqrt{(ab+cd)(ac+bd)(ad+bc)}}{4S} \\ &= \frac{\sqrt{(ab+cd)(ac+bd)(ad+bc)}}{4\sqrt{(s-a)(s-b)(s-c)(s-d)}} \\ &= \frac{1}{4}\sqrt{\frac{(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}} \end{aligned}\] が得られる.
参考
- (1) の公式は「ブラーマグプタの公式」(Brahmagupta's formula) として知られている. 便宜的に $d = 0$ とすると, 上述の「ヘロンの公式」が得られる.
- $n \geqq 5$ のとき, 円に内接する $n$ 角形の面積を辺の長さをもとに加減乗除または累乗根をとる操作の繰り返しで表す公式は存在しないことが, 近年, ヴァルフォロメーエフ, および松本幸夫氏らにより,「ガロア理論」を用いて独立に証明された. 例えば, $5$ 辺の長さが $1,$ $1,$ $2,$ $3,$ $4$ である五角形は円に内接するが, その面積は有理数から加減乗除または累乗根をとる操作の繰り返しで表せないことが知られている (参考文献: Y. Matsumoto, Y. Matsutani, M. Oka, T. Sakai and T. Shibuya, On the area of a polygon inscribed in a circle, L'Enseignement Mathématique (2) 53 (2007), 127–153).
- 「ブラーマグプタの公式」は, 一般の四角形の面積に関する「ブレートシュナイダーの公式」(Bretschneider's formula) \[ S = \sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos ^2\frac{\theta}{2}}\] ($\theta$: $1$ 組の向かい合う角の和) に一般化される (こちらを参照).
- (2) の公式は「パラメシュヴァーラの公式」(Parameshvara's formula) として知られている.
クイズ《三角形の等周問題》
周の長さが一定の三角形のうち面積が最大のものはどのような形の三角形か.
(有名問題)
答え
正三角形.
解説
周の長さが $1$ の三角形について考えれば十分である.
この三角形において, $3$ 辺の長さを $a,$ $b,$ $c,$ 面積を $S$ とおく.
「ヘロンの公式」により,
\[ S = \sqrt{\frac{1}{2}\left(\frac{1}{2}-a\right)\left(\frac{1}{2}-b\right)\left(\frac{1}{2}-c\right)}\]
が成り立つ.
よって, 相加・相乗平均の不等式
\[\frac{x+y+z}{3} \geqq \sqrt[3]{xyz} \quad \cdots [\ast ]\]
と等号成立が $x = y = z$ の場合に限ることから,
\[\begin{aligned}
16S^2 &= (1-2a)(1-2b)(1-2c) \\
&\leqq \left\{\frac{(1-2a)+(1-2b)+(1-2c)}{3}\right\} ^3 \\
&= \left\{\frac{3-2(a+b+c)}{3}\right\} ^3 = \left(\frac{3-2\cdot 1}{3}\right) ^3 \\
&= \frac{1}{27}
\end{aligned}\]
であり, 等号成立は $1-2a = 1-2b = 1-2c$ つまり $a = b = c$ の場合に限る.
ゆえに, $S$ は $a = b = c$ の場合に限り最大になるから, 周の長さが一定の三角形のうち面積が最大のものは正三角形である.
なお, 不等式 $[\ast ]$ は, 次のように証明できる. $X = \sqrt[3]{x},$ $Y = \sqrt[3]{y},$ $Z = \sqrt[3]{z}$ とおくと \[\begin{aligned} &x+y+z-3\sqrt[3]{xyz} \\ &= X^3+Y^3+Z^3-3XYZ \\ &= (X+Y+Z)(X^2+Y^2+Z^2-XY-YZ-ZX) \\ &= (X+Y+Z)\cdot\frac{(X-Y)^2+(Y-Z)^2+(Z-X)^2}{2} \\ &\geqq 0 \end{aligned}\] となるから, 不等式 $[\ast ]$ が成り立ち, 等号成立は $X-Y = Y-Z = Z-X = 0,$ $X = Y = Z,$ つまり $x = y = z$ の場合に限る.
なお, 不等式 $[\ast ]$ は, 次のように証明できる. $X = \sqrt[3]{x},$ $Y = \sqrt[3]{y},$ $Z = \sqrt[3]{z}$ とおくと \[\begin{aligned} &x+y+z-3\sqrt[3]{xyz} \\ &= X^3+Y^3+Z^3-3XYZ \\ &= (X+Y+Z)(X^2+Y^2+Z^2-XY-YZ-ZX) \\ &= (X+Y+Z)\cdot\frac{(X-Y)^2+(Y-Z)^2+(Z-X)^2}{2} \\ &\geqq 0 \end{aligned}\] となるから, 不等式 $[\ast ]$ が成り立ち, 等号成立は $X-Y = Y-Z = Z-X = 0,$ $X = Y = Z,$ つまり $x = y = z$ の場合に限る.
別解
周の長さが $1$ の三角形について考えれば十分である.
周の長さが $1,$ 底辺の長さが $x$ $(0 < x < 1)$ の三角形のうち面積が最大になるのは, 高さが最大になる, 二等辺三角形である.
このような三角形について, 等辺の長さは $\dfrac{1-x}{2}$ であるから, 面積を $S(x)$ とおくと,
\[ S(x) = \frac{1}{2}x\sqrt{\left(\frac{1-x}{2}\right)^2-\left(\frac{x}{2}\right) ^2} = \frac{1}{4}x\sqrt{1-2x}\]
となり,
\[ 16S(x)^2 = x^2(1-2x)\]
となる.
右辺を $x$ の関数として, $f(x)$ とおく.
このとき, $f(x) = x^2-2x^3$ から
\[ f'(x) = 2x-6x^2 = 2x(1-3x),\]
であるので,
\[\begin{aligned}
f'(x) \geqq 0 &\iff 0 < x \leqq \frac{1}{3}, \\
f'(x) \leqq 0 &\iff \frac{1}{3} \leqq x < 1
\end{aligned}\]
が成り立つ.
よって, $f(x)$ は $x = \dfrac{1}{3}$ のとき極大かつ最大の値をとる.
したがって, $S(x)$ は $x = \dfrac{1}{3},$ つまり三角形が正三角形のとき最大値をとる.
ゆえに, 周の長さが一定の三角形のうち面積が最大のものは正三角形である.
クイズ《座標法》
頂点の座標が $(x_1,y_1),$ $\cdots,$ $(x_n,y_n)$ である $n$ 角形の面積 $S$ はどのように表されるか.
(有名問題)
答え
$S = \displaystyle\frac{1}{2}\left|\sum_{k = 1}^n(x_ky_{k+1}-y_kx_{k+1})\right|.$
解説
- (1)
- 複素数 $z$ の虚部を $\mathrm{Im}\,(z)$ で表す.
このとき, 複素数平面上の $n$ 角形 $z_1z_2\cdots z_n$ の面積 $S$ は
\[ S = \displaystyle\frac{1}{2}\left|\sum_{k = 1}^n\mathrm{Im}\,(\overline{z_k}z_{k+1})\right|\]
であり, 絶対値記号の中は頂点の並び方が反時計回りのとき正, 時計回りのとき負であることを示す.
ただし, $z_{n+1} = z_1$ とする.
- (I)
- $n = 3$ のとき.
- (i)
- $z_3 = 0$ のとき. $\theta = \mathrm{arg}\,\dfrac{z_2}{z_1}$ $(-\pi < \theta < \pi,$ $\theta \neq 0)$ とおく. $\cos\theta +i\sin\theta = \dfrac{|z_1|}{|z_2|}\cdot\dfrac{z_2}{z_1}$ であるから, $\mathrm{Im}\,(z) = \dfrac{z-\overline{z}}{2i}$ により \[\begin{aligned} \sin\theta &= \frac{|z_1|}{|z_2|}\mathrm{Im}\left(\frac{z_2}{z_1}\right) = \frac{|z_1|}{|z_2|}\cdot\frac{1}{2i}\left(\frac{z_2}{z_1}-\frac{\overline{z_2}}{\overline{z_1}}\right) \\ &= \frac{|z_1|}{|z_2|}\cdot\frac{1}{2i}\cdot\frac{\overline{z_1}z_2-z_1\overline{z_2}}{|z_1|^2} = \frac{1}{|z_1||z_2|}\mathrm{Im}\,(\overline{z_1}z_2) \end{aligned}\] が成り立つ. よって, \[ S = \frac{1}{2}|z_1||z_2|\left|\sin\theta\right| = \frac{1}{2}|\mathrm{Im}\,(\overline{z_1}z_2)|\] が成り立つ. $\mathrm{Im}\,(\overline{z_1}z_2)$ の符号は, $\sin\theta$ の符号, つまり $\theta = \mathrm{arg}\,\dfrac{z_2}{z_1}$ の符号と一致する.
- (ii)
- 一般の場合. 平行移動しても面積は変わらないから, (i) において $z_1,$ $z_2,$ $z_3$ を $w_1 = z_1-z_3,$ $w_2 = z_2-z_3,$ $0$ に置き換えると, $\mathrm{Im}\,(z+w) = \mathrm{Im}\,(z)+\mathrm{Im}\,(w),$ $\mathrm{Im}\,(\overline{z}) = -\mathrm{Im}\,(z)$ により \[\begin{aligned} S &= \frac{1}{2}|\mathrm{Im}\,(\overline{w_1}w_2)| = \frac{1}{2}\left|\mathrm{Im}\,((\overline{z_1}-\overline{z_3})(z_2-z_3))\right| \\ &= \frac{1}{2}\left|\mathrm{Im}\,(\overline{z_1}z_2-z_2\overline{z_3}-z_3\overline{z_1}+|z_3|^2)\right| \\ &= \frac{1}{2}\left|\mathrm{Im}\,(\overline{z_1}z_2)-\mathrm{Im}\,(z_2\overline{z_3})-\mathrm{Im}\,(z_3\overline{z_1})\right| \\ &= \frac{1}{2}\left|\mathrm{Im}\,(\overline{z_1}z_2)+\mathrm{Im}\,(\overline{z_2}z_3)+\mathrm{Im}\,(\overline{z_3}z_1)\right| \end{aligned}\] が得られる. 絶対値記号の中は, $\mathrm{arg}\,\dfrac{w_2}{w_1} = \mathrm{arg}\,\dfrac{z_2-z_3}{z_1-z_3}$ と符号が一致するから, 頂点の並び方が反時計回りのとき正, 時計回りのとき負である.
- (II)
- $n = m-1$ ($m$: $4$ 以上の整数) のとき公式が成り立つとし, $n = m$ の場合を考える.
$m-1$ 角形 $\mathrm P_1\cdots\mathrm P_{m-1}$ の面積を $S'$ とおく.
- 点 $\mathrm P_m$ が $m-1$ 角形 $\mathrm P_1\cdots\mathrm P_{m-1}$ の外部にあるとき. \[\begin{aligned} S &= S'+\triangle\mathrm P_1\mathrm P_{m-1}\mathrm P_m \\ &= \frac{1}{2}\left|\sum_{k = 1}^{m-2}\mathrm{Im}\,(\overline{z_k}z_{k+1})+\mathrm{Im}\,(\overline{z_{m-1}}z_1)\right| \\ &\qquad +\frac{1}{2}\left|\mathrm{Im}\,(\overline{z_1}z_{m-1})+\mathrm{Im}\,(\overline{z_{m-1}}z_m)+\mathrm{Im}\,(\overline{z_m}z_1)\right| \\ &= \frac{1}{2}\left|\sum_{k = 1}^{m-2}\mathrm{Im}\,(\overline{z_k}z_{k+1})+\mathrm{Im}\,(\overline{z_{m-1}}z_1)+\mathrm{Im}\,(\overline{z_1}z_{m-1})\right. \\ &\qquad \left.+\mathrm{Im}\,(\overline{z_{m-1}}z_m)+\mathrm{Im}\,(\overline{z_m}z_1)\right| \\ &= \frac{1}{2}\left|\sum_{k = 1}^m\mathrm{Im}\,(\overline{z_k}z_{k+1})\right| \end{aligned}\] が成り立つ.
- 点 $\mathrm P_m$ が $m-1$ 角形 $\mathrm P_1\cdots\mathrm P_{m-1}$ の内部にあるとき. この $m-1$ 角形と $\triangle\mathrm P_1\mathrm P_m\mathrm P_{m-1}$ の頂点の並び方は同じであるから, \[\begin{aligned} S &= S'-\triangle\mathrm P_1\mathrm P_m\mathrm P_{m-1} \\ &= \frac{1}{2}\left|\sum_{k = 1}^{m-2}\mathrm{Im}\,(\overline{z_k}z_{k+1})+\mathrm{Im}\,(\overline{z_{m-1}}z_1)\right| \\ &\qquad -\frac{1}{2}\left|\mathrm{Im}\,(\overline{z_1}z_m)+\mathrm{Im}\,(\overline{z_m}z_{m-1})+\mathrm{Im}\,(\overline{z_{m-1}}z_1)\right| \\ &= \frac{1}{2}\left|\sum_{k = 1}^{m-2}\mathrm{Im}\,(\overline{z_k}z_{k+1})+\mathrm{Im}\,(\overline{z_{m-1}}z_1)-\mathrm{Im}\,(\overline{z_1}z_m)\right. \\ &\qquad \left.-\mathrm{Im}\,(\overline{z_m}z_{m-1})-\mathrm{Im}\,(\overline{z_{m-1}}z_1)\right| \\ &= \frac{1}{2}\left|\sum_{k = 1}^m\mathrm{Im}\,(\overline{z_k}z_{k+1})\right| \end{aligned}\] が成り立つ.
- (2)
- (1) において, $z_1 = x_1+y_1i,$ $\cdots,$ $z_n = x_n+y_ni$ ($x_k,$ $y_k$: 実数) とすると, \[\begin{aligned} S &= \frac{1}{2}\left|\mathrm{Im}\left(\sum_{k = 1}^n\overline{z_k}z_{k+1}\right)\right| = \frac{1}{2}\left|\sum_{k = 1}^n\mathrm{Im}(\overline{z_k}z_{k+1})\right| \\ &= \frac{1}{2}\left|\sum_{k = 1}^n\mathrm{Im}(x_k-y_ki)(x_{k+1}+y_{k+1}i)\right| \\ &= \frac{1}{2}\left|\sum_{k = 1}^n(x_ky_{k+1}-y_kx_{k+1})\right| \end{aligned}\] が得られる.
参考
上記の公式は「座標法」と呼ばれ, 測量でよく利用されている.
式と曲線
クイズ《棒の継ぎ目の軌跡》
長さが $a,$ $b$ $(a \neq b)$ の棒を $1$ 本につなぎ, 新たな棒を作る.
これを両端が L 字型の壁を伝うように動かすとき, 棒の継ぎ目はどのような軌跡を描くか.
(有名問題)
答え
長軸, 短軸が $2a,$ $2b$ の楕円の周を対称軸で $4$ 等分した曲線.
解説
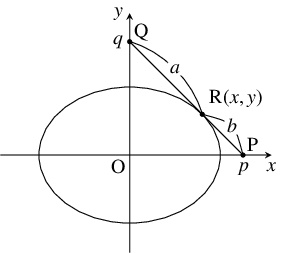
L 字型の壁の隅を原点, 壁を $x$ 軸 $(x \geqq 0),$ $y$ 軸 $(y \geqq 0)$ とする.
新たな棒の一端を $\mathrm P(p,0),$ 他端を $\mathrm Q(0,q),$ 棒の継ぎ目を $\mathrm R(x,y)$ とおき, $\mathrm{PR} = b,$ $\mathrm{QR} = a$ とする.
このとき, $\mathrm{PQ} = a+b$ から,
\[ p^2+q^2 = (a+b)^2 \quad \cdots [1]\]
が成り立つ.
点 $\mathrm R$ は長さが $a+b$ の線分 $\mathrm{PQ}$ を $b:a$ に内分するから,
\[ x = \frac{a}{a+b}p, \quad y = \frac{b}{a+b}q\]
が成り立つ.
よって,
\[ p = \frac{a+b}{a}x, \quad q = \frac{a+b}{b}y \quad \cdots [2]\]
であるから, $[1]$ に $[2]$ を代入すると
\[\frac{(a+b)^2}{a^2}x^2+\frac{(a+b)^2}{b^2}y^2 = (a+b)^2\]
となり, 点 $\mathrm R$ の軌跡の方程式
\[\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1 \quad (x \geqq 0,\ y \geqq 0)\]
が得られる.

クイズ《引きずられた荷物の軌跡》
伸び縮みのしない長さ $1$ のひもの先端に荷物がくくり付けられている.
荷主が $xy$ 平面上の原点 $\mathrm O$ から $x$ 軸正方向へ荷物を引きずりながら移動するとき, 点 $(0,1)$ にあった荷物が描く軌跡はどのような式で表されるか.
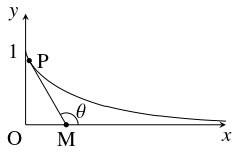
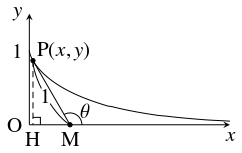
$x \geqq 0$ の範囲で, 荷物が点 $\mathrm P$ にあるとき荷主が点 $\mathrm M$ にいるとして, $x$ 軸正方向と $\mathrm{MP}$ のなす角 $\theta$ を用いて表せ.
(ヒント: 点 $\mathrm P(x,y)$ における曲線の接線の傾き $\dfrac{dy}{dx}$ は直線 $\mathrm{MP}$ の傾きに等しいこと, $x$ は $y = 1$ において連続であることを利用する.)

(有名問題)
答え
$\begin{cases}
x = \cos\theta +\log\tan\dfrac{\theta}{2}, & {} \\
y = \sin\theta & {}
\end{cases} \quad \left(\dfrac{\pi}{2} \leqq \theta < \pi\right)$
解説
- (1)
- $y$ を用いて $\dfrac{dy}{dx}$ を表す.
点 $\mathrm P$ から $x$ 軸に下ろした垂線の足を $\mathrm H$ とおく.
三平方の定理により \[\mathrm{MH} = \sqrt{\mathrm{MP}^2-\mathrm{PH}^2} = \sqrt{1-y^2}\] であるから, \[\frac{dy}{dx} = -\frac{\mathrm{PH}}{\mathrm{MH}} = -\frac{y}{\sqrt{1-y^2}}\] である.
- (2)
- $x$ を $y$ の関数として表す. $x > 0$ のとき. (1) から \[ -\frac{\sqrt{1-y^2}}{y}\frac{dy}{dx} = 1\] であるので, \[\begin{aligned} \int dx &= \int\left( -\frac{\sqrt{1-y^2}}{y}\right)\frac{dy}{dx}\,dx \\ x &= -\int\frac{\sqrt{1-y^2}}{y}\,dy \end{aligned}\] が成り立つ. $u = \sqrt{1-y^2}$ とおく. このとき, $u^2 = 1-y^2$ から \[ y = \sqrt{1-u^2}, \quad \frac{dy}{du} = \frac{-u}{\sqrt{1-u^2}}\] であるので, \[\begin{aligned} x &= -\int\frac{\sqrt{1-y^2}}{y}\frac{dy}{du}\,du \\ &= -\int\frac{u}{\sqrt{1-u^2}}\frac{-u}{\sqrt{1-u^2}}\,du \\ &= \int\frac{u^2}{1-u^2}\,du \\ &= -\int du+\int\frac{du}{1-u^2} \quad (\because u^2 = 1-(1-u^2)) \\ &= -\int du+\frac{1}{2}\left(\int\frac{du}{1+u}+\int\frac{du}{1-u}\right) \\ &\qquad \left(\because\frac{1}{1-u^2} = \frac{1}{2}\left(\frac{1}{1+u}+\frac{1}{1-u}\right)\right) \\ &= -u+\frac{1}{2}\{\log (1+u)-\log (1-u)\} +C \\ &= -u+\frac{1}{2}\log\frac{1+u}{1-u}+C \\ &= -\sqrt{1-y^2}+\frac{1}{2}\log\frac{1+\sqrt{1-y^2}}{1-\sqrt{1-y^2}}+C \\ &= -\sqrt{1-y^2}+\frac{1}{2}\log\frac{(1+\sqrt{1-y^2})^2}{y^2}+C \\ &= -\sqrt{1-y^2}+\log\frac{1+\sqrt{1-y^2}}{y}+C \end{aligned}\] が成り立つ ($C$: 積分定数). ここで, $y = 1$ のとき $x = 0$ であるから, \[ 0 = -\sqrt{1-1^2}+\log\frac{1+\sqrt{1-1^2}}{1}+C\] から $C = 0$ が得られる ($x$ は $y = 1$ において連続であることを用いた). よって, \[ x = -\sqrt{1-y^2}+\log\frac{1+\sqrt{1-y^2}}{y}\] である.
- (3)
- $\theta$ を媒介変数として点 $\mathrm P$ の軌跡を表す. $x \geqq 0$ のとき, $\dfrac{\pi}{2} \leqq \theta < \pi$ であり, \[\sqrt{1-y^2} = \sqrt{1-\sin ^2\theta} = |\cos\theta | = -\cos\theta\] が成り立つから, \[\begin{aligned} x &= \cos\theta +\log\frac{1-\cos\theta}{\sin\theta} \\ &= \cos\theta +\log\frac{2\sin ^2\dfrac{\theta}{2}}{2\sin\dfrac{\theta}{2}\cos\dfrac{\theta}{2}} \\ &= \cos\theta +\log\tan\frac{\theta}{2} \end{aligned}\] である. ゆえに, 点 $\mathrm P$ の軌跡は \[\begin{cases} x = \cos\theta +\log\tan\dfrac{\theta}{2}, & {} \\ y = \sin\theta & {} \end{cases} \quad \left(\frac{\pi}{2} \leqq \theta < \pi\right)\] で表される.
参考
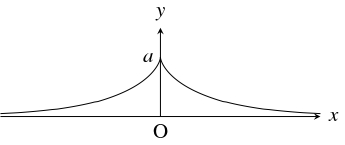
- \[\begin{cases}
x = a\left(\cos\theta +\log\tan\dfrac{\theta}{2}\right), & {} \\
y = a\sin\theta & {}
\end{cases} \quad (0 < \theta < \pi )\]
($a$: 正の数) で定まる曲線を「牽引線」または「トラクトリックス」(tractrix) と呼ぶ.
この曲線は, 媒介変数の取り方を変えれば,
\[\begin{cases}
x = a\left( -\sin t +\log\tan\dfrac{2t+\pi}{4}\right), & {} \\
y = a\cos t & {}
\end{cases} \quad \left( -\frac{\pi}{2} < t < \frac{\pi}{2}\right)\]
で表すこともできる.
- 伸び縮みのしないひもをある図形にたるみなく巻きつけていくとき, またはそれをたるみなくほどいていくとき, ひもの先端が描く軌跡はその図形の「伸開線」または「インボリュート」(involute) と呼ばれる. 「牽引線」は「懸垂線」$y = a\cdot\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}$ ($a$: 正の数) の「伸開線」であることとが知られている.