本格数学クイズ (初等幾何学)
三角形
クイズ《トリチェリーの問題》
$3$ つの工場 A, B, C からなる工業地域に $1$ つの変電所を建てる.
変電所からそれぞれの工場までの送電線の長さの和が最小になるようにするには, 変電所をどのような位置に建てればよいか.
ただし, $\triangle\mathrm{ABC}$ のすべての内角は $120^\circ$ 未満であるとする.
(ヒント: 平面ベクトル $\vec v\,(\neq \vec 0),$ $\vec w$ に対して $|\vec v-\vec w| \geqq |\vec v|-\dfrac{\vec v}{|\vec v|}\cdot\vec w$ が成り立つ.)
(有名問題, 参考: $2000$ 東北大)
答え
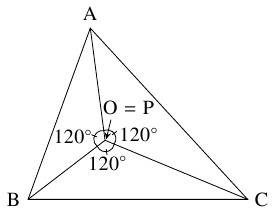
$\angle\mathrm{BPC} = \angle\mathrm{CPA} = \angle\mathrm{APB}$ を満たすような点 $\mathrm P$ ($\triangle\mathrm{ABC}$ と $1$ 辺を共有する正三角形 $\mathrm{BCA}',$ $\mathrm{CAB}',$ $\mathrm{ABC}'$ を $\triangle\mathrm{ABC}$ の外側にかくとき $3$ 直線 $\mathrm{AA}',$ $\mathrm{BB}',$ $\mathrm{CC}'$ の交点).
解説
点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ と異なる点 $\mathrm O$ を基点とする位置ベクトルによって
$\mathrm A(\vec a),$ $\mathrm B(\vec b),$ $\mathrm C(\vec c),$ $\mathrm P(\vec p)$ とおき,
\[ L = |\overrightarrow{\mathrm{PA}}|+|\overrightarrow{\mathrm{PB}}|+|\overrightarrow{\mathrm{PC}}|\]
の最小値を求める.
\[\overrightarrow{e_1} = \frac{\vec a}{|\vec a|}, \quad \overrightarrow{e_2} = \frac{\vec b}{|\vec b|}, \quad \overrightarrow{e_3} = \frac{\vec c}{|\vec c|}\]
とおく.
不等式
\[ |\vec v-\vec w| \geqq |\vec v|-\frac{\vec v}{|\vec v|}\cdot\vec w \quad (\vec v \neq \vec 0) \quad \cdots [\ast ]\]
により,
\[\begin{aligned}
|\overrightarrow{\mathrm{PA}}| &= |\vec a-\vec p| \geqq |\vec a|-\overrightarrow{e_1}\cdot\vec p \quad \cdots [1], \\
|\overrightarrow{\mathrm{PB}}| &= |\vec b-\vec p| \geqq |\vec b|-\overrightarrow{e_2}\cdot\vec p \quad \cdots [2], \\
|\overrightarrow{\mathrm{PC}}| &= |\vec c-\vec p| \geqq |\vec c|-\overrightarrow{e_3}\cdot\vec p \quad \cdots [3]
\end{aligned}\]
が成り立つ.
辺々を加えると,
\[ L \geqq |\vec a|+|\vec b|+|\vec c|-(\overrightarrow{e_1}+\overrightarrow{e_2}+\overrightarrow{e_3})\cdot\vec p\]
が得られる.
\[\overrightarrow{e_1}+\overrightarrow{e_2}+\overrightarrow{e_3} = \vec 0\]
が成り立つように点 $\mathrm O$ をとり直す.
\[ |\overrightarrow{e_1}+\overrightarrow{e_2}| = |-\overrightarrow{e_3}| = |\overrightarrow{e_3}| = 1\]
の両辺を $2$ 乗すると, $|\overrightarrow{e_1}| = |\overrightarrow{e_2}| = 1$ から
\[ 1 = |\overrightarrow{e_1}|^2+2\overrightarrow{e_1}\cdot\overrightarrow{e_2}+|\overrightarrow{e_2}|^2 = 2\overrightarrow{e_1}\cdot\overrightarrow{e_2}+2\]
つまり
\[\overrightarrow{e_1}\cdot\overrightarrow{e_2} = -\dfrac{1}{2}\]
となるので, $\overrightarrow{e_1}$ と $\overrightarrow{e_2}$ のなす角は $120^\circ$ である.
同様に, $\overrightarrow{e_2}$ と $\overrightarrow{e_3},$ $\overrightarrow{e_3}$ と $\overrightarrow{e_1}$ のなす角は $120^\circ$ である.
よって, 上記の点 $\mathrm O$ は
\[\angle\mathrm{BOC} = \angle\mathrm{COA} = \angle\mathrm{AOB}\]
を満たす点として定まる.
しかも, $\triangle\mathrm{ABC}$ の内角に関する条件から, この $\mathrm O$ は $\triangle\mathrm{ABC}$ の内部にとれることに注意する.
このとき,
\[ L \geqq |\vec a|+|\vec b|+|\vec c|\]
が成り立つ.
等号成立は, $[1]$~$[3]$ で等号が成り立つ場合に限る.
これは, $\vec p$ が $\vec a,$ $\vec b,$ $\vec c$ の $1$ 以下の定数倍である場合に限る.
$\vec a,$ $\vec b,$ $\vec c$ は $\vec 0$ でなく互いに平行でないから, これは $\vec p = \vec 0$ の場合である.
ゆえに, $L$ が最小になるような点 $\mathrm P$ は, 上記の点 $\mathrm O$ の位置, つまり $\angle\mathrm{BPC} = \angle\mathrm{CPA} = \angle\mathrm{APB}$ を満たすような位置にある (作図法についてはこちらを参照).
 なお, $[\ast ]$ は, 次のように証明できる: コーシー=シュワルツの不等式により,
\[\begin{aligned}
|\vec v-\vec w| &= \left|\frac{\vec v}{|\vec v|}\right||\vec v-\vec w| \\
&\geqq \left|\frac{\vec v}{|\vec v|}\cdot (\vec v-\vec w)\right| = \left||\vec v|-\dfrac{\vec v}{|\vec v|}\cdot\vec w\right| \quad (\because\vec v\cdot\vec v = |\vec v|^2) \\
&\geqq |\vec v|-\dfrac{\vec v}{|\vec v|}\cdot\vec w
\end{aligned}\]
が成り立つ.
等号成立は, $\vec v-\vec w$ が $\dfrac{\vec v}{|\vec v|}$ の実数倍,つまり $\vec w$ が $\vec v$ の実数倍であって $|\vec v| \geqq \dfrac{\vec v}{|\vec v|}\cdot\vec w$ である場合に限るので, 実数 $l$ に対して
\[\frac{\vec v}{|\vec v|}\cdot l\vec v = l\frac{\vec v\cdot\vec v}{|\vec v|} = l|\vec v|\]
が成り立つことから, $\vec w$ が $\vec v$ の $1$ 以下の実数倍である場合に限る.
なお, $[\ast ]$ は, 次のように証明できる: コーシー=シュワルツの不等式により,
\[\begin{aligned}
|\vec v-\vec w| &= \left|\frac{\vec v}{|\vec v|}\right||\vec v-\vec w| \\
&\geqq \left|\frac{\vec v}{|\vec v|}\cdot (\vec v-\vec w)\right| = \left||\vec v|-\dfrac{\vec v}{|\vec v|}\cdot\vec w\right| \quad (\because\vec v\cdot\vec v = |\vec v|^2) \\
&\geqq |\vec v|-\dfrac{\vec v}{|\vec v|}\cdot\vec w
\end{aligned}\]
が成り立つ.
等号成立は, $\vec v-\vec w$ が $\dfrac{\vec v}{|\vec v|}$ の実数倍,つまり $\vec w$ が $\vec v$ の実数倍であって $|\vec v| \geqq \dfrac{\vec v}{|\vec v|}\cdot\vec w$ である場合に限るので, 実数 $l$ に対して
\[\frac{\vec v}{|\vec v|}\cdot l\vec v = l\frac{\vec v\cdot\vec v}{|\vec v|} = l|\vec v|\]
が成り立つことから, $\vec w$ が $\vec v$ の $1$ 以下の実数倍である場合に限る.

参考
- 分岐点を新たに設けてもよいという条件の下で, 与えられたいくつかの点をもれなく結ぶ最短経路を求める問題は, 「最小シュタイナー木問題」(the shortest path problem) と呼ばれ, インフラの建設計画, 電気回路の設計などに現れる素朴で重要な問題である.
- 同一直線上にある $3$ 点を結ぶ最短経路は, 明らかに最も離れた $2$ 点を結ぶ線分である. よって, $3$ 点の「最小シュタイナー木問題」については, $3$ 点が三角形をなす場合が問題になる. 「三角不等式」$\mathrm P\mathrm P'+\mathrm P'\mathrm P'' \geqq \mathrm P\mathrm P''$ を使うと, これは三角形の各頂点までの距離の和が最小になる点を求める問題に帰着できる (詳細は省略).
- $L$ の最小値を与える点 $\mathrm P$ は $\triangle\mathrm{ABC}$ の「フェルマー点」または「トリチェリ点」(Fermat point, Torricelli point) などと呼ばれる.
- $L$ の最小値 $L_0$ は, $3$ 辺の長さ $a,$ $b,$ $c$ を用いて \[\begin{aligned} L_0 &= \sqrt{\frac{a^2+b^2+c^2+4\sqrt 3S}{2}}, \\ 4S &= \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \end{aligned}\] と表されることが知られている (証明は少し難しい).
クイズ《ナポレオンの定理》
平面おいて $\triangle\mathrm{ABC}$ の外側に正三角形 $\mathrm A'\mathrm{BC},$ $\mathrm B'\mathrm{CA},$ $\mathrm C'\mathrm{AB}$ をかき, それらの重心をそれぞれ $\mathrm A'',$ $\mathrm B'',$ $\mathrm C''$ とおく.
$\triangle\mathrm A''\mathrm B''\mathrm C''$ はどのような形の三角形か.
答え
正三角形.
解説
複素数平面上に $3$ 点 $\mathrm A(\alpha ),$ $\mathrm B(\beta ),$ $\mathrm C(\gamma )$ が反時計回りに並び, 三角形をなしているとする.
- (1)
- $\alpha,$ $\beta,$ $\gamma$ を用いて, 点 $\mathrm A'',$ $\mathrm B'',$ $\mathrm C''$ に対応する複素数 $\alpha'',$ $\beta'',$ $\gamma''$ を表す. 点 $\mathrm A'(\alpha ')$ は点 $\mathrm C(\gamma )$ を中心として点 $\mathrm B(\beta )$ を $\dfrac{\pi}{3}$ だけ回転移動した点であるから, $\zeta = \cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}$ として, \[\begin{aligned} \frac{\alpha '-\gamma}{\beta -\gamma} &= \zeta \\ \alpha '-\gamma &= \zeta (\beta -\gamma ) \\ \alpha ' &= \zeta\beta +(1-\zeta )\gamma \end{aligned}\] である. 点 $\mathrm A''(\alpha '')$ は $\triangle\mathrm A'\mathrm{BC}$ の重心であるから, \[\alpha '' = \frac{\alpha '+\beta +\gamma}{3} = \frac{(1+\zeta )\beta +(2-\zeta )\gamma}{3} \quad \cdots [1]\] である. 同様に, \[\begin{aligned} \beta '' &= \frac{(1+\zeta )\gamma +(2-\zeta )\alpha}{3} \quad \cdots [2], \\ \gamma '' &= \frac{(1+\zeta )\alpha +(2-\zeta )\beta}{3} \quad \cdots [3] \end{aligned}\] である.
- (2)
- $\angle\mathrm B''\mathrm A''\mathrm C''$ に着目して $\triangle\mathrm A''\mathrm B''\mathrm C''$ の形状を調べる. $[1]$~$[3]$ から, \[\begin{aligned} &\frac{\gamma ''-\alpha ''}{\beta ''-\alpha ''} = \frac{3\gamma ''-3\alpha ''}{3\beta ''-3\alpha ''} \\ &= \frac{(1+\zeta )\alpha +(2-\zeta )\beta -(1+\zeta )\beta -(2-\zeta )\gamma}{(1+\zeta )\gamma +(2-\zeta )\alpha -(1+\zeta )\beta -(2-\zeta )\gamma} \\ &= \frac{(1+\zeta )\alpha +(1-2\zeta )\beta +(-2+\zeta )\gamma}{(2-\zeta )\alpha +(-1-\zeta )\beta +(-1+2\zeta )\gamma} \end{aligned}\] が成り立つ. ここで, ド・モアブルの定理により \[\zeta ^3 = \cos\pi +i\sin\pi = -1\] であるから, \[\begin{aligned} \zeta ^3+1 &= 0 \\ (\zeta +1)(\zeta ^2-\zeta +1) &= 0 \end{aligned}\] が成り立つ. $\zeta \neq -1$ つまり $\zeta +1 \neq 0$ であるから, \[\zeta ^2-\zeta +1 = 0\] である. よって, \[\begin{aligned} \zeta (2-\zeta ) &= 2\zeta -\zeta ^2 = 2\zeta -(\zeta -1) = 1+\zeta, \\ \zeta (-1-\zeta ) &= -\zeta -\zeta ^2 = -\zeta -(\zeta -1) = 1-2\zeta, \\ \zeta (-1+2\zeta ) &= -\zeta +2\zeta ^2 = -\zeta +2(\zeta -1) = -2+\zeta \end{aligned}\] であるので, \[\frac{\gamma ''\!-\!\alpha ''}{\beta ''\!-\!\alpha ''} \!=\! \frac{\zeta (2\!-\!\zeta )\alpha\!+\!\zeta (-1\!-\!\zeta )\beta\!+\!\zeta (-1\!+\!2\zeta )\gamma}{(2\!-\!\zeta )\alpha\!+\!(-1\!-\!\zeta )\beta\!+\!(-1\!+\!2\zeta )\gamma} \!=\! \zeta\] が成り立つ. よって, \[\frac{|\gamma ''-\alpha ''|}{|\beta ''-\alpha ''|} = 1, \quad \mathrm{arg}\,\frac{\gamma ''-\alpha ''}{\beta ''-\alpha ''} = \frac{\pi}{3}\] から \[\mathrm A''\mathrm B'' = \mathrm A''\mathrm C'', \quad \angle\mathrm B''\mathrm A''\mathrm C'' = \frac{\pi}{3}\] が成り立つので, $\triangle\mathrm A''\mathrm B''\mathrm C''$ は正三角形である.
参考
- 本問において $\triangle\mathrm A''\mathrm B''\mathrm C''$ が正三角形になることは, ナポレオンによって発見されたといわれ,「ナポレオンの定理」(Napoleon's theorem) として知られている. 正三角形 $\mathrm A''\mathrm B''\mathrm C''$ を $\triangle\mathrm{ABC}$ の「外ナポレオン三角形」 (outer Napoleon triangle) と呼ぶ.
- 余弦定理, 正弦定理, 加法定理による証明については, こちらを参照されたい.
- $\triangle\mathrm{ABC}$ の内側に正三角形 $\mathrm A'\mathrm{BC},$ $\mathrm B'\mathrm{CA},$ $\mathrm C'\mathrm{AB}$ をかいても, それらの重心を結ぶ三角形 $\mathrm A''\mathrm B''\mathrm C''$ は正三角形になることが, 上記と同様に証明できる ($\zeta$ を $\cos\left( -\dfrac{\pi}{3}\right) +i\sin\left( -\dfrac{\pi}{3}\right)$ に置き換える). このことも「ナポレオンの定理」として知られている. この場合の正三角形 $\mathrm A''\mathrm B''\mathrm C''$ を $\triangle\mathrm{ABC}$ の「内ナポレオン三角形」 (inner Napoleon triangle) と呼び,「内ナポレオン三角形」「外ナポレオン三角形」をまとめて「ナポレオン三角形」と呼ぶ.
- 「ナポレオン三角形」の重心はもとの三角形の重心に一致することが知られている.
- $2$ つの「ナポレオン三角形」の面積の差はもとの三角形の面積に等しいことが知られている.
- 「ナポレオン三角形」$\mathrm A''\mathrm B''\mathrm C''$ ともとの三角形 $\mathrm{ABC}$ の頂点を結ぶ $3$ 直線 $\mathrm{AA}'',$ $\mathrm{BB}'',$ $\mathrm{CC}''$ は $1$ 点で交わることが知られている. この点を $\triangle\mathrm{ABC}$ の「ナポレオン点」(outer/inner Napoleon point) と呼ぶ.
円
クイズ《レギオモンタヌスの問題》
フィールドの中央から $d$ だけ離れたセンターライン上の地点から, 選手が敵陣のゴールラインに向かって真っすぐ進んでいる.
ゴールの幅が $w$ であるとき, ゴールを見込む角が最大になるという意味でシュートを放つのに最も適しているのは, ゴールラインからどれだけ離れた地点か.
ただし, $d > \dfrac{w}{2}$ とする.
(有名問題)
答え
$\sqrt{\left( d+\dfrac{w}{2}\right)\left(d-\dfrac{w}{2}\right)}$ だけ離れた地点.
解説
ゴールラインと選手が進む直線の交点を $\mathrm O,$ ゴールの両端を $\mathrm A,$ $\mathrm B$ とおき, 点 $\mathrm P$ でゴールを見込む角 $\angle\mathrm{APB}$ が最大になるとする.
$\mathrm A,$ $\mathrm B$ を通って直線 $\mathrm{OP}$ に点 $\mathrm T$ で接する円周 $C$ をかく.
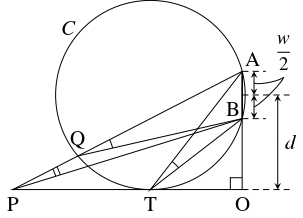 $\mathrm P \neq \mathrm T$ のときは線分 $\mathrm{AP}$ と $C$ の交点を $\mathrm Q$ とおくと
\[\angle\mathrm{APB} < \angle\mathrm{AQB} = \angle\mathrm{ATB}\]
となってしまうから, $\mathrm P = \mathrm T$ である.
よって, 方べきの定理により
\[\mathrm{OP}^2 = \mathrm{OA}\cdot\mathrm{OB}\]
であるから, ゴールを見込む角が最も大きくなる地点のゴールラインからの距離は
\[\mathrm{OP} = \sqrt{\mathrm{OA}\cdot\mathrm{OB}} = \sqrt{\left( d+\frac{w}{2}\right)\left(d-\frac{w}{2}\right)}\]
である.
$\mathrm P \neq \mathrm T$ のときは線分 $\mathrm{AP}$ と $C$ の交点を $\mathrm Q$ とおくと
\[\angle\mathrm{APB} < \angle\mathrm{AQB} = \angle\mathrm{ATB}\]
となってしまうから, $\mathrm P = \mathrm T$ である.
よって, 方べきの定理により
\[\mathrm{OP}^2 = \mathrm{OA}\cdot\mathrm{OB}\]
であるから, ゴールを見込む角が最も大きくなる地点のゴールラインからの距離は
\[\mathrm{OP} = \sqrt{\mathrm{OA}\cdot\mathrm{OB}} = \sqrt{\left( d+\frac{w}{2}\right)\left(d-\frac{w}{2}\right)}\]
である.

クイズ《正多角形の辺と対角線の長さの総和》
ペンキで正 $n$ 角形の周とそのすべての対角線を描くとき, 周のみを描くときの何倍のペンキを使うか.
(有名問題)
答え
$\dfrac{1}{4\sin ^2\dfrac{\pi}{2n}}$ 倍.
解説
$1$ 辺の長さが $1$ の正 $n$ 角形 $\mathrm P_0\mathrm P_1\cdots\mathrm P_{n-1}$ において, 辺と対角線の長さの総和 $L$ を求める.
$a_k = \mathrm P_0\mathrm P_k$ $(1 \leqq k \leqq n-1)$ とおく.
四角形 $\mathrm P_0\mathrm P_1\mathrm P_k\mathrm P_{n-1}$ $(2 \leqq k \leqq n-2)$ に「トレミーの定理」を適用すると, $\mathrm P_0\mathrm P_1 = \mathrm P_0\mathrm P_{n-1} = a_1,$ $\mathrm P_1\mathrm P_k = a_{k-1},$ $\mathrm P_{n-1}\mathrm P_k = a_{n-k-1},$ $\mathrm P_1\mathrm P_{n-1} = a_2,$ $\mathrm P_0\mathrm P_k = a_k$ から
\[ a_1a_{k-1}+a_1a_{n-k-1} = a_2a_k\]
が得られる.
これらの辺々と
\[ 2a_1a_{n-2}+2a_1a_{n-1} = a_2a_1+a_2a_{n-1}+2a_1{}^2\]
を加えると,
\[\begin{aligned}
2a_1\sum_{k = 1}^{n-1}a_k &= 2a_1{}^2+a_2\sum_{k = 1}^{n-1}a_k \\
(2a_1-a_2)\sum_{k = 1}^{n-1}a_k &= 2a_1{}^2 \\
\sum_{k = 1}^{n-1}a_k &= \frac{2a_1{}^2}{2a_1-a_2}
\end{aligned}\]
が得られる.
よって,
\[ L = \frac{1}{2}\sum_{j = 0}^{n-1}\sum_{k = 0}^{n-1}\mathrm P_j\mathrm P_k = \frac{n}{2}\sum_{k = 0}^{n-1}\mathrm P_0\mathrm P_k = \frac{n}{2}\sum_{k = 1}^{n-1}a_k = \frac{a_1{}^2n}{2a_1-a_2}\]
が成り立つ.
ここで, $a_1 = 1$ であり, 頂角の大きさが $\dfrac{n-2}{n}\pi$ の二等辺三角形 $\mathrm P_0\mathrm P_1\mathrm P_2$ を半分にした直角三角形に着目すると
\[ a_2 = 2\sin\dfrac{n-2}{2n}\pi = 2\sin\left(\frac{\pi}{2}-\frac{\pi}{n}\right) = 2\cos\frac{\pi}{n}\]
であることがわかるから,
\[ L = \frac{n}{2-a_2} = \frac{n}{2\left( 1-\cos\dfrac{\pi}{n}\right)} = \frac{n}{4\sin ^2\dfrac{\pi}{2n}}\]
である.
ゆえに, 求める倍率は, \[ L\div n = \frac{1}{4\sin ^2\dfrac{\pi}{2n}}\] である.
ゆえに, 求める倍率は, \[ L\div n = \frac{1}{4\sin ^2\dfrac{\pi}{2n}}\] である.
クイズ《正七角形調和》
正七角形 $\mathrm{ABCDEFG}$ の形をした公園があり, 各頂点から他の頂点に向かって真っすぐな歩道が伸びている.
B さん, C さんがそれぞれ点 $\mathrm B,$ $\mathrm C$ から点 $\mathrm G$ に向かって真っすぐに歩いたところ, 所要時間は同じになった.
A さんが B さん, C さんの平均の速さで点 $\mathrm A$ から点 $\mathrm G$ に向かって真っすぐに歩くとき, 所要時間は B さんの何倍になるか.
(オリジナル)
答え
$\dfrac{1}{2}$ 倍.
解説
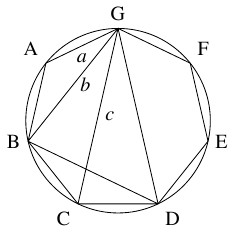
正七角形 $\mathrm{ABCDEFG}$ において, $a = \mathrm{GA},$ $b = \mathrm{GB},$ $c = \mathrm{GC}$ とおく.
B さん, C さんの所要時間を $1$ とし, B さん, C さんの平均の速さ (行き $\dfrac{1}{b},$ 帰り $\dfrac{1}{c}$ の速さで片道の距離 $1$ の道のりを往復するときの速さ) を $v$ とおく.
- (1)
- B さん, C さんの速さはそれぞれ $\dfrac{1}{b},$ $\dfrac{1}{c}$ であるから, \[ v = \frac{2}{\dfrac{1}{b}+\dfrac{1}{c}}\] である.
- (2)
- 四角形 $\mathrm{BCDG}$ は円に内接するから,「トレミーの定理」により,
\[\mathrm{BC}\cdot\mathrm{DG}+\mathrm{CD}\cdot\mathrm{GB} = \mathrm{BD}\cdot\mathrm{CG}\]
つまり
\[ ac+ab = bc\]
が成り立つ.
両辺を $abc$ で割ると, \[\frac{1}{b}+\frac{1}{c} = \frac{1}{a}\] が得られる. よって, \[ v = 2\div\frac{1}{a} = 2a\] である.
- (3)
- ゆえに, A さんの所要時間は
\[\frac{a}{v} = \frac{a}{2a} = \frac{1}{2}\]
であり, これは B さんの所要時間の
である.$\dfrac{1}{2}\div 1 = \dfrac{1}{2}$ (倍)
参考
正七角形の $1$ 辺の長さ $a$ と対角線の長さ $b,$ $c$ に関する関係式 $a^{-1} = b^{-1}+c^{-1}$ は「正七角形調和」として知られている.