本格数学クイズ (確率論)
確率に関する問題でも, 組合せ論的な意味合いが強い問題は「本格数学クイズ (組合せ論)」のページに掲載しています.
反復試行の確率
クイズ《ド・メレの $2$ つのさいころ》
$1$ つのさいころを $4$ 回ふって $6$ の目が出れば勝ちというゲーム A と, $2$ つのさいころを $24$ 回ふって $6$ のぞろ目が出れば勝ちというゲーム B は, どちらの方が勝つ確率が高いか.
(ヒント: $\log_{10}2 < 0.3011,$ $\log_{10}3 < 0.4772,$ $\log_{10}7 > 0.8450$ であることを使う.)
(有名問題)
答え
A.
解説
$1$ つのさいころを $4$ 回ふって $6$ の目が少なくとも $1$ 回出る確率 $p$ は, $6$ 以外の目が $4$ 回続けて出るという事象の余事象の確率であり,
\[ p = 1-\left(\dfrac{5}{6}\right) ^4\]
である.
また, $2$ つのさいころを $24$ 回ふるとき, $6$ のぞろ目が少なくとも $1$ 回出る確率 $q$ は, $6$ のぞろ目以外の目が $24$ 回続けて出るという事象の余事象の確率であり, \[ q = 1-\left(\dfrac{35}{36}\right) ^{24}\] である. \[ p-q = \left(\dfrac{35}{36}\right) ^{24}-\left(\dfrac{5}{6}\right) ^4\] であるから, $\log_{10}\left(\dfrac{35}{36}\right) ^{24},$ $\log_{10}\left(\dfrac{5}{6}\right) ^4$ の大小関係を調べる. \[\begin{aligned} &\log_{10}\left(\frac{35}{36}\right) ^{24}-\log_{10}\left(\frac{5}{6}\right) ^4 \\ &= 24\log_{10}\frac{35}{36}-4\log_{10}\frac{5}{6} \\ &= 24\log_{10}\frac{5\cdot 7}{2^2\cdot 3^2}-4\log_{10}\frac{5}{2\cdot 3} \\ &= 24\log_{10}\frac{10\cdot 7}{2^3\cdot 3^2}-4\log_{10}\frac{10}{2^2\cdot 3} \\ &= 24\left( 1-3\log_{10}2-2\log_{10}3+\log_{10}7\right) \\ &\qquad -4(1-2\log_{10}2-\log_{10}3) \\ &= 20-64\log_{10}2-44\log_{10}3+24\log_{10}7 \\ &> 20-64\cdot 0.3011-44\cdot 0.4772+24\cdot 0.8450 \\ &= 0.0128 \\ &> 0 \end{aligned}\] であるから, \[\log_{10}\left(\frac{35}{36}\right) ^{24} > \log_{10}\left(\frac{5}{6}\right) ^4\] である. よって, $\left(\dfrac{35}{36}\right) ^{24} > \left(\dfrac{5}{6}\right) ^4$ つまり $p-q > 0$ であるから, $p > q$ である.
また, $2$ つのさいころを $24$ 回ふるとき, $6$ のぞろ目が少なくとも $1$ 回出る確率 $q$ は, $6$ のぞろ目以外の目が $24$ 回続けて出るという事象の余事象の確率であり, \[ q = 1-\left(\dfrac{35}{36}\right) ^{24}\] である. \[ p-q = \left(\dfrac{35}{36}\right) ^{24}-\left(\dfrac{5}{6}\right) ^4\] であるから, $\log_{10}\left(\dfrac{35}{36}\right) ^{24},$ $\log_{10}\left(\dfrac{5}{6}\right) ^4$ の大小関係を調べる. \[\begin{aligned} &\log_{10}\left(\frac{35}{36}\right) ^{24}-\log_{10}\left(\frac{5}{6}\right) ^4 \\ &= 24\log_{10}\frac{35}{36}-4\log_{10}\frac{5}{6} \\ &= 24\log_{10}\frac{5\cdot 7}{2^2\cdot 3^2}-4\log_{10}\frac{5}{2\cdot 3} \\ &= 24\log_{10}\frac{10\cdot 7}{2^3\cdot 3^2}-4\log_{10}\frac{10}{2^2\cdot 3} \\ &= 24\left( 1-3\log_{10}2-2\log_{10}3+\log_{10}7\right) \\ &\qquad -4(1-2\log_{10}2-\log_{10}3) \\ &= 20-64\log_{10}2-44\log_{10}3+24\log_{10}7 \\ &> 20-64\cdot 0.3011-44\cdot 0.4772+24\cdot 0.8450 \\ &= 0.0128 \\ &> 0 \end{aligned}\] であるから, \[\log_{10}\left(\frac{35}{36}\right) ^{24} > \log_{10}\left(\frac{5}{6}\right) ^4\] である. よって, $\left(\dfrac{35}{36}\right) ^{24} > \left(\dfrac{5}{6}\right) ^4$ つまり $p-q > 0$ であるから, $p > q$ である.
参考
フランスの数学者パスカルは, 貴族のド・メレから,
ド・メレは誤って, $1$ つのさいころを $4$ 回ふったとき $6$ の目が出る確率は $1$ 回ふって $6$ の目が出る確率 $\dfrac{1}{6}$ の $4$ 倍の $4\cdot\dfrac{1}{6} = \dfrac{2}{3}$ で, $2$ つのさいころを $24$ 回ふったとき $6$ のぞろ目が出る確率は $1$ 回ふって $6$ のぞろ目が出る確率 $\dfrac{1}{36}$ の $24$ 倍の $24\cdot\dfrac{1}{36} = \dfrac{2}{3}$ であると考えた.
パスカルは, 出る確率から計算するのではなく, 出ない確率から計算するのだと指摘した. つまり, 前者のゲームで勝つ確率は $1-\left(\dfrac{5}{6}\right) ^4 = 0.51774\cdots > 0.5$ で, 後者のゲームで勝つ確率は $1-\left(\dfrac{35}{36}\right) ^{24} = 0.49140\cdots < 0.5$ である.
上記の質問は, 確率論の起源になった問題の $1$ つであり,「ド・メレの $2$ つのさいころ」として知られている.
- $1$ つのさいころを $4$ 回ふって $6$ の目が出れば勝ち
- $2$ つのさいころを $24$ 回ふって $6$ のぞろ目が出れば勝ち
ド・メレは誤って, $1$ つのさいころを $4$ 回ふったとき $6$ の目が出る確率は $1$ 回ふって $6$ の目が出る確率 $\dfrac{1}{6}$ の $4$ 倍の $4\cdot\dfrac{1}{6} = \dfrac{2}{3}$ で, $2$ つのさいころを $24$ 回ふったとき $6$ のぞろ目が出る確率は $1$ 回ふって $6$ のぞろ目が出る確率 $\dfrac{1}{36}$ の $24$ 倍の $24\cdot\dfrac{1}{36} = \dfrac{2}{3}$ であると考えた.
パスカルは, 出る確率から計算するのではなく, 出ない確率から計算するのだと指摘した. つまり, 前者のゲームで勝つ確率は $1-\left(\dfrac{5}{6}\right) ^4 = 0.51774\cdots > 0.5$ で, 後者のゲームで勝つ確率は $1-\left(\dfrac{35}{36}\right) ^{24} = 0.49140\cdots < 0.5$ である.
上記の質問は, 確率論の起源になった問題の $1$ つであり,「ド・メレの $2$ つのさいころ」として知られている.
クイズ《賞金の分配問題》
$2$ 人で公平な勝負を繰り返し, 先に $3$ 回勝った方が賞金をすべてもらうというゲームを A が $2$ 勝, B が $1$ 勝の段階で中止するとき, 賞金はどのような割合で A, B に分配するべきか.
(有名問題)
答え
$3:1$ の割合に分配する.
解説
勝負が決まるまで続けるとき,
\[ \left(\frac{1}{2}\right) ^2 = \frac{1}{4}\]
の確率で B が勝ち,
\[ 1-\frac{1}{4} = \frac{3}{4}\]
の確率で A が勝つから, 賞金は
\[\frac{3}{4}:\frac{1}{4} = 3:1\]
の割合で分配するべきである
参考
本問は, ド・メレからパスカルへ出された, 確率論誕生のきっかけとなった質問の $1$ つを厳密化したものである.
同様の問題が, それ以前にルカ・パチョーリの著書『スムマ』($1494$ 年) に記されている.
反復試行の確率
クイズ《コイン投げの確率の最大値》
表, 裏が等確率で出る $1$ 枚のコインがある.
これをちょうど $r$ 回表が出る確率が最大となるような回数だけ投げるとき, 何回投げればよいか.
(有名問題)
答え
$2r-1$ 回, または $2r$ 回.
解説
コインを $n$ 回投げて $r$ 回表が出る確率を $p_n$ とおく.
\[\begin{aligned}
\frac{p_{n+1}}{p_n} &= \frac{{}_{n+1}\mathrm C_r\left(\dfrac{1}{2}\right) ^r\left(\dfrac{1}{2}\right) ^{n+1-r}}{{}_n\mathrm C_r\left(\dfrac{1}{2}\right) ^r\left(\dfrac{1}{2}\right) ^{n-r}} \\
&= \frac{1}{2}\cdot\frac{(n+1)!}{r!(n+1-r)!}\div\frac{n!}{r!(n-r)!} \\
&= \frac{n+1}{2(n+1-r)}
\end{aligned}\]
であるから,
\[\begin{aligned}
p_{n+1} > p_n &\iff \frac{p_{n+1}}{p_n} > 1 \\
&\iff \frac{n+1}{2(n+1-r)} > 1 \\
&\iff n+1 > 2(n+1-r) \\
&\iff n < 2r-1, \\
p_{n+1} = p_n &\iff n = 2r-1, \\
p_{n+1} < p_n &\iff n > 2r-1
\end{aligned}\]
が成り立つ.
よって,
\[ p_1 < \cdots < p_{2r-1} = p_{2r} > p_{2r+1} > \cdots\]
であるから, $p_n$ は $n = 2r-1,$ $2r$ のとき最大となる.
条件付き確率, 確率の乗法定理
クイズ《モンティ・ホール問題》
$3$ つのドア A, B, C のうち, いずれかのドアの向こうに賞品が無作為に隠されている.
挑戦者はドアを $1$ つだけ開けて, 賞品があれば, それをもらうことができる.
挑戦者がドアを選んでからドアを開けるまでの間に, 司会者は残った $2$ つのドアのうち, はずれのドアを $1$ つ無作為に開ける.
このとき, 挑戦者は開けるドアを変更することができる.
ドアを変更するとき, しないときのどちらが賞品を得る確率が高いか.
(有名問題)
答え
ドアを変更するとき.
解説
ドア A, B, C の向こうに賞品があるという事象をそれぞれ $A,$ $B,$ $C$ とおく.
さらに, 挑戦者が A を選んだとき, 司会者が C を開けるという事象を $E$ とおく.
司会者が C を開けたとき, A が当たりである条件付き確率 $P_E(A),$ B が当たりである条件付き確率 $P_E(B)$ の大小を比較すればよい.
- (1)
- まず, $P(E)$ を求める.
賞品は無作為に隠されているから,
\[ P(A) = P(B) = P(C) = \frac{1}{3}\]
である.
- A が当たりのとき司会者は C の他に B も開けることができるから, $P_A(E) = \dfrac{1}{2}$ であり, \[ P(A\cap E) = P(A)P_A(E) = \frac{1}{3}\cdot\dfrac{1}{2} = \frac{1}{6} \quad \cdots [1]\] である.
- B が当たりのとき司会者は C を開けるしかないから, $P_B(E) = 1$ であり, \[ P(B\cap E) = P(B)P_B(E) = \frac{1}{3}\cdot 1 = \frac{1}{3} \quad \cdots [2]\] である.
- C が当たりのとき司会者は C を開けることはないから, $P_C(E) = 0$ であり, \[ P(C\cap E) = P(C)P_C(E) = \frac{1}{3}\cdot 0 = 0\] である.
- (2)
- 次に, $P_E(A),$ $P_E(B)$ の各値を求めて比較する.
- $[1]$ から, \[ P_E(A) = \frac{P(A\cap E)}{P(E)} = \frac{1}{6}\div\frac{1}{2} = \frac{1}{3}\] である.
- $[2]$ から, \[ P_E(B) = \frac{P(B\cap E)}{P(E)} = \frac{1}{3}\div\frac{1}{2} = \frac{2}{3}\] である.
参考
- 本問は, アメリカのテレビ番組 “Let's make a deal” の中で行われたゲームに由来をもち, その司会者の名に因んで「モンティ・ホール問題」 (Monty Hall problem) と呼ばれる.
- 全事象が互いに排反な事象 $A_1,$ $\cdots,$ $A_n$ に分けられるとき,「全確率の定理」(theorem of total probability) \[\begin{aligned} P(E) &= P(A_1\cap E)+\cdots +P(A_n\cap E) \\ &= P(A_1)P_{A_1}(E)+\cdots +P(A_n)P_{A_n}(E) \end{aligned}\] が成り立つ.
- (2) で導いた等式 \[ P_E(A) = \dfrac{P(A)P_A(E)}{P(E)}\] は, 「ベイズの定理」(Bayes' theorem) として知られている.
- 「モンティ・ホール問題」によく似た「$3$ 囚人の問題」「ベルトランの箱の問題」も有名である.
クイズ《ホイヘンスの第 $2$ 問題》
袋の中に赤玉が $a$ 個, 白玉が $b$ 個入っている.
あるクラスの生徒 $n$ 人が玉を $1$ 個取り出して戻すという操作を誰かが赤玉を取り出すまで出席番号順に何巡でも繰り返すとき, $k$ 番の生徒が赤玉を取り出す確率はいくらか.
(有名問題)
答え
$\dfrac{ab^{k-1}(a+b)^{n-k}}{(a+b)^n-b^n}.$
解説
$k$ 番の生徒が赤玉を取り出す確率を $p_k$ とおき,
\[\alpha = \frac{a}{a+b}, \quad \beta = \frac{b}{a+b}\]
とおく.
となる.
これを $[3]$ に代入すると,
\[\begin{aligned}
p_k &= \frac{\alpha\beta ^{k-1}}{1-\beta ^n} \\
&= \frac{a}{a+b}\cdot\frac{b^{k-1}}{(a+b)^{k-1}}\div\left\{ 1-\frac{b^n}{(a+b)^n}\right\} \\
&= \frac{ab^{k-1}(a+b)^{n-k}}{(a+b)^n-b^n}
\end{aligned}\]
が得られる.
- (i)
- 最初に $1$ 番の生徒が赤玉を取り出すとき. その確率は $\alpha$ である.
- (ii)
- 最初に $1$ 番の生徒が白玉を取り出すとき. $1$ 番の生徒は $2$ 番の生徒から始めたときの $n$ 番目と見なせるから, $1$ 番の生徒が赤玉を取り出す確率は $\beta p_n$ である.
| $p_1 = \alpha +p_1\beta ^n$ よって $p_1 = \dfrac{\alpha}{1-\beta ^n}$ |
参考
本問は「ホイヘンスの第 $2$ 問題」(Huygens' second problem) として知られている.
クイズ《$n$ 回以下のじゃんけんで順位が決まる確率》
$3$ 人がじゃんけんをして, $n$ 回以下で $1$ 位から $3$ 位までの順位が決まる確率はいくらか.
ただし, $3$ 人の手の出し方は, どれも同様に確からしいとする.
(有名問題)
答え
$\dfrac{3^n-2n-1}{3^n}.$
解説
- (1)
- $3$ 人がじゃんけんをして, ちょうど $n$ 回目で $1$ 位から $3$ 位までの順位が決まる確率 $p_n$ を求める.
$n \geqq 2$ のとき, ちょうど $n$ 回目で $1$ 位から $3$ 位までの順位が決まるのは,
$1 \leqq k \leqq n-1$ なるある整数 $k$ に対して, 次の条件が成り立つ場合である.
- $1$ 回目から $k-1$ 回目まで $3$ 人があいこである.
- $k$ 回目に $3$ 人があいこにならない.
- $k+1$ 回目から $n-1$ 回目まで残った $2$ 人があいこである.
- $n$ 回目に残った $2$ 人があいこにならない.
- (2)
- $3$ 人がじゃんけんをして, $n$ 回以下で $1$ 位から $3$ 位までの順位が決まる確率 $S_n = p_1+\cdots +p_n$ を求める.
$\qquad S_n = 0+\dfrac{4}{9}+\dfrac{8}{27}+\cdots +\dfrac{4(n-1)}{3^n}$
の辺々に $\dfrac{1}{3}$ をかけると,
$\quad\,\dfrac{1}{3}S_n = \qquad\ \!0+\dfrac{4}{27}+\cdots +\dfrac{4(n-2)}{3^n}+\dfrac{4(n-1)}{3^{n+1}}$
となる. 辺々を引くと
$\begin{aligned} \quad\frac{2}{3}S_n &= \qquad\!\!\frac{4}{9}+\frac{4}{27}+\cdots +\frac{4}{3^n}-\frac{4(n-1)}{3^{n+1}} \\ &= \frac{4}{9}\cdot\frac{1-\left(\dfrac{1}{3}\right) ^{n-1}}{1-\dfrac{1}{3}}-\frac{4(n-1)}{3^{n+1}} \\ &= \frac{2}{3}\left\{ 1-\frac{1}{3^{n-1}}-\frac{2(n-1)}{3^n}\right\} \\ &= \frac{2}{3}\cdot\frac{3^n-2n-1}{3^n} \end{aligned}$
となるので, \[ S_n = \frac{3^n-2n-1}{3^n}\] である.
クイズ《誕生日が一致する確率》
公転周期が $n$ 日の惑星で集会を開く.
同じ誕生日の人がいる確率が $2$ 分の $1$ 以上になるのは, この惑星の住人が何人以上集まったときか.
$x$ が十分に小さいとき近似式 $1-x \fallingdotseq e^{-x}$ ($e$: ネイピア数), $a^{x(x-1)} \fallingdotseq a^{x^2}$ $(0 < a < 1)$ が成り立つことを利用して解け.
(有名問題)
答え
約 $\sqrt{2\log 2}\sqrt n$ 人以上 (約 $1.17741\sqrt n$ 人以上).
解説
集会の参加者が $r$ 人であるとする.
この中に同じ誕生日の人がいない確率は
\[\begin{aligned}
&\frac{n-1}{n}\cdot\frac{n-2}{n}\cdot\cdots\cdot\frac{n-(r-1)}{n} \\
&= \left( 1-\frac{1}{n}\right)\left( 1-\frac{2}{n}\right)\cdots\left( 1-\frac{r-1}{n}\right) \\
&\fallingdotseq e^{-\frac{1}{n}}e^{-\frac{2}{n}}\cdots e^{-\frac{r-1}{n}} \\
&= e^{-\frac{1+2+\cdots +(r-1)}{n}} = e^{-\frac{r(r-1)}{2n}} \\
&\fallingdotseq e^{-\frac{r^2}{2n}}
\end{aligned}\]
であるから, 同じ誕生日の人がいる確率はおよそ
\[ 1-e^{-\frac{r^2}{2n}}\]
である.
この値が $\dfrac{1}{2}$ 以上になる条件は,
\[\begin{aligned}
1-e^{-\frac{r^2}{2n}} &\geqq \frac{1}{2} \\
e^{-\frac{r^2}{2n}} &\leqq \frac{1}{2} \\
-\frac{r^2}{2n} &\leqq \log\frac{1}{2} = -\log 2 \\
r^2 &\geqq 2\log 2\cdot n \\
r &\geqq \sqrt{2\log 2}\sqrt n
\end{aligned}\]
である.
参考
$n = 365$ のとき, 同じ誕生日の人がいる確率が $\dfrac{1}{2}$ 以上になる人数は $23$ 人以上である.
クイズ《ポリアの壺》
最初, 壺の中に色 $1$ の玉が $a_1$ 個, $\cdots,$ 色 $r$ の玉が $a_r$ 個だけ入っている.
壺の中から無作為に玉を $1$ 個取り出して, その玉と同じ色の玉を $c$ 個だけ壺の中に入れ, 取り出した玉も戻すという試行を繰り返す.
$n$ 回目に色 $i$ $(1 \leqq i \leqq r)$ の玉を取り出す確率はいくらか.
(有名問題)
答え
$\dfrac{a_i}{a_1+\cdots +a_r}.$
解説
$n$ 回目に色 $i$ $(1 \leqq i \leqq r)$ の玉を取り出す確率を $p_n$ とおく.
\[ p_n = \frac{a_i}{a_1+\cdots +a_r} \quad \cdots [*]\]
であることを数学的帰納法で示す.
- (i)
- $n = 1$ のとき. 明らかに $[*]$ が成り立つ.
- (ii)
- $n = k$ ($k$: 正の整数) のとき $[*]$ が成り立つとする. また, $k$ 回目の試行を行う直前の壺の中にある色 $i$ の玉の個数を $x,$ その他の色の玉の個数を $y$ とおく. $k$ 回目に取り出す玉の色で場合に分けて考えると, \[\begin{aligned} p_{k+1} &= p_k\cdot\frac{x+c}{x+y+c}+(1-p_k)\cdot\frac{x}{x+y+c} \\ &= \frac{x}{x+y}\cdot\frac{x+c}{x+y+c}+\frac{y}{x+y}\cdot\frac{x}{x+y+c} \\ &= \frac{x(x+y+c)}{(x+y)(x+y+c)} = \frac{x}{x+y} \\ &= p_k = \frac{a_i}{a_1+\cdots +a_r} \end{aligned}\] が得られる. よって, $n = k+1$ のとき $[*]$ が成り立つ.
参考
- 確率変数が時間的に変化するような確率のモデルは「確率過程」(stochastic process) と呼ばれる.
- 本問は「ポリアの壺問題」(Polya's urn problem) として有名である.
クイズ《破産の確率》
A は $m$ 個, B は $n$ 個のあめを持っている.
$2$ 人はゲームを行い, 勝者が敗者から $1$ 個のあめをもらうという試行を, 一方のあめがなくなるまで繰り返す.
各回のゲームで A の勝率が $a,$ B の勝率が $b$ $(0 < a \leqq b < 1)$ であり, 引き分けはないとするとき, B のあめがなくなる確率はいくらか.
(有名問題)
答え
$a = b$ のとき $\dfrac{m}{m+n},$ $a < b$ のとき $\dfrac{a^n(b^m-a^m)}{b^{m+n}-a^{m+n}}.$
解説
B のあめが $k$ 個になったときに最終的に B のあめがなくなる確率を $p_k$ とおく.
B のあめが $k$ 個 $(k \geqq 1)$ のとき,
確率 $a$ でゲームに負けてあめが $k-1$ 個になり,
確率 $b$ でゲームに勝ってあめが $k+1$ 個になるから,
\[ p_k = ap_{k-1}+bp_{k+1} \quad \cdots [*]\]
が成り立つ.
- (i)
- $a = b$ のとき. $[*]$ に $a = b = \dfrac{1}{2}$ を代入して整理すると \[ p_{k+1}-2p_k+p_{k-1} = 0\] となる. よって, \[ p_{k+1}-p_k = p_k-p_{k-1} \quad (k \geqq 1)\] が成り立つので, $\{ p_k\}$ は等差数列である. $p_0 = 1,$ $p_{m+n} = 0$ であるから, その公差は $c = -\dfrac{1}{m+n}$ である. ゆえに, 求める確率は \[ p_n = p_0+cn = 1-\frac{n}{m+n} = \frac{m}{m+n}\] である.
- (ii)
- $a < b$ のとき. $[*]$ を整理すると \[ p_{k+1}-\frac{1}{b}p_k+\frac{a}{b}p_{k-1} = 0\] となる. よって, \[ p_{k+1}-p_k = \frac{a}{b}(p_k-p_{k-1}) \quad (k \geqq 1)\] が成り立つので, $\{ p_{k+1}-p_k\}$ は第 $0$ 項 $c,$ 公比 $\dfrac{a}{b}$ の等比数列であり, その一般項は \[ p_{k+1}-p_k = c\left(\frac{a}{b}\right) ^k\] である. したがって, \[\begin{aligned} 0 &= p_{m+n} = p_0+\sum_{k = 0}^{m+n-1}c\left(\frac{a}{b}\right) ^k = 1+c\cdot\frac{1-\dfrac{a^{m+n}}{b^{m+n}}}{1-\dfrac{a}{b}} \\ c &= -\frac{1-\dfrac{a}{b}}{1-\dfrac{a^{m+n}}{b^{m+n}}} \end{aligned}\] である. ゆえに, 求める確率は \[\begin{aligned} p_n &= p_0+\sum_{k = 0}^{n-1}c\left(\frac{a}{b}\right) ^k = 1-\frac{1-\dfrac{a}{b}}{1-\dfrac{a^{m+n}}{b^{m+n}}}\cdot\frac{1-\dfrac{a^n}{b^n}}{1-\dfrac{a}{b}} \\ &= 1-\frac{b^{m+n}-a^nb^m}{b^{m+n}-a^{m+n}} = \frac{a^n(b^m-a^m)}{b^{m+n}-a^{m+n}} \end{aligned}\] である.
クイズ《くじ引きのサドンデス》
つぼの中に赤玉, 白玉を入れ, $2$ 人が交互に玉を $1$ 個ずつ取り出して, 先に赤玉を取り出した者を勝者とするゲームを行う.
どのように赤玉, 白玉を入れれば先手, 後手の勝率が等しくなるか.
ただし, 取り出した玉は, もとに戻さないものとする.
(参考: $1984$ 京都大)
答え
赤玉を $1$ 個, 白玉を奇数個入れる.
解説
-
赤玉の個数を $r,$ 白玉の個数を $s$ とおき, 先手が勝つ確率を $P(A),$ 後手が勝つ確率を $P(B)$ とおく.
ちょうど $k$ 回目 (つまり $2$ 人の取り出した玉の合計がちょうど $k$ 個になったとき) に勝者が決まる確率を $p_k$ とおく.
- (1)
- $P(A),$ $P(B)$ を $p_k$ $(1 \leqq k \leqq s+1)$ で表す. $s$ 個より多く玉を取り出すと必ず赤玉が出るから, $s$ が偶数のとき \[\begin{aligned} P(A) &= p_1+p_3+\cdots +p_{s-1}+p_{s+1}, \\ P(B) &= p_2+p_4+\cdots +p_s \end{aligned}\] が, $s$ が奇数のとき \[\begin{aligned} P(A) &= p_1+p_3+\cdots +p_s, \\ P(B) &= p_2+p_4+\cdots +p_{s+1} \end{aligned}\] が成り立つ.
- (2)
- $p_k \geqq p_{k+1}$ が成り立つことを示す. $k$ 回目に勝者が決まらない確率を $q_k$ とおくと, \[\begin{aligned} p_{k+1} &= q_k\cdot\frac{r}{r+s-k} \quad \cdots [1], \\ q_{k+1} &= q_k\cdot\frac{s-k}{r+s-k} \end{aligned}\] となり, \[\begin{aligned} p_{k+2} &= q_{k+1}\cdot\frac{r}{r+s-k-1} \\ &= q_k\cdot\frac{s-k}{r+s-k}\cdot\frac{r}{r+s-k-1} \quad \cdots [2] \end{aligned}\] となる. $[1],$ $[2]$ の辺々を割ると \[\frac{p_{k+1}}{p_{k+2}} = \frac{r+s-k-1}{s-k}\] が得られる. 一方, $r \geqq 1$ から $r+s-k-1 \geqq s-k$ であるので, $\dfrac{p_{k+1}}{p_{k+2}} \geqq 1$ つまり $p_{k+1} \geqq p_{k+2}$ が成り立つ. また, \[ p_1 = \frac{r}{r+s}, \quad p_2 = \frac{s}{r+s}\cdot\frac{r}{r+s-1} = p_1\cdot\frac{s}{r+s-1}\] から $p_1 \geqq p_2$ であるので, $p_k \geqq p_{k+1}$ が成り立つ.
- (3)
- $P(A) = P(B)$ となる条件を求める. (1) のいずれの場合にも, $p_1 \geqq p_2,$ $p_3 \geqq p_4,$ $\cdots$ から, $P(A) \geqq P(B)$ が成り立つ. よって, $P(A)+P(B) = 1$ から \[ 2P(A) \geqq P(A)+P(B) = 1\] であるので, $P(A) \geqq \dfrac{1}{2}$ が成り立つ. $p_{s+1} \neq 0$ に注意すると, この等号が成り立つためには, $p_1 = p_2$ かつ $s$ が奇数であることが必要である. $p_1 = p_2$ のとき, $p_1 = p_1\cdot\dfrac{s}{r+s-1}$ から, $r = 1$ が成り立つ. 逆に, $r = 1$ かつ $s$ が奇数であるとき $P(A) = P(B)$ となるので, 求める条件は “$r = 1$ かつ $s$ は奇数” である.
クイズ《巴戦で優勝する確率》
A, B, C の $3$ 選手が巴戦で優勝決定戦を行う.
A, B の対戦から始めて, $2$ 試合目以降は直前の試合の勝者と控えの選手が対戦し, 先に $2$ 連勝した選手を優勝とする.
$3$ 選手の実力が互角であり, 各試合で引き分けはないとするとき, A, B, C が優勝する確率の比は何対何対何か.
(参考: $2016$ 東京大)
答え
$5:5:4.$
解説
$3$ 選手の実力は互角であるから, 試合の敗者が優勝する確率はどの時点でも等しい.
この確率を $p$ とおく.
A が優勝するのは “$1$ 試合目から $2$ 連勝する”, “$1$ 試合目で勝ち, $2$ 試合目で負けてその後優勝する”, “$1$ 試合目で負けてその後優勝する” のいずれかの場合であるから, その確率は
\[\frac{1}{2}\cdot\frac{1}{2}+\frac{1}{2}\cdot p+\frac{1}{2}\cdot\frac{1}{2}\cdot p = \frac{1}{4}+\frac{3}{4}p\]
である.
B が優勝する確率もこれに等しい.
C が優勝するのは “$2$ 試合目から $2$ 連勝する”, “$2$ 試合目に勝ち, $3$ 試合目で負けてその後優勝する” のいずれかの場合であるから,
\[\frac{1}{2}\cdot\frac{1}{2}+\frac{1}{2}\cdot\frac{1}{2}\cdot p = \frac{1}{4}+\frac{1}{4}p\]
である.
A, B, C が優勝する確率の和は $1$ であるから,
\[ 2\left(\frac{1}{4}+\frac{3}{4}p\right) +\left(\frac{1}{4}+\frac{1}{4}p\right) = 1\]
が成り立つ.
これを解くと,
\[ p = \frac{1}{7}\]
が得られる.
よって, A, B が優勝する確率はそれぞれ
\[\frac{1}{4}+\frac{3}{4}\cdot\frac{1}{7} = \frac{5}{14},\]
C が優勝する確率は
\[\frac{1}{4}+\frac{1}{4}\cdot\frac{1}{7} = \frac{2}{7}\]
である.
ゆえに, 求める確率の比は
\[\frac{5}{14}:\frac{5}{14}:\frac{2}{7} = 5:5:4\]
である.
クイズ《三角形の周上のランダム・ウォーク》
正三角形 $\mathrm{ABC}$ の頂点 $\mathrm A$ にいるアリが $1$ 秒ごとに異なる頂点に等確率で移動していくとき, $n$ 秒後に頂点 $\mathrm A$ にいる確率はいくらか.
(有名問題)
答え
$a_n = \dfrac{1}{3}+\dfrac{2}{3}\left( -\dfrac{1}{2}\right) ^n.$
解説
アリが $n$ 秒後に頂点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ にいる確率をそれぞれ $a_n,$ $b_n,$ $c_n$ とおく.
このとき,
\[\begin{aligned}
&a_{n+1} = \frac{1}{2}b_n+\frac{1}{2}c_n, \\
&a_n+b_n+c_n = 1
\end{aligned}\]
であるから,
$a_{n+1} = \dfrac{1}{2}(1-a_n)$ つまり $a_{n+1} = -\dfrac{1}{2}a_n+\dfrac{1}{2}$
が成り立つ.
両辺から $\alpha = -\dfrac{1}{2}\alpha +\dfrac{1}{2}$ の解 $\alpha = \dfrac{1}{3}$ を引いて整理すると,
\[ a_{n+1}-\frac{1}{3} = -\frac{1}{2}\left( a_n-\frac{1}{3}\right)\]
が得られる.
よって, $\left\{ a_n-\dfrac{1}{3}\right\}$ は第 $0$ 項 $a_0-\dfrac{1}{3} = 1-\dfrac{1}{3} = \dfrac{2}{3},$ 公比 $-\dfrac{1}{2}$ の等比数列であるから,
$a_n-\dfrac{1}{3} = \dfrac{2}{3}\left( -\dfrac{1}{2}\right) ^n$ つまり $a_n = \dfrac{1}{3}+\dfrac{2}{3}\left( -\dfrac{1}{2}\right) ^n$
である.
クイズ《紅白まんじゅうの交換》
A, B がそれぞれ紅白のまんじゅうが $1$ 個ずつ入った袋を持っている.
A, B が各自の袋からまんじゅうを $1$ 個取り出して交換して袋にしまうという操作を $n$ 回繰り返したとき, A, B がともに紅白のまんじゅうを $1$ 個ずつ持っている確率はいくらか.
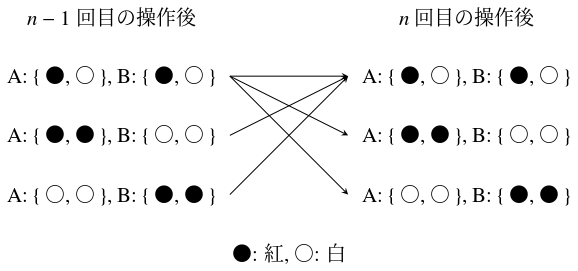

(有名問題, 参考: 兵庫県立大)
答え
$\dfrac{2}{3}+\dfrac{1}{3}\left( -\dfrac{1}{2}\right)^n.$
解説
まんじゅうを交換する操作を $n$ 回 $(n \geqq 0)$ 行った後に, A が紅色 $1$ 個, 白色 $1$ 個を持っている確率を $m_n$ (m: mixed-color), 紅色 $2$ 個を持っている確率を $r_n$ (r: red), 白色 $2$ 個を持っている確率を $w_n$ (w: white) とおく.
このとき,
\[ m_0 = 1, \quad r_0 = w_0 = 0\]
であり,
A, B がともに紅色 $1$ 個, 白色 $1$ 個を持っている状態からは,
\[\frac{1}{2}\cdot\frac{1}{2}+\frac{1}{2}\cdot\frac{1}{2} = \frac{1}{2}\]
の確率で同じ状態になり,
\[\frac{1}{2}\cdot\frac{1}{2} = \frac{1}{4}\]
の確率で A が紅色 $2$ 個, B が白色 $2$ 個の状態になり, これと同じ確率で A が白色 $2$ 個, B が紅色 $2$ 個の状態になる.
また, A が紅色 $2$ 個, B が白色 $2$ 個の状態, および A が白色 $2$ 個, B が紅色 $2$ 個の状態からは, 必ず A, B がともに紅色 $1$ 個, 白色 $1$ 個を持っている状態になる (下図).
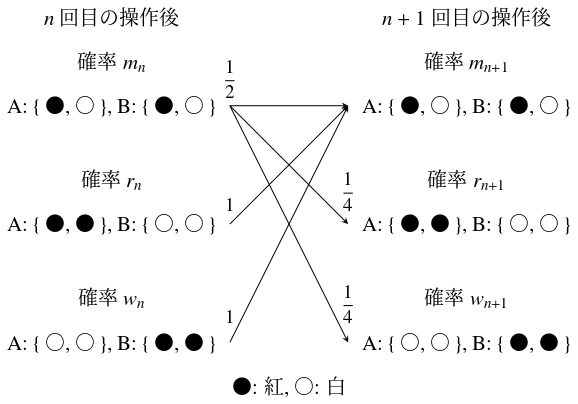 よって,
\[\begin{aligned}
&m_{n+1} = \frac{1}{2}m_n+r_n+w_n \quad \cdots [1], \\
&r_{n+1} = w_{n+1} = \frac{1}{4}m_n \quad \cdots [2]
\end{aligned}\]
が成り立つ.
また,
\[ m_n+r_n+w_n = 1\]
であるので, $[1]$ から $r_n,$ $w_n$ を消去すると
\[ m_{n+1} = \frac{1}{2}m_n+(1-m_n)\]
つまり
\[ m_{n+1} = 1-\frac{1}{2}m_n \quad \cdots [3]\]
が得られる.
$[3]$ の辺々から
\[\alpha = 1-\frac{1}{2}\alpha\]
の解 $\alpha = \dfrac{2}{3}$ を引くと
\[ m_{n+1}-\frac{2}{3} = -\frac{1}{2}\left( m_n-\frac{2}{3}\right)\]
となるから, 数列 $\left\{ m_n-\dfrac{2}{3}\right\}$ は第 $0$ 項 $m_0-\dfrac{2}{3} = \dfrac{1}{3},$ 公比 $-\dfrac{1}{2}$ の等比数列である.
ゆえに,
\[ m_n-\frac{2}{3} = \frac{1}{3}\left( -\frac{1}{2}\right) ^n\]
つまり
\[ m_n = \frac{2}{3}+\frac{1}{3}\left( -\frac{1}{2}\right) ^n \quad \cdots [4]\]
である.
ちなみに, $[2]$ から $r_n = w_n = \dfrac{1}{4}m_{n-1}$ $(n \geqq 1)$ であるので, $[4]$ により
\[ r_n = w_n = \frac{1}{6}+\frac{1}{12}\left( -\frac{1}{2}\right) ^{n-1} = \frac{1}{6}-\frac{1}{6}\left( -\frac{1}{2}\right) ^n\]
である (これは $n = 0$ のときも成り立つ).
よって,
\[\begin{aligned}
&m_{n+1} = \frac{1}{2}m_n+r_n+w_n \quad \cdots [1], \\
&r_{n+1} = w_{n+1} = \frac{1}{4}m_n \quad \cdots [2]
\end{aligned}\]
が成り立つ.
また,
\[ m_n+r_n+w_n = 1\]
であるので, $[1]$ から $r_n,$ $w_n$ を消去すると
\[ m_{n+1} = \frac{1}{2}m_n+(1-m_n)\]
つまり
\[ m_{n+1} = 1-\frac{1}{2}m_n \quad \cdots [3]\]
が得られる.
$[3]$ の辺々から
\[\alpha = 1-\frac{1}{2}\alpha\]
の解 $\alpha = \dfrac{2}{3}$ を引くと
\[ m_{n+1}-\frac{2}{3} = -\frac{1}{2}\left( m_n-\frac{2}{3}\right)\]
となるから, 数列 $\left\{ m_n-\dfrac{2}{3}\right\}$ は第 $0$ 項 $m_0-\dfrac{2}{3} = \dfrac{1}{3},$ 公比 $-\dfrac{1}{2}$ の等比数列である.
ゆえに,
\[ m_n-\frac{2}{3} = \frac{1}{3}\left( -\frac{1}{2}\right) ^n\]
つまり
\[ m_n = \frac{2}{3}+\frac{1}{3}\left( -\frac{1}{2}\right) ^n \quad \cdots [4]\]
である.
ちなみに, $[2]$ から $r_n = w_n = \dfrac{1}{4}m_{n-1}$ $(n \geqq 1)$ であるので, $[4]$ により
\[ r_n = w_n = \frac{1}{6}+\frac{1}{12}\left( -\frac{1}{2}\right) ^{n-1} = \frac{1}{6}-\frac{1}{6}\left( -\frac{1}{2}\right) ^n\]
である (これは $n = 0$ のときも成り立つ).

クイズ《テニスの勝率》
A, B がテニスの試合している.
A のサービス・ゲームにおいて, A のポイント獲得率が B のポイント獲得率の $2$ 倍であるとき, デュースになった時点から A がこのゲームをとる確率はいくらか.
※ $3$ ポイント以上とって差を $2$ ポイント以上つけた方がゲームをとり, 両者 $3$ ポイント以上の引き分けをデュースと呼ぶ.
※ $3$ ポイント以上とって差を $2$ ポイント以上つけた方がゲームをとり, 両者 $3$ ポイント以上の引き分けをデュースと呼ぶ.
(参考: G・ブロム, L・ホルスト, D・サンデル『確率論へようこそ』)
答え
$\dfrac{4}{5}.$
解説
A のポイント獲得率を $a,$ B のポイント獲得率を $b$ とおく.
\[ a+b = 1, \quad a = 2b\]
から,
\[ a = \frac{2}{3}, \quad b = \frac{1}{3}\]
である.
簡単のため, このゲーム内のポイントを $0$ - $15$ のようには数えず, $0$ - $1$ のように数える ($3$ - $3$ 以上の引き分けがデュース).
ポイントが $i$ - $j$ になった時点から A がゲームをとる確率を $P(i,j)$ で表す.
求める確率は $P(3,3)$ である.
このとき,
\[ P(i,j) = aP(i+1,j)+bP(i,j+1)\]
が成り立ち, 特に
\[\begin{aligned}
P(3,3) &= aP(4,3)+b(3,4) \quad \cdots [1], \\
P(4,3) &= aP(5,3)+b(4,4) \quad \cdots [2], \\
P(3,4) &= aP(4,4)+b(3,5) \quad \cdots [3]
\end{aligned}\]
である.
$[2],$ $[3]$ を $[1]$ に代入して整理すると,
\[ P(3,3) = a^2P(5,3)+2abP(4,4)+b^2P(3,5)\]
が得られる.
ここで
\[ P(5,3) = 1, \quad P(4,4) = P(3,3), \quad P(3,5) = 0\]
であるから, 求める確率は
\[\begin{aligned}
P(3,3) &= \frac{a^2}{1-2ab} \\
&= \frac{\left(\dfrac{2}{3}\right) ^2}{1-2\cdot\dfrac{2}{3}\cdot\dfrac{1}{3}} = \frac{4}{5}
\end{aligned}\]
である.
参考
上記の漸化式により, $a = nb$ ($n$: 整数) のとき, A がこのゲームをとる確率は
\[ P(0,0) = \frac{n^7+5n^6+11n^5+15n^4}{n^7+5n^6+11n^5+15n^4+15n^3+11n^2+5n+1}\]
であることが示せる (ヤコブ・ベルヌーイ, $1713$ 年).
期待値
クイズ《じゃんけんの勝者の人数》
$1$ 回だけじゃんけんをするとき, 勝者の人数が最も多くなると見込まれるのは, 何人でじゃんけんをするときか.
(オリジナル)
答え
$4$ 人.
解説
$n$ を $2$ 以上の整数とする.
$n$ 人で $1$ 回だけじゃんけんをするとき, 勝者の人数を $X_n$ とおく.
求めるべきは, $X_n$ の期待値 $E(X_n)$ を最大にする $n$ の値である.
- (1)
- まず, 勝者が $k$ 人 $(1 \leqq k \leqq n-1)$ である確率 $P(X_n = k)$ を求める. $n$ 人のじゃんけんで, 全員の手の出し方は $3^n$ 通りある. 勝者が $k$ 人 $(1 \leqq k \leqq n-1)$ であるとき, 勝者と敗者を分ける方法が ${}_n\mathrm C_k$ 通りあり, そのおのおのに対して勝者と敗者の手の組合せが ${}_3\mathrm C_2$ 通りあるから, $X_n = k$ となる確率は \[ P(X_n = k) = \frac{{}_n\mathrm C_k\cdot {}_3\mathrm C_2}{3^n} = \frac{{}_n\mathrm C_k}{3^{n-1}} \quad \cdots [1]\] である.
- (2)
- 次に, $X_n$ の期待値 $E(X_n)$ を求める. $X_n$ は $0$ 以上 $n-1$ 以下の整数の値をとるから, $[1]$ により, $X_n$ の期待値は \[\begin{aligned} E(X_n) &= \sum_{k = 0}^{n-1}kP(X_n = k) \\ &= \sum_{k = 1}^{n-1}kP(X_n = k) \quad (\because 0\cdot P(X_n = 0) = 0) \\ &= \sum_{k = 1}^{n-1}k\cdot\frac{{}_n\mathrm C_k}{3^{n-1}} \quad (\because [1]) \\ &= \sum_{k = 1}^{n-1}n\cdot\frac{{}_{n-1}\mathrm C_{k-1}}{3^{n-1}} \quad (\because k\,{}_n\mathrm C_k = n\,{}_{n-1}\mathrm C_{k-1}) \\ &= \frac{n}{3^{n-1}}\sum_{k = 1}^{n-1}{}_{n-1}\mathrm C_{k-1} \\ &= \frac{n}{3^{n-1}}\{ (1+1)^{n-1}-{}_{n-1}\mathrm C_{n-1}\} \\ &= \frac{n(2^{n-1}-1)}{3^{n-1}} \end{aligned}\] である. 最後から $2$ つめの等号では二項定理を使った.
- (3)
- 最後に, $E(X_n)$ を最大にする $n$ の値を求める. \[\begin{aligned} \frac{E(X_{n+1})}{E(X_n)} &= \frac{(n+1)(2^n-1)}{3^n}\cdot\frac{3^{n-1}}{n(2^{n-1}-1)} \\ &= \frac{(2n+2)(2^n-1)}{3n(2^n-2)} \end{aligned}\] であるから, $n \geqq 3$ のとき \[\begin{aligned} &E(X_n) > E(X_{n+1}) \iff \frac{E(X_{n+1})}{E(X_n)} < 1 \\ &\iff \frac{(2n+2)(2^n-1)}{3n(2^n-2)} < 1 \\ &\iff (2n+2)(2^n-1) < 3n(2^n-2) \\ &\iff 4n-2 < (n-2)2^n \\ &\iff \frac{4n-2}{n-2} < 2^n \iff 4+\frac{6}{n-2} < 2^n \\ &\iff n \geqq 4 \quad \left(\because 4+\frac{6}{n-2} \leqq 10\right) \end{aligned}\] が成り立つ. また, \[ E(X_2) = \frac{2}{3}, \quad E(X_3) = 1, \quad E(X_4) = \frac{28}{27}\] である. よって, \[ E(X_2) < E(X_3) < E(X_4) > E(X_5) > E(X_6) > \cdots\] であるから, $E(X_n)$ は $n = 4$ のとき最大値 $\dfrac{28}{27}$ をとる.
参考
- $n$ が小さいときの $E(X_n)$ の近似値は, 次の表の通りである.
$n$ $2$ $3$ $4$ $5$ $E(X_n)$ $0.666\cdots$ $1$ $1.037\cdots$ $0.925\cdots$ $6$ $7$ $8$ $9$ $10$ $0.765\cdots$ $0.604\cdots$ $0.464\cdots$ $0.349\cdots$ $0.259\cdots$ - 極限値 $\lim\limits_{n \to \infty}E(X_n)$ については, こちらを参照されたい.
クイズ《赤玉が出るまでに取り出す玉の個数》
$r$ 個の赤玉を含む $n$ 個の玉を袋に入れる.
- (1)
- 赤玉が出るまで $1$ 個ずつ玉を取り出すとき, 何個目に赤玉を取り出すと見込まれるか.
- (2)
- すべての赤玉が出るまで $1$ 個ずつ玉を取り出すとき, 何個目に最後の赤玉を取り出すと見込まれるか.
(有名問題)
答え
- (1)
- $\dfrac{r+1}{n+1}$ 個目.
- (2)
- $\dfrac{r(n+1)}{r+1}$ 個目.
解説
すべての玉を区別して考える.
- (1)
- 最小で $1$ 個, 最大で $n-r+1$ 個玉を取り出せば, 赤玉が出る. $k$ 個目 $(1 \leqq k \leqq n-r+1)$ に赤玉を取り出すとき, $n-k$ 個中 $r-1$ 個の赤玉が残るから, 残った玉の組合せは ${}_{n-k}\mathrm C_{r-1}$ 通りある. これは $k$ 個目に赤玉を取り出す方法の総数に等しいから, その確率は \[\frac{{}_{n-k}\mathrm C_{r-1}}{{}_n\mathrm C_r}\] である. ゆえに, 赤玉が出るまでに取り出す玉の個数の期待値は, \[\begin{aligned} &1\cdot\frac{{}_{n-1}\mathrm C_{r-1}}{{}_n\mathrm C_r}+\cdots +k\cdot\frac{{}_{n-k}\mathrm C_{r-1}}{{}_n\mathrm C_r}+\cdots +(n-r+1)\cdot\frac{{}_{r-1}\mathrm C_{r-1}}{{}_n\mathrm C_r} \\ &= \frac{1}{{}_n\mathrm C_r}\left(\begin{array}{ccccc} {}_{n-1}\mathrm C_{r-1}+ & \cdots & +{}_{n-k}\mathrm C_{r-1}+ & \cdots & +{}_{r-1}\mathrm C_{r-1} \\ {} & \ddots & \vdots & {} & \vdots \\ {} & {} & +{}_{n-k}\mathrm C_{r-1}+ & \cdots & +{}_{r-1}\mathrm C_{r-1} \\ {} & {} & {} & \ddots & \vdots \\ {} & {} & {} & {} & +{}_{r-1}\mathrm C_{r-1} \end{array}\right) \\ &= \frac{1}{{}_n\mathrm C_r}({}_n\mathrm C_r+\cdots +{}_{n-k+1}\mathrm C_r+\cdots +{}_r\mathrm C_r) \\ &= \frac{1}{{}_n\mathrm C_r}\cdot{}_{n+1}\mathrm C_{r+1} \\ &= \frac{(n+1)!}{(r+1)!(n-r)!}\div\frac{n!}{r!(n-r)!} \\ &= \frac{n+1}{r+1} \end{aligned}\] である. ここで, 第 $2,$ 第 $3$ の等号では「ホッケー・スティック恒等式」 \[ {}_n\mathrm C_r+\cdots +{}_r\mathrm C_r = {}_{n+1}\mathrm C_{r+1} \quad (0 \leqq r < n)\] (こちらを参照) を使った.
- (2)
- 最小で $r$ 個, 最大で $n$ 個玉を取り出せば, すべての赤玉が出る. $k$ 個目 $(r \leqq k \leqq n)$ に最後の赤玉を取り出すとき, $k-1$ 個目までに $r-1$ 個の赤玉を取り出す. その方法は ${}_{k-1}\mathrm C_{r-1}$ 通りあるから, その確率は \[\frac{{}_{k-1}\mathrm C_{r-1}}{{}_n\mathrm C_r}\] である. ゆえに, すべての赤玉が出るまでに取り出す玉の個数の期待値は, \[\begin{aligned} \sum_{k = r}^nk\cdot\frac{{}_{k-1}\mathrm C_{r-1}}{{}_n\mathrm C_r} &= \frac{1}{{}_n\mathrm C_r}\sum_{k = r}^nr\cdot{}_k\mathrm C_r \quad (\because k\cdot{}_{k-1}\mathrm C_{r-1} = r\cdot{}_k\mathrm C_r) \\ &= \frac{r\cdot{}_{n+1}\mathrm C_{r+1}}{{}_n\mathrm C_r} \\ &= \frac{r\cdot\dfrac{n+1}{r+1}{}_n\mathrm C_r}{{}_n\mathrm C_r} \quad (\because{}_{n+1}\mathrm C_{r+1} = \frac{n+1}{r+1}\cdot{}_n\mathrm C_r) \\ &= \frac{r(n+1)}{r+1} \end{aligned}\] である. ここで, 第 $2$ の等号では「ホッケー・スティック恒等式」 \[\sum_{k = r}^n{}_k\mathrm C_r = {}_{n+1}\mathrm C_{r+1} \quad (0 \leqq r < n)\] (こちらを参照) を使った.
クイズ《仕切り板の間にある本の冊数》
$n$ 冊の本と $r$ 枚の仕切り板がある.
これらを無作為に $1$ 列に並べて空の本棚に収納するとき, 隣り合う $2$ 枚の仕切り板の間にある本は平均的に何冊になると見込まれるか.
(オリジナル)
答え
$\dfrac{n}{r+1}$ 冊.
解説
本棚の左端を左から $0$ 枚目の仕切り板, 本棚の右端を左から $r+1$ 枚目の仕切り板とみなし, 各整数 $i$ $(0 \leqq i \leqq r)$ に対して, 左から $i$ 枚目と $i+1$ 枚目の仕切り板の間にある本の冊数を $X_i$ とおく.
求める値は $X_i$ の期待値 $E(X_i)$ である.
$n$ 冊の本を同じものとみなし, $r$ 枚の仕切り板を同じものとみなすとき, 仕切り板の入れ方は ${}_{n+r}\mathrm C_r$ 通り.
このうち, $X_i = k$ $(0 \leqq k \leqq n)$ となる場合の数は `` 仕切り板 $2$ 枚と本 $k$ 冊 '' を仕切り板 $1$ 枚とみなして仕切り板を入れる場合の数に等しく ${}_{n+r-k-1}\mathrm C_{r-1}$ 通りあるから, $X_i = k$ となる確率は \[ P(X_i = k) = \frac{{}_{n+r-k-1}\mathrm C_{r-1}}{{}_{n+r}\mathrm C_r}\] である.
ゆえに, 求める期待値は, \[\begin{aligned} E(X_i) &= \sum_{k = 0}^nkP(X_i = k) \\ &= \frac{1}{{}_{n+r}\mathrm C_r}\sum_{k = 0}^n k\cdot{}_{n+r-k-1}\mathrm C_{r-1} \\ &= \frac{1}{{}_{n+r}\mathrm C_r}\sum_{k = 1}^n k\cdot{}_{n+r-k-1}\mathrm C_{r-1} \\ &= \frac{1}{{}_{n+r}\mathrm C_r}\left(\begin{array}{rrrr} {}_{n+r-2}\mathrm C_{r-1} & {} & {} & {} \\ +{}_{n+r-3}\mathrm C_{r-1} & \!\!\!\!+{}_{n+r-3}\mathrm C_{r-1} & {} & {} \\ \vdots\,\;\quad & \vdots\,\;\quad & \ddots & {} \\ +{}_{r-1}\mathrm C_{r-1} & \!\!\!\!+{}_{r-1}\mathrm C_{r-1} & \!\!\!\!+\cdots & \!\!\!\!+{}_{r-1}\mathrm C_{r-1} \end{array}\right) \\ &= \frac{1}{{}_{n+r}\mathrm C_r}\left({}_{n+r-1}\mathrm C_r+{}_{n+r-2}\mathrm C_r+\cdots +{}_r\mathrm C_r\right) \\ &= \frac{1}{{}_{n+r}\mathrm C_r}\cdot{}_{n+r}\mathrm C_{r+1} \\ &= \frac{n!r!}{(n+r)!}\cdot\frac{(n+r)!}{(n-1)!(r+1)!} \\ &= \frac{n}{r+1} \end{aligned}\] である. ここで, 第 $5,$ 第 $6$ の等号では「ホッケー・スティック恒等式」 \[\sum_{k = r}^n{}_k\mathrm C_r = {}_{n+1}\mathrm C_{r+1} \quad (0 \leqq r < n)\] (こちらを参照) を使った.
$n$ 冊の本を同じものとみなし, $r$ 枚の仕切り板を同じものとみなすとき, 仕切り板の入れ方は ${}_{n+r}\mathrm C_r$ 通り.
このうち, $X_i = k$ $(0 \leqq k \leqq n)$ となる場合の数は `` 仕切り板 $2$ 枚と本 $k$ 冊 '' を仕切り板 $1$ 枚とみなして仕切り板を入れる場合の数に等しく ${}_{n+r-k-1}\mathrm C_{r-1}$ 通りあるから, $X_i = k$ となる確率は \[ P(X_i = k) = \frac{{}_{n+r-k-1}\mathrm C_{r-1}}{{}_{n+r}\mathrm C_r}\] である.
ゆえに, 求める期待値は, \[\begin{aligned} E(X_i) &= \sum_{k = 0}^nkP(X_i = k) \\ &= \frac{1}{{}_{n+r}\mathrm C_r}\sum_{k = 0}^n k\cdot{}_{n+r-k-1}\mathrm C_{r-1} \\ &= \frac{1}{{}_{n+r}\mathrm C_r}\sum_{k = 1}^n k\cdot{}_{n+r-k-1}\mathrm C_{r-1} \\ &= \frac{1}{{}_{n+r}\mathrm C_r}\left(\begin{array}{rrrr} {}_{n+r-2}\mathrm C_{r-1} & {} & {} & {} \\ +{}_{n+r-3}\mathrm C_{r-1} & \!\!\!\!+{}_{n+r-3}\mathrm C_{r-1} & {} & {} \\ \vdots\,\;\quad & \vdots\,\;\quad & \ddots & {} \\ +{}_{r-1}\mathrm C_{r-1} & \!\!\!\!+{}_{r-1}\mathrm C_{r-1} & \!\!\!\!+\cdots & \!\!\!\!+{}_{r-1}\mathrm C_{r-1} \end{array}\right) \\ &= \frac{1}{{}_{n+r}\mathrm C_r}\left({}_{n+r-1}\mathrm C_r+{}_{n+r-2}\mathrm C_r+\cdots +{}_r\mathrm C_r\right) \\ &= \frac{1}{{}_{n+r}\mathrm C_r}\cdot{}_{n+r}\mathrm C_{r+1} \\ &= \frac{n!r!}{(n+r)!}\cdot\frac{(n+r)!}{(n-1)!(r+1)!} \\ &= \frac{n}{r+1} \end{aligned}\] である. ここで, 第 $5,$ 第 $6$ の等号では「ホッケー・スティック恒等式」 \[\sum_{k = r}^n{}_k\mathrm C_r = {}_{n+1}\mathrm C_{r+1} \quad (0 \leqq r < n)\] (こちらを参照) を使った.
クイズ《夫婦円卓問題》
$n$ 組 $(n \geqq 2)$ の夫婦 $2n$ 人が, 男女交互に, それ以外は無作為に円卓の周りに座るとき, 隣どうしに座ると見込まれる夫婦は何組か.
(有名問題)
答え
$2$ 組.
解説
隣どうしに座る夫婦の総数を $X$ とおく.
求めるべきは, $X$ の期待値 $E(X)$ である.
席に $1$ から $2n$ までの番号をつけて, 各番号 $k$ $(1 \leqq k \leqq 2n)$ に対して, 番号 $k$ の席に座る人とその右隣に座る人が夫婦であるとき $X_k = 1,$ そうでないとき $X_k = 0$ と定める. $n \geqq 2$ に注意すると, 隣どうしに座る夫婦の総数 $X$ は右隣に伴侶が座る人の総数に等しいから, \[ X = X_1+\cdots +X_{2n} \quad \cdots [1]\] が成り立つ.
席に $1$ から $2n$ までの番号をつけて, 各番号 $k$ $(1 \leqq k \leqq 2n)$ に対して, 番号 $k$ の席に座る人とその右隣に座る人が夫婦であるとき $X_k = 1,$ そうでないとき $X_k = 0$ と定める. $n \geqq 2$ に注意すると, 隣どうしに座る夫婦の総数 $X$ は右隣に伴侶が座る人の総数に等しいから, \[ X = X_1+\cdots +X_{2n} \quad \cdots [1]\] が成り立つ.
- (1)
- まず, $X_k$ の期待値 $E(X_k)$ $(1 \leqq k \leqq 2n)$ を求める. 番号 $k$ の席に座る人とその右隣に座る人が夫婦である確率は $\dfrac{1}{n},$ そうでない確率は $\dfrac{n-1}{n}$ であるから, \[ E(X_k) = 0\cdot\frac{n-1}{n}+1\cdot\frac{1}{n} = \frac{1}{n} \quad \cdots [2]\] である.
- (2)
- 次に, $X$ の期待値 $E(X)$ を求める. $[1],$ $[2]$ により, \[\begin{aligned} E(X) &= E(X_1+\cdots +X_{2n}) = E(X_1)+\cdots +E(X_{2n}) \\ &= 2n\cdot\frac{1}{n} = 2 \end{aligned}\] である.
クイズ《さいころですべての目を出すまでにかかる回数》
$n$ 面のさいころがある.
すべての目を出すには, 平均的に何回さいころをふればよいと見込まれるか (ヒント: 正の整数全体を値域とする確率変数 $W$ の期待値は
\[ E(W) = \sum_{m = 1}^\infty m\,P(W = m)\]
で定義される).
(有名問題)
答え
$n\displaystyle\sum_{k = 1}^n\frac{1}{k}$ 回.
解説
-
事象 $A_1,$ $\cdots,$ $A_n$ のいずれかが等確率で起こる試行の反復試行において, $A_1,$ $\cdots,$ $A_n$ がすべて $1$ 回以上起こるまでに要する試行回数 $X$ の期待値 $E(X)$ を求めればよい.
$A_1,$ $\cdots,$ $A_n$ のうち $k$ 個 $(0 \leqq k \leqq n-1)$ が起こった状態から別の事象が起こるまでに要する試行回数を $X_k$ とおくと,
\[ X = \sum_{k = 0}^{n-1}X_k\]
となる.
期待値の線形性により
\[ E(X) = \sum_{k = 0}^{n-1}E(X_k) = \sum_{k = 0}^{n-1}\frac{n}{n-k} = n\sum_{k = 1}^n\frac{1}{k}\]
であるから, $E(X_k)$ の値を求める.
$X_k = m$ ($m$: 正の整数) となるのは, $m-1$ 回はすでに起こった $k$ 個の事象以外は起こらず, その次に残り $n-k$ 個のうち $1$ つの事象が起こる場合であるから,
\[ P(X_k = m) = \left(\dfrac{k}{n}\right) ^{m-1}\dfrac{n-k}{n}\]
である.
よって,
\[\begin{aligned}
E(X_k) &= \sum_{m = 1}^\infty m\,P(X_k = m) = \sum_{m = 1}^\infty m\left(\frac{k}{n}\right) ^{m-1}\frac{n-k}{n} \\
&= \frac{n-k}{n}\left( 1-\dfrac{k}{n}\right) ^{-2} = \frac{n-k}{n}\left(\dfrac{n-k}{n}\right) ^{-2} \\
&= \frac{n}{n-k}
\end{aligned}\]
である.
ここで第 $3$ の等号では, $r = \dfrac{k}{n}$ に対して
\[\sum_{m = 1}^\infty mr^{m-1} = \frac{1}{(1-r)^2}\]
が成り立つことを使った ($r = 0$ のときは自明, $0 < r < 1$ のときの証明はこちらを参照).
ゆえに, 求める期待値は
\[ E(X) = \sum_{k = 0}^{n-1}\frac{n}{n-k} = n\sum_{k = 1}^n\dfrac{1}{k}\]
である.
参考
- $n$ 種類のアイテムのうち $1$ 種類がランダムに封入されたカプセル・トイで全種類のアイテムを集めるにも, 平均的にこの回数繰り返せばよいと見込まれる.
- この種の問題はしばしば「クーポン・コレクターの問題」(coupon collector's problem) または「食玩問題」と呼ばれる.
- 無限級数 $\displaystyle\lim_{n \to \infty}\left(\sum_{k = 1}^n\frac{1}{k}-\log n\right)$ は収束し, その和 $\gamma = 0.57721\cdots$ を「オイラーの定数」(Euler's constant) と呼ぶ. \[\lim_{n \to \infty}n\sum_{k = 1}^n\frac{1}{k}\!-\!\lim_{n \to \infty}n(\log n\!+\!\gamma ) \!=\! \lim_{n \to \infty}\left(\sum_{k = 1}^n\frac{1}{k}\!-\!\log n\!-\!\gamma\right) \!=\! 0\] であるから, $n$ が十分に大きいとき, $E(X)$ は近似的に $n(\log n+\gamma )$ に等しいと言える.
- $n$ が小さいときの $E(X)$ の値は, 次の表の通りである.
$n$ $1$ $2$ $3$ $4$ $E(X)$ $1$ $3$ $\dfrac{11}{2}$
$= 5.5$$\dfrac{25}{3}$
$= 8.33\cdots$$n$ $5$ $6$ $7$ $8$ $E(X)$ $\dfrac{137}{12}$
$= 11.41\cdots$$\dfrac{147}{10}$
$= 14.7$$\dfrac{363}{20}$
$= 18.15$$\dfrac{761}{35}$
$= 21.74\cdots$$n$ $9$ $10$ $11$ $12$ $E(X)$ $\dfrac{7129}{280}$
$= 25.46\cdots$$\dfrac{7381}{252}$
$= 29.28\cdots$$\dfrac{83711}{2520}$
$= 33.21\cdots$$\dfrac{86021}{2310}$
$= 37.23\cdots$