最小シュタイナー木問題
分岐点を新たに設けてもよいという条件の下で, 与えられたいくつかの点をもれなく結ぶ最短経路を求める問題は,
最小シュタイナー木問題 (the shortest path problem) と呼ばれ,
インフラの建設計画を立てたり, 電気回路の設計をしたりする際に現れる素朴で重要な問題である.
$3$ 点の場合
定理《内積の不等式と三角形のフェルマー点》
$3$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ を結ぶ最短経路は,
- (i)
- $3$ 点が一直線上にあるとき, 最も離れた $2$ 点を結ぶ線分である.
- (ii)
- $3$ 点がどの内角も $120^\circ$ 未満であるような三角形をなすとき, $\angle\mathrm{AFB} = \angle\mathrm{BFC} = \angle\mathrm{CFA}$ なる点 $\mathrm F$ を交差点として $3$ 点を結ぶ三叉路である. 点 $\mathrm F$ は, $\triangle\mathrm{ABC}$ と $1$ 辺を共有する正三角形 $\mathrm{ABC}',$ $\mathrm{BCA}',$ $\mathrm{CAB}'$ を $\triangle\mathrm{ABC}$ の外側に描くとき, $3$ 直線 $\mathrm{AA}',$ $\mathrm{BB}',$ $\mathrm{CC}'$ の交点として定まる.
- (iii)
- $3$ 点がある内角が $120^\circ$ 以上であるような三角形をなすとき, その頂点と他の $2$ 頂点を結ぶ折れ線である.
証明
- (i)
- 明らか.
- (ii)
- 前半: 三角不等式 $\mathrm P_1\mathrm P_2+\mathrm P_2\mathrm P_3 \geqq \mathrm P_1\mathrm P_3$ を使うと, これは三角形の各頂点までの距離の和が最小になる点を求める問題に帰着できる (詳細は割愛する).
その最小値を求める問題については, こちらを参照.
後半: $2$ 直線 $\mathrm{AA}',$ $\mathrm{BB}'$ の交点を $\mathrm F$ とおき, $\angle\mathrm{AFB} = \angle\mathrm{BFC} = \angle\mathrm{CFA}$ を示す. $\mathrm{CA} = \mathrm{CB}',$ $\mathrm{CB} = \mathrm{CA}',$ $\angle\mathrm{ACA'} = \angle\mathrm{BCB'} = \angle\mathrm{ACB}+60^\circ$ から $\triangle\mathrm{ACA}' \equiv \triangle\mathrm B'\mathrm{CB}$ であるので, $\angle\mathrm{CAF} = \angle\mathrm{CB}'\mathrm F,$ $\angle\mathrm{CBF} = \angle\mathrm{CA}'\mathrm F$ となる. よって, 円周角の定理の逆により, $4$ 点 $\mathrm C,$ $\mathrm F,$ $\mathrm A,$ $\mathrm B'$ と $4$ 点 $\mathrm C,$ $\mathrm F,$ $\mathrm B,$ $\mathrm A'$ はそれぞれ同一円周上にあるので, $\angle\mathrm{BFC} = \angle\mathrm{CFA} = 180^\circ -60^\circ = 120^\circ$ となり, $\angle\mathrm{AFB} = 360^\circ -\angle\mathrm{BFC}-\angle\mathrm{CFA} = 120^\circ$ となる.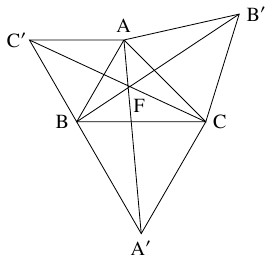
- (iii)
- 平面上に点 $\mathrm P$ をとる.
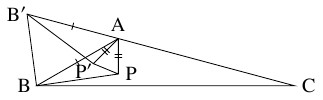
$\mathrm P \neq \mathrm A$ のとき, 半直線 $\mathrm{CA}$ 上に $\mathrm{AB} = \mathrm{AB}'$ となるように点 $\mathrm B'$ をとり, $\triangle\mathrm{APB} \equiv \triangle\mathrm{AP}'\mathrm B'$ となるように点 $\mathrm P'$ をとると, 仮定から $\triangle\mathrm{APP}'$ は頂角が $60^\circ$ 以下の二等辺三角形となるので, $\mathrm{PA} \geqq \mathrm{PP}'$ となり,
\[\begin{aligned}
\mathrm{PA}+\mathrm{PB}+\mathrm{PC} &\geqq \mathrm B'\mathrm P'+\mathrm P'\mathrm P+\mathrm{PC} \\
&> \mathrm B'\mathrm C = \mathrm B'\mathrm A+\mathrm{AC} = \mathrm{BA}+\mathrm{AC}
\end{aligned}\]
となる.
よって, $\mathrm{AP}+\mathrm{BP}+\mathrm{CP}$ は $\mathrm P = \mathrm A$ のとき最小になる.
定義《フェルマー点》
$\triangle\mathrm{ABC}$ の各頂点までの距離の和が最小となるような点を $\triangle\mathrm{ABC}$ のフェルマー点またはトリチェリ点 (Fermat point, Torricelli point) と呼ぶ.
正方形の $4$ 頂点の場合
定理《正方形の $4$ 頂点の最小シュタイナー木問題》
正方形 $\mathrm{ABCD}$ の $4$ 頂点を結ぶ最短経路は,
\[\mathrm{PA} = \mathrm{QB} = \mathrm{QC} = \mathrm{PD},\ \angle\mathrm{APD} = \angle\mathrm{BQC} = 120^\circ\]
を満たす正方形の内部の点 $\mathrm P,$ $\mathrm Q$ について,
$2$ 本折れ線 $\mathrm{APD},$ $\mathrm{BQC}$ を線分 $\mathrm{PQ}$ でつないだ経路である.
証明
三角不等式を使った議論により, 分岐点が $2$ 個の場合に帰着できる (詳細は省略).
対称性に着目すると, その $2$ 点が線分 $\mathrm{AD}$ の垂直二等分線上にある場合に帰着できる.
その先の証明については, こちらを参照.
高校数学の問題
ベクトル
問題《内積の不等式と三角形のフェルマー点》
- (1)
- 平面上の単位ベクトル $\overrightarrow{e_1},$ $\overrightarrow{e_2},$ $\overrightarrow{e_3}$ が $\overrightarrow{e_1}+\overrightarrow{e_2}+\overrightarrow{e_3} = \vec 0$ を満たすとする. $\overrightarrow{e_1},$ $\overrightarrow{e_2},$ $\overrightarrow{e_3}$ のなす角をそれぞれ求めよ.
- (2)
- すべての平面ベクトル $\vec a\,(\neq \vec 0),$ $\vec p$ に対して \[ |\vec a-\vec p| \geqq |\vec a|-\frac{\vec a}{|\vec a|}\cdot\vec p\] が成り立つことを示せ.
- (3)
- すべての内角が $120^\circ$ 未満である $\triangle\mathrm{ABC}$ において, 内部の点 $\mathrm P$ から各頂点までの距離の和 $L = |\overrightarrow{\mathrm{PA}}|+|\overrightarrow{\mathrm{PB}}|+|\overrightarrow{\mathrm{PC}}|$ が最小になるとき, 点 $\mathrm P$ はどのような位置にあるか.
(参考: $2000$ 東北大)
解答例
こちらを参照.
微分法 (理系)
問題《正方形の頂点の最小シュタイナー木問題》
$xy$ 平面上に $4$ 点 $\mathrm A(1,1),$ $\mathrm B(−1,1),$ $\mathrm C(−1,−1),$ $\mathrm D(1,−1)$ をとる.
また, $y$ 軸に関して対称になるように, $x$ 軸上に点 $\mathrm P,$ $\mathrm Q$ をとる.
このとき, $L = \mathrm{PQ}+\mathrm{PA}+\mathrm{QB}+\mathrm{QC}+\mathrm{PD}$ の最小値と, 最小値を与える点 $\mathrm P$ の座標を求めよ.
ただし, 点 $\mathrm P$ の $x$ 座標は $0$ 以上 $1$ 以下であるとする.
(参考: $2015$ 早稲田大)
解答例
こちらを参照.