タイル張り
定義と興味深い例
定義
正方形 $4$ 枚を組み合わせてできる次のような L 字型のタイル $1$ 枚の上に, 各辺の長さが半分で同じ形のタイル $4$ 枚を敷き詰めるにはどうすれば良いか.
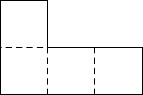 答え:
答え:
 このようなタイルは平面に隙間なく敷き詰めることができる.
上記の操作を無限に繰り返すと, フラクタル図形ができる(現実の世界では描けない).
$3$ 回目まで繰り返して一番小さいタイルに交互に色を塗ると次のようになる.
このようなタイルは平面に隙間なく敷き詰めることができる.
上記の操作を無限に繰り返すと, フラクタル図形ができる(現実の世界では描けない).
$3$ 回目まで繰り返して一番小さいタイルに交互に色を塗ると次のようになる.
 このフラクタル図形を上記のパズルの要領で同じ L 字型に敷き詰めたものは, $1$ 枚のフラクタル図形と相似になる.
このフラクタル図形を上記のパズルの要領で同じ L 字型に敷き詰めたものは, $1$ 枚のフラクタル図形と相似になる.



定義《タイリング》
平面に隙間なく敷き詰めることができるタイルは平面充填可能(tesselatable)であるという.
定義《レプタイル》
自身と等倍率で相似な $n$ 枚のタイルを使ってタイル張りできるタイルを $n$ レプタイル($n$-reptile)と呼ぶ.
ただし, $n \geqq 2$ とする.
これは自己複製タイル(replicating tile)の略語として, 爬虫類を意味する英語 reptile に語呂合わせして名付けられた.
定理《レプタイルの性質》
- (1)
- 任意の正整数 $e$ に対して, $n$ レプタイルは $n^e$ レプタイルである.
- (2)
- 任意のレプタイルはこのようなタイルは平面充填可能である.
- (3)
- レプタイルを用いてフラクタル図形を構成できる.
レプタイルの種類
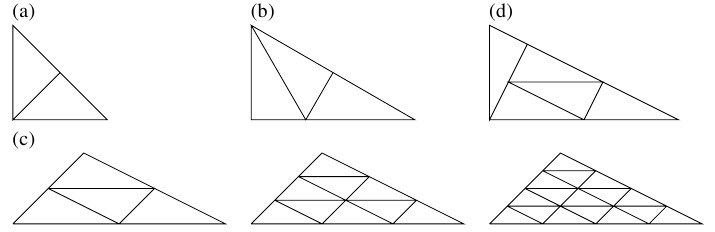
【三角形のレプタイル】
- (a)
- 直角二等辺三角形(三角定規の一方)は $2$ レプタイル.
- (b)
- 辺長の比が $1:\sqrt 3:2$ の直角三角形(三角定規の他方)は $3$ レプタイル.
- (c)
- 任意の三角形は $4$ レプタイル. 任意の整数 $m \geqq 2$ に対して $1+\dots +(2m-1) = m^2$ レプタイルでもある.
- (d)
- 辺長の比が $1:2:\sqrt 5$ の直角三角形は $5$ レプタイル.
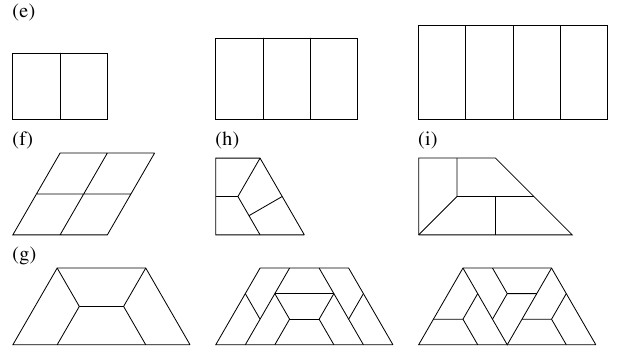
【四角形のレプタイル】
- (e)
- 辺長の比が $1:\sqrt n$ の長方形は $n$ レプタイル. 特に A 判の紙はすべて $2$ レプタイル.
- (f)
- 任意の平行四辺形(特に正方形やひし形)は $4$ レプタイル.
- (g)
- 正三角形 $3$ 個の辺を貼り合わせてできる等脚台形は $4$ レプタイル. $9$ レプタイルでもある.
- (h)
- 上記の等脚台形を $2$ 等分してできる直角台形は $4$ レプタイル.
- (i)
- 正方形と直角二等辺三角形の辺を貼り合わせてできる直角台形は $4$ レプタイル.
レプタイルはこの他にもたくさんある.
機会があれば紹介したい.
タイル張りの種類
レプタイル以外にも $1$ 種類の図形によるタイル張りの方法はたくさんある.
例えば, 次の定理を使えば様々なタイル張りが生み出せる.
定理《四面体タイル定理(秋山仁, 2007)》
正四面体の任意の展開図はタイル張り可能である.
つまり, 正四面体のどこか $1$ 箇所に切り込みを入れてばらばらにならないように注意しながらはさみで切り開けば, どのように切ってもタイル張り可能な図形が得られる.
辺に沿って切る必要はなく, 曲線状に切っても構わない.


Luzin の問題
大きさの異なる相似な図形への分割の問題も興味深い.
問題《Luzin の問題》
正方形を複数個の大きさが相異なる正方形に分割できるか.
この問題は 1907 年にイギリスの数学者・パズル作家の H. E. Dudeney によって提起され,
Dudeney は「カンタベリー・パズル」の中でこのような正方形の分割は不可能であると主張した.
その後, ロシアの数学者 N. Luzin も解なしと予想したが,
1938 年に正方形を 69 枚の正方形に分割する例が発見され,
1978 年には A. J. W. Duijvestijn によって分割に必要な正方形の個数は 21 枚以上であることが示された.
パズル
ここでは, 既知のタイル張りをもとに筆者が考案した興味深いパズルをいくつか紹介する.
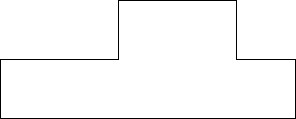
問題《ヘプトミノによる平面充填》
次の形のヘプトミノを $76$ 個使って長方形を作れ.
ただし, 裏返して使っても良い.

教材としてもおもしろいので, ルジンの問題の唯一の最小の解をパズルとして挙げておこう.
紙などで正方形のピースを作り, 実際に解いてみてほしい.
問題《Luzin の問題に関する正方形のパズル》
$1$ 辺の長さがそれぞれ $2,$ $4,$ $6,$ $7,$ $8,$ $9,$ $11,$ $15,$ $16,$ $17,$ $18,$ $19,$ $24,$ $25,$ $27,$ $29,$ $33,$ $35,$ $37,$ $42,$ $50$ の $21$ 枚の正方形を重ならないように隙間なく並べて $1$ 枚の正方形を作れ.
第 $1$ のヒント: 組み上がる正方形の $1$ 辺の長さは $112.$
第 $2$ のヒント: $27+35+50 = 33+37+42.$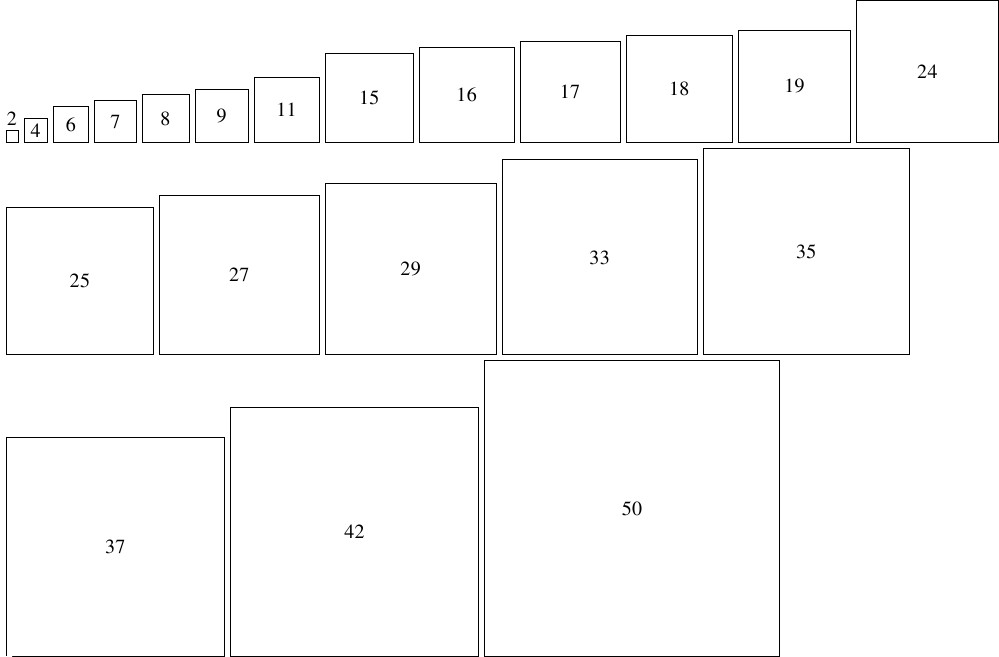
第 $2$ のヒント: $27+35+50 = 33+37+42.$
