有名問題・定理から学ぶ数学
Well-Known Problems and Theorems in Mathematics
数式を枠からはみ出さずに表示するためには, 画面を横に傾けてください.
頂点と五心がすべて有理点である三角形
§1 はじめに
- この記事は「日曜数学 Advent Calendar $2025$」の $18$ 日目の記事として書かれたものです.
- $17$ 日目の記事は, 上岡詩季 (FoxQ) @ゆるふわ 20 刀流さんの『数学の未来予想:AIの進化で数学は「誰でもで楽しめる」身近なものになるだろうか?』でした.
こんにちは. 廣津孝です. 皆さんとともに数学を通してクリスマスのお祝いができることを大変うれしく思います.
この記事では, $2023$ 年の記事, $2022$ 年の記事でご紹介した, 座標平面における
角の有理二等分問題 (Rational angle bisection problem)
どのような有理数 $a,$ $b$ に対して, 傾きが $a,$ $b$ である $2$ 直線のなす角の二等分線の傾きは有理数になるか
の応用として, 座標平面において
問題 1
有理点を結ぶ三角形のうち, どのような三角形に対して, 五心 (重心, 外心, 垂心, 内心, 傍心) は有理点になるか
という問題を考えます.
$xy$ 平面において, 有理点 (rational point) とは $x$ 座標も $y$ 座標も有理数であるような点です.
有理点のうち, $x$ 座標も $y$ 座標も整数であるような点を格子点 (lattice point) と呼ぶのでした.
問題 1 は, 三角形の五心に関する高校生向けの教材を作成しているときに, “頂点と五心がすべて格子点であるような三角形があれば作図がしやすくて便利だな” と思ったことから生まれました. 素朴な問題ですが, 内心, 傍心に関する部分は「角の有理二等分問題」の応用として解ける, 数論的に興味深い問題であることがわかったので, ここで紹介させていただきます.
問題 1 は, 三角形の五心に関する高校生向けの教材を作成しているときに, “頂点と五心がすべて格子点であるような三角形があれば作図がしやすくて便利だな” と思ったことから生まれました. 素朴な問題ですが, 内心, 傍心に関する部分は「角の有理二等分問題」の応用として解ける, 数論的に興味深い問題であることがわかったので, ここで紹介させていただきます.
§2 体上の三角形の面積と重心座標
まず, 有理点を結ぶ三角形において, 明らかに重心は有理点になります.
実は, このような三角形においては無条件で外心, 垂心も有理点になり, それは重心が有理点になることと同じ方法で証明できます.
せっかくなので, $k$ を実数体 $\mathbb R$ の部分体として, 次の概念を用いて一般的に議論を進めることにします.
$k/\mathbb Q$ が代数拡大の場合 (この場合が数論的に興味深い), $O_k$ を $k$ の整数環とします.
ピンとこない方は, $k$ が有理数体 $\mathbb Q,$ $O_k$ が通常の整数環 $\mathbb Z$ だと思って読み進めていただいても大丈夫です.
定義 1
- (1)
- 座標平面上の点 $\mathrm P(x,y)$ は, $\mathrm P \in k^2$ つまり $x,$ $y \in k$ のとき, $k$ 有理点 ($k$-rational point) であるという.
- (2)
- 座標平面上の多角形は, すべての頂点が $k$ 有理点であるとき, $k$ 上の多角形 (polygon over $k$) であるという.
- (1)'
- 座標平面上の点 $\mathrm P(x,y)$ は, $\mathrm P \in O_k{}^2$ つまり $x,$ $y \in O_k$ のとき, $k$ 格子点 ($k$-lattice point) であるという.
- (2)'
- 座標平面上の多角形は, すべての頂点が $k$ 格子点であるとき, $k$ 上の格子多角形 (lattice polygon over $k$) であるという.
$k$ 上の三角形については, 次の定理が基本的です.
定理 1
座標平面において, $k$ 上の $\triangle\mathrm{ABC}$ の面積 $S$ は $k$ に属する.
【定理 1 の証明】
平行移動しても面積は変わらないので, $\mathrm C$ が原点であるとしても一般性を失いません.
このとき, 残りの点の座標を $\mathrm A(a_1,a_2),$ $\mathrm B(b_1,b_2)$ とすると, 面積 $S$ は
\[ S = \frac{1}{2}|a_1b_2-a_2b_1|\]
と表されるので, $S$ は $k$ に属します. ■
$k$ 上の $\triangle\mathrm{ABC}$ の中心が $k$ 有理点であるかどうかは, 次の概念を使うと, 多くの場合に簡単に判定できます.
定義 2
平面 $\mathrm{ABC}$ 上の点 $\mathrm P$ に対して, $\triangle\mathrm{PBC},$ $\triangle\mathrm{PCA},$ $\triangle\mathrm{PAB}$ の面積比をかっこでくくったもの
\[ (\triangle\mathrm{PBC}:\triangle\mathrm{PCA}:\triangle\mathrm{PAB})\]
を ($\triangle\mathrm{ABC}$ に関する) $\mathrm P$ の重心座標 (barycentric coordinates) と呼ぶ.
ただし, ここでは $3$ 点 $\mathrm X,$ $\mathrm Y,$ $\mathrm Z$ が
- 一直線上に並ぶとき $\triangle\mathrm{XYZ}$ の面積は $0,$
- 反時計周りに並んで三角形の頂点となるとき $\triangle\mathrm{XYZ}$ の面積は正,
- 順時計回りに並んで三角形の頂点となるとき $\triangle\mathrm{XYZ}$ の面積は負
$\triangle\mathrm{ABC}$ の五心の重心座標の公式は, 次の通りです.
以下, $\mathrm{BC} = a,$ $\mathrm{CA} = b,$ $\mathrm{AB} = c,$ $a+b+c = 2s$ とします.
定理 2
$\triangle\mathrm{ABC}$ の重心 $\mathrm G,$ 外心 $\mathrm E,$ 垂心 $\mathrm H,$ 内心 $\mathrm I,$ $\angle\mathrm A$ 内の傍心 $\mathrm I_{\mathrm A},$ $\angle\mathrm B$ 内の傍心 $\mathrm I_{\mathrm B},$ $\angle\mathrm C$ 内の傍心 $\mathrm I_{\mathrm C},$ Gergonne 点 $\mathrm{Ge},$※1 Nagel 点 $\mathrm{Na}$※2 の重心座標は
\[\begin{aligned}
\mathrm G &= (1:1:1), \\
\mathrm E &= (a^2(b^2+c^2-a^2):b^2(c^2+a^2-b^2):c^2(a^2+b^2-c^2)), \\
\mathrm H &= \left(\frac{1}{b^2+c^2-a^2}:\frac{1}{c^2+a^2-b^2}:\frac{1}{a^2+b^2-c^2}\right), \\
\mathrm I &= (a:b:c), \\
\mathrm I_{\mathrm A} &= (-a:b:c), \\
\mathrm I_{\mathrm B} &= (a:-b:c), \\
\mathrm I_{\mathrm C} &= (a:b:-c), \\
\mathrm{Ge} &= \left(\frac{1}{s-a}:\frac{1}{s-b}:\frac{1}{s-c}\right), \\
\mathrm{Na} &= (s-a:s-b:s-c)
\end{aligned}\]
で与えられる.
- ※1:
- $\triangle\mathrm{ABC}$ と内接円が辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ 上の点 $\mathrm A',$ $\mathrm B',$ $\mathrm C'$ でそれぞれ接するとき, $3$ 直線 $\mathrm{AA}',$ $\mathrm{BB}',$ $\mathrm{CC}'$ は $1$ 点で交わることが知られており, その交点は Gergonne 点と呼ばれます.
- ※2:
- $\triangle\mathrm{ABC}$ と $\angle\mathrm A,$ $\angle\mathrm B,$ $\angle\mathrm C$ 内の傍接円が辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ 上の点 $\mathrm A'',$ $\mathrm B'',$ $\mathrm C''$ でそれぞれ接するとき, $3$ 直線 $\mathrm{AA}'',$ $\mathrm{BB}'',$ $\mathrm{CC}''$ は $1$ 点で交わることが知られており, その交点は Nagel 点と呼ばれます.
重心座標は, 次のように特徴付けられます.
定理 3
$\triangle\mathrm{ABC}$ の頂点の位置ベクトルが $\mathrm A(\vec a),$ $\mathrm B(\vec b),$ $\mathrm C(\vec c)$ であるとき, 平面 $\mathrm{ABC}$ 上の点 $\mathrm P(\vec p)$ に対して,
が成り立つ.
| $\mathrm P$ の重心座標が $(\lambda :\mu :\nu )$ $\iff$ $\vec p = \dfrac{\lambda\vec a+\mu\vec b +\nu\vec c}{\lambda +\mu +\nu}$ |
与えられた点が $k$ 有理点であるかどうかは, 次の定理を使って判定できます.
定理 4
座標平面において, $k$ 上の $\triangle\mathrm{ABC}$ に関して, 点 $\mathrm P$ に対して,
が成り立つ.
| $\mathrm P$ が $k$ 有理点 | |
| $\iff$ | $\mathrm P$ の重心座標 $(\lambda :\mu :\nu )$ が |
| $\dfrac{\lambda}{\lambda +\mu +\nu},$ $\dfrac{\mu}{\lambda +\mu +\nu},$ $\dfrac{\nu}{\lambda +\mu +\nu} \in k$ | |
| を満たすようにとれる |
【定理 4 の証明】
$\triangle\mathrm{PBC},$ $\triangle\mathrm{PCA},$ $\triangle\mathrm{PAB}$ の符号付き面積がそれぞれ $\lambda,$ $\mu,$ $\nu$ であるとします.
$\mathrm P$ が $k$ 有理点であるならば, 定理 1 により $\lambda,$ $\mu,$ $\nu \in k$ であるので,
\[\frac{\lambda}{\lambda +\mu +\nu},\ \frac{\mu}{\lambda +\mu +\nu},\ \frac{\nu}{\lambda +\mu +\nu} \in k \quad \cdots [1]\]
が成り立ちます.
逆に, $\mathrm P$ の重心座標 $(\lambda :\mu :\nu )$ が $[1]$ を満たすようにとれるとき, $\mathrm O$ を原点として $\overrightarrow{\mathrm{OA}},$ $\overrightarrow{\mathrm{OB}},$ $\overrightarrow{\mathrm{OC}} \in k^2$ であるので, \[\overrightarrow{\mathrm{OP}} = \frac{\lambda\overrightarrow{\mathrm{OA}}+\mu\overrightarrow{\mathrm{OB}}+\nu\overrightarrow{\mathrm{OC}}}{\lambda +\mu +\nu}\] で定まる点 $\mathrm P$ は $k$ 有理点になります (定理 3 を使いました). ■
逆に, $\mathrm P$ の重心座標 $(\lambda :\mu :\nu )$ が $[1]$ を満たすようにとれるとき, $\mathrm O$ を原点として $\overrightarrow{\mathrm{OA}},$ $\overrightarrow{\mathrm{OB}},$ $\overrightarrow{\mathrm{OC}} \in k^2$ であるので, \[\overrightarrow{\mathrm{OP}} = \frac{\lambda\overrightarrow{\mathrm{OA}}+\mu\overrightarrow{\mathrm{OB}}+\nu\overrightarrow{\mathrm{OC}}}{\lambda +\mu +\nu}\] で定まる点 $\mathrm P$ は $k$ 有理点になります (定理 3 を使いました). ■
注意 1
この定理は, $n$ 次元空間の $n$ 単体に対して一般化することができるが, $3$ 次元以上の空間内の三角形に対して一般化することはできない.
次の定理も有用です.
定理 5
座標平面において, $k$ 上の $\triangle\mathrm{ABC}$ に関して, 点 $\mathrm P$ の等長共役点※3
が $\mathrm Q$ であるとする.
このとき,
が成り立つ.
| $\mathrm P$ は $k$ 有理点 $\iff$ $\mathrm Q$ は $k$ 有理点 |
- ※3:
- $\triangle\mathrm{ABC}$ と点 $\mathrm P$ に対して, $\mathrm A,$ $\mathrm B,$ $\mathrm C$ を通る中線に関してそれぞれ $\mathrm{AP},$ $\mathrm{BP},$ $\mathrm{CP}$ と対称な $3$ 直線は $1$ 点で交わることが知られており, その交点は $\mathrm P$ の ($\triangle\mathrm{ABC}$ に関する) 等長共役点 (isotomic point) と呼ばれます. 例えば, $\triangle\mathrm{ABC}$ の Gergonne 点と Nagel 点は互いに等長共役点であることが知られています.
【定理 5 の証明】
$\mathrm P$ が正規化された重心座標 $(\lambda :\mu :\nu )$ をもつとします.
このとき, $\mathrm Q$ は重心座標 $\left(\dfrac{1}{\lambda}:\dfrac{1}{\mu}:\dfrac{1}{\nu}\right)$ をもつので (証明は割愛します),
\[\begin{aligned}
\mathrm P \in k^2 &\Longrightarrow \lambda,\ \mu,\ \nu \in k \\
&\Longrightarrow \frac{1}{\lambda},\ \frac{1}{\mu},\ \frac{1}{\nu} \in k \\
&\Longrightarrow \mathrm Q \in k^2
\end{aligned}\]
が成り立ちます.
逆に, $\mathrm P$ は $\mathrm Q$ の等長共役点であるので, $\mathrm Q \in k^2$ $\Longrightarrow$ $\mathrm P \in k^2$ も成り立ちます.
■
§3 重心, 外心, 垂心
§2 で予告していた通り, 次の定理が成り立ちます.
定理 6
座標平面において, $k$ 上の $\triangle\mathrm{ABC}$ の重心 $\mathrm G,$ 外心 $\mathrm E,$ 垂心 $\mathrm H$ は $k$ 有理点である.
【定理 6 の証明】
$a^2,$ $b^2,$ $c^2 \in k$ であるので, 定理 2 の $\mathrm G,$ $\mathrm E,$ $\mathrm H$ の重心座標の各成分は $k$ に属します.
よって, $\mathrm G,$ $\mathrm E,$ $\mathrm H$ は $k$ 有理点です. ■
注意 2
この定理の証明と同じ理由で, $k$ 上の $\triangle\mathrm{ABC}$ において, 他にも多くの中心が自動的に $k$ 有理点になる.
例えば, 九点円の中心などは, 重心座標が $a^2,$ $b^2,$ $c^2$ の多項式で表されるため, $k$ 有理点になる.
§4 角の有理二等分問題
いよいよ, 本題に入ります.
三角形の内心は $3$ つの内角の二等分線の交点, 傍心は $1$ つの内角と $2$ つの外角の二等分線の交点として定義されるのでした.
そこで, §1 で紹介した角の有理二等分問題を, より扱いやすい形に言い換えて再考します.
ここまでは平面図形のみを考えてきましたが, 角の二等分は高次元でもできるので, 見通しをよくするため, $n \geqq 2$ として $n$ 次元空間における角の二等分について述べます.
問題 2: 角の有理二等分問題・改
どのようなベクトル $\vec a,$ $\vec b \in k^n$ に対して, 方向ベクトルが $\vec a,$ $\vec b$ である $2$ 直線のなす角の二等分線の方向ベクトルは $k^n$ の中にとれるか.
$k/\mathbb Q$ が代数拡大の場合, 問題 2 は次の問題に帰着されます.
問題 2'
どのようなベクトル $\vec a,$ $\vec b \in O_k{}^n$ に対して, 方向ベクトルが $\vec a,$ $\vec b$ である $2$ 直線のなす角の二等分線の方向ベクトルは $O_k{}^n$ の中にとれるか.
これらの問題を解くうえで重要な役割を果たすのが, 次の定理です.
ここで, $a,$ $b \in k^\times$ に対して, $\dfrac{a}{b}$ が $k$ における平方数である, つまり $\dfrac{a}{b}$ が $k$ の乗法群 $k^\times = \{ q \in k \mid q \neq 0\}$ の部分群 $k^{\times 2} = \{ q^2 \mid q \in k^\times\}$ に属することを $a \equiv b \pmod{k^{\times 2}}$ で表し, $a,$ $b$ は $k^{\times 2}$ を法として合同 (congruent modulo $k^{\times 2}$) であるということにします.
定理 7
$\vec a,$ $\vec b$ を $k^n$ に属する線形独立なベクトルとする.
- (1)
- 次の条件は同値である.
- (A1)
- $\vec a,$ $\vec b$ を方向ベクトルとする $2$ 直線のなす角の二等分線の方向ベクトルとして $\vec c \in k^n$ がとれる.
- (A2)
- $\vec a,$ $\vec b$ を法線ベクトルとする $2$ つの超平面のなす角を二等分する超平面の法線ベクトルとして $\vec c \in k^n$ がとれる.
- (A3)
- \[ (\vec a\cdot\vec c) ^2|\vec b|^2 = (\vec b\cdot\vec c)^2|\vec a|^2 \quad \cdots [*]\] を満たすベクトル $\vec c \in k^n$ が存在する.
- (A4)
- \[ |\vec a|^2 \equiv |\vec b|^2 \pmod{k^{\times 2}}\] が成り立つ.
- (2)
- $k/\mathbb Q$ が代数拡大で, $\vec a = (a_1,\cdots,a_n),$ $\vec b = (b_1,\cdots,b_n) \in O_k{}^n$ であるとする.
このとき, 次の条件は同値である.
- (B1)
- $\vec a,$ $\vec b$ を方向ベクトルとする $2$ 直線のなす角の二等分線の方向ベクトルとして $\vec c \in O_k{}^n$ がとれる.
- (B2)
- $\vec a,$ $\vec b$ を法線ベクトルとする $2$ つの超平面のなす角を二等分する超平面の法線ベクトルとして $\vec c \in O_k{}^n$ がとれる.
- (B3)
- $[\ast ]$ を満たすベクトル $\vec c \in O_k{}^n$ が存在する.
- (B4)
- $d$ が正の数であり, $(x_1,\cdots,x_n,x_{n+1}) = (a_1,\cdots,a_n,a_{n+1}),$ $(b_1,\cdots,b_n,b_{n+1})$ が \[\sum_{i = 1}^nx_i{}^2 = dx_{n+1}{}^2 \quad \cdots [\ast\ast ]\] の解であるような代数的整数 $d,$ $a_{n+1},$ $b_{n+1} \in O_k$ が存在する.
【定理 7 の証明】
- (1)
- (A1) $\iff$ (A2) は, $2$ つの超平面のなす角の大きさが法線ベクトルのなす角の大きさとして定義されることから従います.
(A1) $\iff$ (A3) を示します. $\mathrm O \in \mathbb R^n,$ $\mathrm A_+,$ $\mathrm B,$ $\mathrm C \in \mathbb R^n\setminus\{\mathrm O\}$ として, $\vec a = \overrightarrow{\mathrm{OA}_+},$ $\vec b = \overrightarrow{\mathrm{OB}},$ $\vec c = \overrightarrow{\mathrm{OC}}$ とします. また, $\mathrm A_-$ を $\mathrm O$ に関して $\mathrm A_+$ と対称な点とします. $\angle\mathrm A_+\mathrm{OC} = \angle\mathrm{BOC}$ または $\angle\mathrm A_-\mathrm{OC} = \angle\mathrm{BOC}$ が成り立つことは, \[\begin{aligned} \frac{(\pm\vec a)\cdot\vec c}{|\pm\vec a||\vec c|} &= \frac{\vec b\cdot\vec c}{|\vec b||\vec c|}, \\ \pm\frac{\vec a\cdot\vec c}{|\vec a||\vec c|} &= \frac{\vec b\cdot\vec c}{|\vec b||\vec c|}, \end{aligned}\] よって $[\ast ]$ と同値です ($[\ast ]$ は両辺に $|\vec a||\vec b||\vec c|$ を掛け, 両辺を $2$ 乗すると得られます).
また, 明らかに (A3) $\Longrightarrow$ (A4) が成り立ちます. 逆に, (A4) が成り立つとき, $\vec c = \vec a\pm\dfrac{|\vec a|}{|\vec b|}\vec b$ は $[\ast ]$ を満たすので, (A3) が成り立ちます. - (2)
- (1) と同様の議論により, (B1)~(B3) は同値であることが示せます.
$[\ast ]$ を満たすベクトル $\vec c \in O_k{}^n$ の存在を仮定します. このとき, $|\vec a|^2 \equiv |\vec b|^2 \pmod{k^{\times 2}}$ であるので, $d$ が正の数であり, \[ |\vec a|^2 = da_{n+1}{}^2, \quad |\vec b|^2 = db_{n+1}{}^2\] を満たす代数的整数 $d,$ $a_{n+1},$ $b_{n+1} \in O_k$ が存在します. これは, $(x_1,\cdots,x_n,x_{n+1}) = (a_1,\cdots,a_n,a_{n+1}),$ $(b_1,\cdots,b_n,b_{n+1})$ が $[\ast\ast ]$ の解であることを意味します. また, この逆も成り立ちます. ■
例 1
$\vec a = (a_1,\cdots,a_n),$ $\vec b = (b_1,\cdots,b_n) \in k^n$ とする.
\[\{ |b_1|,\cdots,|b_n|\} = \{ q|a_1|,\cdots,q|a_n|\}\]
または
\[\{ |a_1|,\cdots,|a_n|\} = \{ q|b_1|,\cdots,q|b_n|\}\]
を満たす $0$ 以上の数 $q \in k$ が存在するならば, $\vec a,$ $\vec b,$ $\vec c = \vec a$ は $[\ast ]$ を満たす.
このような解を $[\ast ]$ の自明解 (trivial solution) と呼ぶ.
$n = 2,$ $k = \mathbb Q$ の場合の問題 2 の解は $2023$ 年の記事でたくさん扱っているので, ここでは $[\ast ]$ の非自明解から生じる例を紹介します.
例 2
- (1)
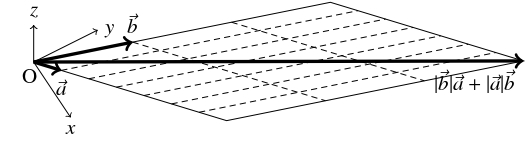
- $\vec a = (2,1,1),$ $\vec b = (3,6,2)$ を方向ベクトルとする $2$ 直線のなす角の二等分線として方向ベクトル $7\vec a\pm 3\vec b$ がとれる. これは, $|\vec a| = 3,$ $|\vec b| = 7$ であり, $7\vec a,$ $3\vec b$ がひし形を張ることからわかる.
- (2)
- $\vec a = (1,1,4),$ $\vec b = (3,4,5)$ を方向ベクトルとする $2$ 直線のなす角の二等分線として方向ベクトル $5\vec a\pm 3\vec b$ がとれる. これは, $|\vec a| = 3\sqrt 2,$ $|\vec b| = 5\sqrt 2$ であり, $5\vec a,$ $3\vec b$ がひし形を張ることからわかる.
§5 内心, 傍心が有理点になる条件
少し脱線してしまったので, 平面上の三角形の話に戻りましょう.
次の定理の主張では, 次の概念を使います.
定義 3
座標平面上の三角形は, $3$ 辺の長さと面積が $k$ に属するとき, $k$ 上の Heron の三角形 (Heronian triangle over $k$) であるという.
定理 8
座標平面上にある $k$ 上の $\triangle\mathrm{ABC}$ において, $\mathrm{BC} = a,$ $\mathrm{CA} = b,$ $\mathrm{AB} = c$ とし, 内接円の半径を $r,$ 傍接円の半径を $r_{\mathrm A},$ $r_{\mathrm B},$ $r_{\mathrm C}$ とおく.
このとき, 次の条件は同値である.
- (T1)
- $\triangle\mathrm{ABC}$ の内心 $\mathrm I,$ 傍心 $\mathrm I_{\mathrm A},$ $\mathrm I_{\mathrm B},$ $\mathrm I_{\mathrm C},$ Gergonne 点 $\mathrm{Ge},$ Nagel 点 $\mathrm{Na}$ の少なくとも $1$ つは $k$ 有理点である.
- (T2)
- \[ a^2 \equiv b^2 \equiv c^2 \pmod{k^{\times 2}} \quad \cdots [\ast\ast\ast ]\] が成り立つ.
【定理 8 の証明】
(T1) $\Longrightarrow$ (T2) は, $\mathrm I$ が $3$ つの内角の二等分線の交点であることから, 定理 7 により従います.
(T2) $\Longrightarrow$ (T1) の証明には, 定理 2 の重心座標の公式を使います. $[\ast\ast\ast ]$ が成り立つならば, $a = a_0\sqrt d,$ $b = b_0\sqrt d,$ $c = c_0\sqrt d$ を満たす正の数 $a_0,$ $b_0,$ $c_0,$ $d \in k$ が存在して \[ 2s = (a_0+b_0+c_0)\sqrt d\] となるので, \[\frac{a}{2s} = \frac{a_0}{a_0+b_0+c_0},\ \frac{b}{2s} = \frac{b_0}{a_0+b_0+c_0},\ \frac{c}{2s} = \frac{c_0}{a_0+b_0+c_0} \in k\] となり, $\mathrm I \in k^2$ となります.
\[\begin{aligned} \frac{a}{2s}-\frac{a}{2(s-a)} &= \frac{1}{2}, \\ \frac{b}{2s}-\frac{b}{2(s-a)} &= \frac{b}{2a}, \quad \frac{c}{2s}-\frac{c}{2(s-a)} = \frac{c}{2a} \end{aligned}\] に注意すると, \[\begin{aligned} \mathrm I \in k^2 &\iff \frac{a}{2s},\ \frac{b}{2s},\ \frac{c}{2s} \in k \\ &\iff -\frac{a}{2(s-a)},\ \frac{b}{2(s-a)},\ \frac{c}{2(s-a)} \in k \\ &\iff \mathrm I_{\mathrm A} \in k^2 \end{aligned}\] であることがわかります. 同様に, $\mathrm I \in k^2 \iff \mathrm I_{\mathrm B} \in k^2,$ および $\mathrm I \in k^2 \iff \mathrm I_{\mathrm C} \in k^2$ が成り立ちます. また, \[ (s-a)+(s-b)+(s-c) = s\] に注意すると, \[\begin{aligned} \mathrm I \in k^2 &\iff \frac{a}{2s},\ \frac{b}{2s},\ \frac{c}{2s} \in k \\ &\iff \frac{s-a}{s},\ \frac{s-b}{s},\ \frac{s-c}{s} \in k \\ &\iff \mathrm{Na} \in k^2 \end{aligned}\] であることがわかります. さらに, $\mathrm{Ge},$ $\mathrm{Na}$ は互いに等長共役の関係にあるので, 定理 5 により \[\mathrm{Ge} \in k^2 \iff \mathrm{Na} \in k^2\] が成り立ちます. さらに, $[\ast\ast\ast ]$ が成り立つとき, 上記の正の数 $a_0,$ $b_0,$ $c_0,$ $d \in k$ に対して \[\begin{aligned} 2(s-a) &= (b_0+c_0-a_0)\sqrt d, \\ 2(s-b) &= (c_0+a_0-b_0)\sqrt d, \\ 2(s-c) &= (a_0+b_0-c_0)\sqrt d \end{aligned}\] となるので, $\triangle\mathrm{ABC}$ の面積 $S$ と $r,$ $r_{\mathrm A},$ $r_{\mathrm B},$ $r_{\mathrm C}$ の関係式 \[ S = rs = r_{\mathrm A}(s-a) = r_{\mathrm B}(s-b) = r_{\mathrm C}(s-c)\] (こちらを参照) により $r^2,$ $r_{\mathrm A}{}^2,$ $r_{\mathrm B}{}^2,$ $r_{\mathrm C}{}^2$ は $k^\times$ の元であり, \[ r^2 \equiv r_{\mathrm A}{}^2 \equiv r_{\mathrm B}{}^2 \equiv r_{\mathrm C}{}^2 \equiv d \pmod{k^{\times 2}}\] が成り立ちます. このことは, $\triangle\mathrm{ABC}$ が $k$ 上の Heron の三角形 ($3$ 辺の長さが $a_0,$ $b_0,$ $c_0,$ 面積が $\dfrac{S}{d}$) を $\sqrt d$ 倍に拡大して得られることを意味します. ■
(T2) $\Longrightarrow$ (T1) の証明には, 定理 2 の重心座標の公式を使います. $[\ast\ast\ast ]$ が成り立つならば, $a = a_0\sqrt d,$ $b = b_0\sqrt d,$ $c = c_0\sqrt d$ を満たす正の数 $a_0,$ $b_0,$ $c_0,$ $d \in k$ が存在して \[ 2s = (a_0+b_0+c_0)\sqrt d\] となるので, \[\frac{a}{2s} = \frac{a_0}{a_0+b_0+c_0},\ \frac{b}{2s} = \frac{b_0}{a_0+b_0+c_0},\ \frac{c}{2s} = \frac{c_0}{a_0+b_0+c_0} \in k\] となり, $\mathrm I \in k^2$ となります.
\[\begin{aligned} \frac{a}{2s}-\frac{a}{2(s-a)} &= \frac{1}{2}, \\ \frac{b}{2s}-\frac{b}{2(s-a)} &= \frac{b}{2a}, \quad \frac{c}{2s}-\frac{c}{2(s-a)} = \frac{c}{2a} \end{aligned}\] に注意すると, \[\begin{aligned} \mathrm I \in k^2 &\iff \frac{a}{2s},\ \frac{b}{2s},\ \frac{c}{2s} \in k \\ &\iff -\frac{a}{2(s-a)},\ \frac{b}{2(s-a)},\ \frac{c}{2(s-a)} \in k \\ &\iff \mathrm I_{\mathrm A} \in k^2 \end{aligned}\] であることがわかります. 同様に, $\mathrm I \in k^2 \iff \mathrm I_{\mathrm B} \in k^2,$ および $\mathrm I \in k^2 \iff \mathrm I_{\mathrm C} \in k^2$ が成り立ちます. また, \[ (s-a)+(s-b)+(s-c) = s\] に注意すると, \[\begin{aligned} \mathrm I \in k^2 &\iff \frac{a}{2s},\ \frac{b}{2s},\ \frac{c}{2s} \in k \\ &\iff \frac{s-a}{s},\ \frac{s-b}{s},\ \frac{s-c}{s} \in k \\ &\iff \mathrm{Na} \in k^2 \end{aligned}\] であることがわかります. さらに, $\mathrm{Ge},$ $\mathrm{Na}$ は互いに等長共役の関係にあるので, 定理 5 により \[\mathrm{Ge} \in k^2 \iff \mathrm{Na} \in k^2\] が成り立ちます. さらに, $[\ast\ast\ast ]$ が成り立つとき, 上記の正の数 $a_0,$ $b_0,$ $c_0,$ $d \in k$ に対して \[\begin{aligned} 2(s-a) &= (b_0+c_0-a_0)\sqrt d, \\ 2(s-b) &= (c_0+a_0-b_0)\sqrt d, \\ 2(s-c) &= (a_0+b_0-c_0)\sqrt d \end{aligned}\] となるので, $\triangle\mathrm{ABC}$ の面積 $S$ と $r,$ $r_{\mathrm A},$ $r_{\mathrm B},$ $r_{\mathrm C}$ の関係式 \[ S = rs = r_{\mathrm A}(s-a) = r_{\mathrm B}(s-b) = r_{\mathrm C}(s-c)\] (こちらを参照) により $r^2,$ $r_{\mathrm A}{}^2,$ $r_{\mathrm B}{}^2,$ $r_{\mathrm C}{}^2$ は $k^\times$ の元であり, \[ r^2 \equiv r_{\mathrm A}{}^2 \equiv r_{\mathrm B}{}^2 \equiv r_{\mathrm C}{}^2 \equiv d \pmod{k^{\times 2}}\] が成り立ちます. このことは, $\triangle\mathrm{ABC}$ が $k$ 上の Heron の三角形 ($3$ 辺の長さが $a_0,$ $b_0,$ $c_0,$ 面積が $\dfrac{S}{d}$) を $\sqrt d$ 倍に拡大して得られることを意味します. ■
§6 三角形の構成法
定理 8 から, 次の三角形の構成法が得られます.
定理 9
$k/\mathbb Q$ が代数拡大であるとき, 内心が $k$ 有理点である (このとき必然的に傍心, Gergonne 点, Nagel 点も $k$ 有理点になる) ような $k$ 上の $\triangle\mathrm{ABC}$ はすべて, 次の方法で構成できる.
- (1)
- 正の代数的整数 $d \in O_k$ を選ぶ.
- (2)
- $\vec p = (p_1,p_2),$ $\vec q = (q_1,q_2),$ $\vec r = (r_1,r_2)$ が対ごとに線形独立となるように $x_1{}^2+x_2{}^2 = dx_3{}^2$ の解 $(x_1,x_2,x_3) = (p_1,p_2,p_3),$ $(q_1,q_2,q_3),$ $(r_1,r_2,r_3) \in O_k{}^3$ を選ぶ.
- (3)
- 点 $\mathrm B_0(r_1,r_2)$ を通り $\vec p$ を方向ベクトルとする直線, 原点 $\mathrm O$ と点 $(q_1,q_2)$ を結ぶ直線の交点 $\mathrm C_0$ を求め, $\triangle\mathrm{OB}_0\mathrm C_0$ を作る.
- (4)
- $\triangle\mathrm{OB}_0\mathrm C_0$ を適当な倍率に拡大し, 必要に応じて平行移動したものを $\triangle\mathrm{ABC}$ とする.
【定理 9 の証明】
$k$ 上の $\triangle\mathrm{ABC}$ の内心が $k$ 有理点であるとします.
- (i)
- $\triangle\mathrm{ABC}$ が $k$ 上の格子三角形である場合. $\vec p = \overrightarrow{\mathrm{BC}},$ $\vec q = \overrightarrow{\mathrm{CA}},$ $\vec r = \overrightarrow{\mathrm{AB}}$ とおきます. このとき, 三角形が成立することから, $\vec p,$ $\vec q,$ $\vec r$ は対ごとに線形独立になります. また, 定理 8 により \[ |\vec p|^2 \equiv |\vec q|^2 \equiv |\vec r|^2 \pmod{k^{\times 2}}\] が成り立つので, $d > 0$ であり, $(x_1,x_2,x_3) = (p_1,p_2,p_3),$ $(q_1,q_2,q_3),$ $(r_1,r_2,r_3)$ が $x_1{}^2+x_2{}^2 = dx_3{}^2$ の解であるような代数的整数 $p_3,$ $q_3,$ $r_3,$ $d \in O_k$ が存在します. (3) の方法で得られる $\triangle\mathrm{OB}_0\mathrm C_0$ ($\mathrm B_0,$ $\mathrm C_0$ は $\overrightarrow{\mathrm{OB}_0} = \vec r,$ $\overrightarrow{\mathrm{OC}_0} = -\vec q$ で定まる点) を $\overrightarrow{\mathrm{OA}}$ だけ平行移動すると, $\triangle\mathrm{ABC}$ が得られます.
- (ii)
- 一般の場合. $\triangle\mathrm{ABC}$ は, 適当な倍率に拡大することによって $k$ 上の格子三角形で内心が $k$ 有理点であるものと相似になるので, (1)~(4) の方法で構成できます. ■
例えば,
- (i)
- $k = \mathbb Q,$ $d = 1$
- (ii)
- $k = \mathbb Q,$ $d = 2$
- (iii)
- $k = \mathbb Q(\sqrt 2),$ $d = 3$
例 3
次の場合に, $\triangle\mathrm{ABC}$ の重心 $\mathrm G,$ 外心 $\mathrm E,$ 垂心 $\mathrm H,$ 内心 $\mathrm I,$ 傍心 $\mathrm I_{\mathrm A},$ $\mathrm I_{\mathrm B},$ $\mathrm I_{\mathrm C},$ Gergonne 点 $\mathrm{Ge},$ Nagel 点 $\mathrm{Na}$ は $k$ 有理点になる.
参考のために, $k$ 上の Heron の三角形に対する相似比の $2$ 乗 $d$ と, $3$ 辺の長さ $a,$ $b,$ $c,$ 内接円の半径 $r,$ 傍接円の半径 $r_{\mathrm A},$ $r_{\mathrm B},$ $r_{\mathrm C},$ 面積 $S$ の値を付記しておく.
\[\begin{array}{|c||c|c|c|}\hline
{} & \text{(i)} & \text{(ii)} & \text{(iii)} \\ \hline
k & \mathbb Q & \mathbb Q & \mathbb Q(\sqrt 2) \\
d & 1 & 2 & 3 \\ \hline
\mathrm A & (0,0) & (0,0) & (0,0) \\
\mathrm B & (30,16) & (17,7) & (57,3\sqrt 2) \\
\mathrm C & (15,36) & (3,21) & (50,10\sqrt 2) \\ \hline
\mathrm G & \left(15,\frac{52}{3}\right) & \left(\frac{20}{3},\frac{28}{3}\right) & \left(\frac{107}{3},\frac{13}{3}\sqrt 2\right) \\
\mathrm E & \left(\frac{72}{7},\frac{943}{56}\right) & \left(\frac{47}{8},\frac{79}{8}\right) & \left(\frac{117}{4},-\frac{45}{8}\sqrt 2\right) \\
\mathrm H & \left(\frac{171}{7},\frac{513}{28}\right) & \left(\frac{33}{4},\frac{33}{4}\right) & \left(\frac{97}{2},\frac{97}{4}\sqrt 2\right) \\ \hline
\mathrm I & \left(\frac{120}{7},\frac{132}{7}\right) & (7,9) & (48,6\sqrt 2) \\
\mathrm I_{\mathrm A} & \left( 35,\frac{77}{2}\right) & (21,27) & (60,\frac{15}{2}\sqrt 2) \\
\mathrm I_{\mathrm B} & (-33,30) & (-18,14) & (15,-60\sqrt 2) \\
\mathrm I_{\mathrm C} & (22,-20) & \left(\frac{27}{2},-\frac{21}{2}\right) & (-6,24\sqrt 2) \\
\mathrm{Ge} & \left(\frac{96}{5},\frac{96}{5}\right) & \left(\frac{539}{73},\frac{637}{73}\right) & \left(\frac{5096}{103},\frac{784}{103}\sqrt 2\right) \\
\mathrm{Na} & \left(\frac{75}{7},\frac{100}{7}\right) & (6,10) & (11,\sqrt 2) \\ \hline
a & 25 & 14\sqrt 2 & 7\sqrt 3 \\
b & 39 & 15\sqrt 2 & 33\sqrt 3 \\
c & 34 & 13\sqrt 2 & 30\sqrt 3 \\
r & \frac{60}{7} & 4\sqrt 2 & 2\sqrt 6 \\
r_{\mathrm A} & \frac{35}{2} & 12\sqrt 2 & \frac{5}{2}\sqrt 6 \\
r_{\mathrm B} & 42 & 14\sqrt 2 & 35\sqrt 6 \\
r_{\mathrm C} & 28 & \frac{21}{2}\sqrt 2 & 14\sqrt 6 \\ \hline
S & 420 & 168 & 210\sqrt 2 \\ \hline
\end{array}\]
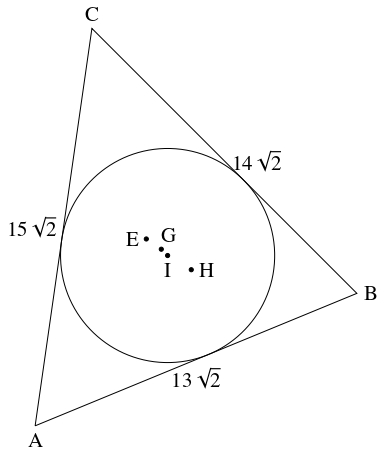
(ii) の $\triangle\mathrm{ABC}$ は次のような形の三角形である.
これは, Brahmagupta の三角形 ($3$ 辺の長さが $1$ ずつ異なる Heron の三角形) のうち最小の鋭角三角形 ($3$ 辺の長さが $13,$ $14,$ $15$) を $\sqrt 2$ 倍に拡大して得られる.

頂点と五心がすべて格子点であるような三角形は, 上記の方法で構成した $\mathbb Q$ 上の三角形を適当な倍率に拡大することで得られます.
参考文献
- [1]
- Takashi Hirotsu, General Pell's equations and angle bisectors between planar lines with rational slopes, Integers, 24 (2024), #A111.
- [2]
- Takashi Hirotsu, Rational angle bisection problem in higher dimensional spaces and incenters of simplices over fields, https://arxiv.org/abs/2512.24660
- [3]
- C. Kimberling, Encyclopedia of Triangle Centers, https://faculty.evansville.edu/ck6/encyclopedia/ETC.html (retrieved 15 Dec. 2025).
更新履歴
- 2025/12/18
- 公開, 修正, 加筆, 図の追加
- 2025/12/19
- 修正 (Gergonne 点の重心座標, 定理 8 の証明), 差し替え (定理 5 の内容と証明), 加筆 (定理 9 周辺)
- 2025/12/20
- 図の追加
- 2025/12/24
- 修正 (定理 9 の誤植)
- 2026/01/01
- 論文 [2] が arXiv で公開
お気づきの点などがありましたら, 以下の連絡先までお願いします.
- 氏 名
- 廣津 孝 (ひろつ たかし)
- (理学博士)
- メール