三角形の面積
三角形の面積
$\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C$ とおく.
定理《三角形の面積》
$\triangle\mathrm{ABC}$ の面積 $S$ は,
\[ S = \frac{1}{2}bc\sin A = \frac{1}{2}ca\sin B = \frac{1}{2}ab\sin C\]
である.
問題《三角形の面積》
- (A)
- $\mathrm{BC} = 7,$ $\mathrm{CA} = 5,$ $\mathrm{AB} = 3$ なる $\triangle\mathrm{ABC}$ の面積を求めよ.
- (B)
- $\mathrm{BC} = 7,$ $\mathrm{CA} = 5,$ $\mathrm{AB} = 8$ なる $\triangle\mathrm{ABC}$ の面積を求めよ.
解答例
- (A)
- \[\cos\angle\mathrm A = \frac{5^2+3^2-7^2}{2\cdot 5\cdot 3} = \frac{-15}{2\cdot 5\cdot 3} = -\frac{1}{2}\] から, $\angle\mathrm A = 120^\circ$ である. よって, $\triangle\mathrm{ABC}$ の面積は, \[\triangle\mathrm{ABC} = \frac{1}{2}\cdot 5\cdot 3\sin 120^\circ = \frac{1}{2}\cdot 5\cdot 3\cdot\frac{\sqrt 3}{2} = \frac{15\sqrt 3}{4}\] である.
- (B)
- \[\cos\angle\mathrm A = \frac{5^2+8^2-7^2}{2\cdot 5\cdot 8} = \frac{40}{2\cdot 5\cdot 8} = \frac{1}{2}\] から, $\angle\mathrm A = 60^\circ$ である. よって, $\triangle\mathrm{ABC}$ の面積は, \[\triangle\mathrm{ABC} = \frac{1}{2}\cdot 5\cdot 8\sin 60^\circ = \frac{1}{2}\cdot 5\cdot 8\cdot\frac{\sqrt 3}{2} = 10\sqrt 3\] である.
別解:「ヘロンの公式」を利用
- (A)
- $\triangle\mathrm{ABC}$ の半周長は $\dfrac{7+5+3}{2} = \dfrac{15}{2}$ であるから, 面積は「ヘロンの公式」(こちらを参照) により \[\begin{aligned} \triangle\mathrm{ABC} &= \sqrt{\frac{15}{2}\left(\frac{15}{2}-7\right)\left(\frac{15}{2}-5\right)\left(\frac{15}{2}-3\right)} \\ &= \frac{\sqrt{15(15-14)(15-10)(15-6)}}{4} \\ &= \frac{\sqrt{15\cdot 1\cdot 5\cdot 9}}{4} = \frac{15\sqrt 3}{4} \end{aligned}\] である.
- (B)
- $\triangle\mathrm{ABC}$ の半周長は $\dfrac{7+5+8}{2} = 10$ であるから, 面積は「ヘロンの公式」(こちらを参照) により \[\begin{aligned} \triangle\mathrm{ABC} &= \sqrt{10(10-7)(10-5)(10-8)} \\ &= \sqrt{10\cdot 3\cdot 5\cdot 2} = 10\sqrt 3 \end{aligned}\] である.
参考
- 各辺の長さが整数で, $1$ つの内角の大ささが $120^\circ$ である三角形の $3$ 辺の長さは, 余弦定理により $a^2+b^2+ab = c^2$ を満たす. この方程式の正の整数解を「アイゼンシュタインの $3$ つ組」と呼ぶ. すべての「アイゼンシュタインの $3$ つ組」は, 必要に応じて並べ替えると, 正の整数 $m,$ $n$ ($m,$ $n$ は互いに素, $3$ で割った余りが異なる, $m > n$) を用いて \[ (m^2-n^2,2mn+n^2,m^2+n^2+mn)\] の整数倍の形に表される. ここで, $m = 2,$ $n = 1$ とすると, (A) の三角形 (通称「七五三の三角形」) の $3$ 辺の長さが得られる.
- 各辺の長さが整数で, $1$ つの内角の大ささが $60^\circ$ である三角形の $3$ 辺の長さは, 余弦定理により $a^2+b^2-ab = c^2$ を満たす. この方程式の正の整数解を「半角アイゼンシュタインの $3$ つ組」と呼ぶ. すべての「半角アイゼンシュタインの $3$ つ組」は, 必要に応じて並べ替えると, 正の整数 $m,$ $n$ ($m,$ $n$ は互いに素, $3$ で割った余りが異なる, $m > 2n$) を用いて \[ (m^2-n^2,2mn-n^2,m^2+n^2-mn)\] または \[\left(\frac{m^2-n^2}{3},\frac{2mn-n^2}{3},\frac{m^2+n^2-mn}{3}\right)\] (場合分けの条件は $m+n$ が $3$ と互いに素か否か) の整数倍の形に表される. ここで, $m = 3,$ $n = 2$ とすると, (B) の三角形 (通称「名古屋の三角形」, 正三角形の次に非自明) の $3$ 辺の長さが得られる.
問題《角の二等分線の性質》
$\triangle\mathrm{ABC}$ において, $\angle\mathrm A$ の内角の二等分線と辺 $\mathrm{BC}$ の交点を $\mathrm D$ とおく.
\[\mathrm{BD}:\mathrm{DC} = \mathrm{AB}:\mathrm{AC}\]
が成り立つことを示せ.
解答例
$\theta = \angle\mathrm{BAC}$ とおくと, 三角形の面積の公式により
\[\begin{aligned}
\mathrm{BD}:\mathrm{DC} &= \triangle\mathrm{ABD}:\triangle\mathrm{ACD} \\
&= \frac{1}{2}\mathrm{AB}\cdot\mathrm{AD}\sin\frac{\theta}{2}:\frac{1}{2}\mathrm{AC}\cdot\mathrm{AD}\sin\frac{\theta}{2} \\
&= \mathrm{AB}:\mathrm{AC}
\end{aligned}\]
が得られる.
問題《複比の不変性》
点 $\mathrm O$ を始点とする半直線 $a,$ $b,$ $c,$ $d$ がそれぞれ,
直線 $l$ と相異なる $4$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm D$ で交わり,
直線 $l'$ と相異なる $4$ 点 $\mathrm A',$ $\mathrm B',$ $\mathrm C',$ $\mathrm D'$ で交わるとする.
- (1)
- 面積の比 $\dfrac{\triangle\mathrm{OAC}}{\triangle\mathrm{OBC}}$ を $2$ 本の線分の長さの比として表せ.
- (2)
- 面積の比 $\dfrac{\triangle\mathrm{OAC}}{\triangle\mathrm{OBC}}$ を $2$ 本の線分の長さ, $2$ つの角の三角比を用いて表せ.
- (3)
- \[\frac{\mathrm{AC}}{\mathrm{BC}}\cdot\frac{\mathrm{BD}}{\mathrm{AD}} = \frac{\mathrm A'\mathrm C'}{\mathrm B'\mathrm C'}\cdot\frac{\mathrm B'\mathrm D'}{\mathrm A'\mathrm D'}\] が成り立つことを示せ.
解答例
- (1)
- 三角形の面積の公式により, \[\begin{aligned} \dfrac{\triangle\mathrm{OAC}}{\triangle\mathrm{OBC}} &= \frac{\dfrac{1}{2}\mathrm{CO}\cdot\mathrm{CA}\sin\angle\mathrm{OCA}}{\dfrac{1}{2}\mathrm{CO}\cdot\mathrm{CB}\sin\angle\mathrm{OCB}} \\ &= \frac{\mathrm{AC}\sin\angle\mathrm{OCA}}{\mathrm{BC}\sin (180^\circ -\angle\mathrm{OCA})} \\ &= \frac{\mathrm{AC}}{\mathrm{BC}} \quad (\because\sin (180^\circ -\angle\mathrm{OCA}) = \sin\angle\mathrm{OCA}) \end{aligned}\] である.
- (2)
- 三角形の面積の公式により, \[\begin{aligned} \dfrac{\triangle\mathrm{OAC}}{\triangle\mathrm{OBC}} &= \frac{\dfrac{1}{2}\mathrm{OA}\cdot\mathrm{OC}\sin\angle\mathrm{AOC}}{\dfrac{1}{2}\mathrm{OB}\cdot\mathrm{OC}\sin\angle\mathrm{BOC}} \\ &= \frac{\mathrm{OA}\sin\angle\mathrm{AOC}}{\mathrm{OB}\sin\angle\mathrm{BOC}} \end{aligned}\] である.
- (3)
- (1), (2) の結果から, \[\frac{\mathrm{AC}}{\mathrm{BC}} = \frac{\mathrm{OA}\sin\angle\mathrm{AOC}}{\mathrm{OB}\sin\angle\mathrm{BOC}} \quad \cdots [1]\] が成り立つ. 同様に, \[\frac{\mathrm{AD}}{\mathrm{BD}} = \frac{\mathrm{OA}\sin\angle\mathrm{AOD}}{\mathrm{OB}\sin\angle\mathrm{BOD}} \quad \cdots [2]\] であるから, $[1]\div [2]$ から \[\frac{\mathrm{AC}}{\mathrm{BC}}\cdot\frac{\mathrm{BD}}{\mathrm{AD}} = \frac{\sin\angle\mathrm{AOC}\sin\angle\mathrm{BOD}}{\sin\angle\mathrm{BOC}\sin\angle\mathrm{AOD}}\] が得られる. この値は, $a,$ $b,$ $c,$ $d$ のなす角の大きさのみに依存し, $l$ を $a,$ $b,$ $c,$ $d$ と相異なる $4$ 点で交わる別の直線 $l'$ に取り換えても変わらない. つまり, \[\frac{\mathrm{AC}}{\mathrm{BC}}\cdot\frac{\mathrm{BD}}{\mathrm{AD}} = \frac{\mathrm A'\mathrm C'}{\mathrm B'\mathrm C'}\cdot\frac{\mathrm B'\mathrm D'}{\mathrm A'\mathrm D'}\] が成り立つ.
参考
点 $\mathrm O$ を始点とする半直線 $a,$ $b,$ $c,$ $d$ がそれぞれ, 直線 $l$ と相異なる $4$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm D$ で交わるとき, 線分の長さの比の比
\[\frac{\mathrm{AC}}{\mathrm{BC}}\div\frac{\mathrm{AD}}{\mathrm{BD}} = \frac{\mathrm{AC}}{\mathrm{BC}}\cdot\frac{\mathrm{BD}}{\mathrm{AD}}\]
を「複比」(cross ratio) と呼ぶ.
「複比」の概念は「射影幾何学」で重要な役割を果たす.
問題《ヘロンの三角形》
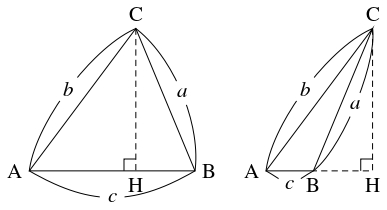
$\triangle\mathrm{ABC}$ の頂点 $\mathrm C$ から $\mathrm{AB}$ に下ろした垂線の足を $\mathrm H$ とおく.
- (1)
- $a,$ $b,$ $c$ と $S = \triangle\mathrm{ABC}$ を用いて, $\dfrac{\mathrm{AH}}{b},$ $\dfrac{\mathrm{BH}}{a},$ $\dfrac{\mathrm{CH}}{b}$ を表せ.
- (2)
- $a,$ $b,$ $c$ と $S$ が整数であるならば, $2c\cdot\mathrm{AH},$ $2c\cdot\mathrm{BH},$ $c\cdot\mathrm{CH}$ は整数であることを示せ.
解答例
- (1)
- 三角比の定義, 三角形の面積の公式, 余弦定理により,
\[\begin{aligned}
\frac{\mathrm{AH}}{b} &= |\cos A| = \frac{|b^2+c^2-a^2|}{2bc} \quad \cdots [1], \\
\frac{\mathrm{BH}}{a} &= |\cos B| = \frac{|c^2+a^2-b^2|}{2ca} \quad \cdots [2], \\
\frac{\mathrm{CH}}{b} &= \sin A = \frac{2S}{bc} \quad \cdots [3]
\end{aligned}\]
が成り立つ.
- (2)
- $[1]$~$[3]$ から, \[\begin{aligned} 2c\cdot\mathrm{AH} &= |b^2+c^2-a^2|, \\ 2c\cdot\mathrm{BH} &= |c^2+a^2-b^2|, \\ c\cdot\mathrm{CH} &= 2S \end{aligned}\] が成り立つ. $a,$ $b,$ $c$ と $S$ が整数であるならば, これらの値は整数である.
参考
- 各辺の長さと面積が整数である三角形を「ヘロンの三角形」(Heronian triangle) と呼ぶ.
「ピタゴラスの三角形」(各辺の長さが整数である直角三角形) は「ヘロンの三角形」である.
よって, $1$ 組の辺の長さが等しい $2$ つの「ピタゴラスの三角形」の等辺を貼り合わせたり,
一方から他方を取り除いたりすることで,「ヘロンの三角形」が作れる.
例えば, $3$ 辺の長さが $9,$ $12,$ $15$ の三角形, $5,$ $12,$ $13$ の三角形において,
長さが $12$ の辺を貼り合わせると $3$ 辺の長さが $13,$ $14,$ $15$ の「ヘロンの三角形」が,
前者から後者を取り除くと $3$ 辺の長さが $4,$ $13,$ $15$ の「ヘロンの三角形」が得られる.
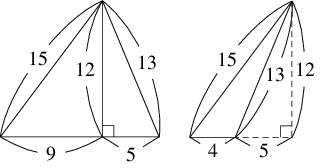
- 逆に, すべての「ヘロンの三角形」は $2$ つの「ピタゴラスの三角形」からこのようにして得られる三角形に相似であることが, 本問の結果からわかる.
- 「ヘロンの三角形」の $3$ 辺の長さの比は, $mn > h^2 \geqq \dfrac{m^2n}{2m+n},$ $m \geqq n$ なる互いに素な正の整数 $m,$ $n,$ $h$ を用いて \[ n(m^2+h^2):m(n^2+h^2):(m+n)(mn-h^2)\] と表されることが知られている.
問題《ヘロンの公式とブラーマグプタの三角形》
次のことを示せ.
- (1)
- $\triangle\mathrm{ABC}$ において, 周の半分の長さを $s$ とおく.
このとき,
\[\triangle\mathrm{ABC} = \sqrt{s(s-a)(s-b)(s-c)}\]
が成り立つ.
(参考: $2019$ 京都府立大, $2010$ 大阪教育大ほか)
- (2)
- $3$ 辺の長さが $b-1,$ $b,$ $b+1$ である三角形の面積 $S$ が整数であるとする. このとき, $b$ は偶数であり, $x = \dfrac{b}{2}$ とおくと, ある正の整数 $y$ に対して $x^2-3y^2 = 1$ となる.
解答例
- (1)
- 三角比の相互関係, 余弦定理により, \[\begin{aligned} &(\triangle\mathrm{ABC})^2 = \frac{1}{4}b^2c^2\sin ^2A \\ &= \frac{1}{4}b^2c^2(1-\cos ^2A) \\ &= \frac{1}{4}b^2c^2-\frac{1}{4}b^2c^2\cdot\frac{(b^2+c^2-a^2)^2}{4b^2c^2} \\ &= \frac{1}{16}\{ (2bc)^2-(b^2+c^2-a^2)^2\} \\ &= \frac{1}{16}(2bc+b^2+c^2-a^2)(2bc-b^2-c^2+a^2) \\ &= \frac{1}{16}\{ (b+c)^2-a^2\}\{ a^2-(b-c)^2\} \\ &= \frac{a+b+c}{2}\cdot\frac{b+c-a}{2}\cdot\frac{c+a-b}{2}\cdot\frac{a+b-c}{2} \\ &= s(s-a)(s-b)(s-c) \end{aligned}\] が成り立つ. よって, 両辺の正の平方根をとると, \[\triangle\mathrm{ABC} = \sqrt{s(s-a)(s-b)(s-c)}\] が得られる.
- (2)
- (1) により,
\[\begin{aligned}
S &= \sqrt{\frac{3b}{2}\left(\frac{3b}{2}-b+1\right)\left(\frac{3b}{2}-b\right)\left(\frac{3b}{2}-b-1\right)} \\
&= \frac{\sqrt{3b(b+2)b(b-2)}}{4} \\
&= \frac{b\sqrt{3(b^2-4)}}{4}
\end{aligned}\]
が成り立つ.
$b$ が奇数であるとすると, $b^2-4$ も奇数になり, 右辺の分子は奇数になってしまい, $S$ が整数であることに反する.
よって, $b$ は偶数である. そこで, $x = \dfrac{b}{2}$ とおくと, \[ S = \frac{2x\sqrt{3(4x^2-4)}}{4} = x\sqrt{3(x^2-1)}\] となる. これは整数であるから, ある正の整数 $y$ に対して $x^2-1 = 3y^2$ つまり $x^2-3y^2 = 1$ となる.
参考
- (1) で示した等式は「ヘロンの公式」(Heron's formula) と呼ばれる (別証明はこちらを参照).
- $3$ 辺の長さと面積が整数であるような三角形を「ヘロンの三角形」(Heronian triangle) と呼び, そのうち $3$ 辺の長さが連続する整数であるものを「ブラーマグプタの三角形」(Brahmagupta triangle) と呼ぶ. 本問の結果により,「ブラーマグプタの三角形」の $2$ 番目に長い辺の長さ $b$ と「ペル方程式」$x^2-3y^2 = 1$ の解は, $b = 2x$ により, もれも重複もなく対応する. 「ペル方程式」の解の公式により $x^2-3y^2 = 1$ のすべての正の整数解は \[ (x,y) \!\!=\!\! \left(\!\frac{(2\!+\!\sqrt 3)^n\!+\!(2\!-\!\sqrt 3)^n}{2},\frac{(2\!+\!\sqrt 3)^n\!-\!(2\!-\!\sqrt 3)^n}{2\sqrt 3}\!\right)\] と表されるから, $b$ は \[ b = (2+\sqrt 3)^n+(2-\sqrt 3)^n\] と表される.
- 四面体についても, $6$ 本の辺の長さから体積を求める公式が知られている.
問題《三角形のブロカール角の範囲》
$\triangle\mathrm{ABC}$ の内部の点 $\mathrm P$ が $\angle\mathrm{PAB} = \angle\mathrm{PBC} = \angle\mathrm{PCA} = \theta$ を満たすとし (点 $\mathrm P$ の存在と一意性についてはこちらを参照),
$S = \triangle\mathrm{ABC}$ とおく.
次のことを示せ.
- (1)
- \[\tan\theta = \frac{4S}{a^2+b^2+c^2}\] が成り立つ.
- (2)
- $\theta \leqq 30^\circ$ であり, 等号成立は $\triangle\mathrm{ABC}$ が正三角形の場合に限る. ただし, $s = \dfrac{a+b+c}{2}$ とおくとき,「ヘロンの公式」 \[ S = \sqrt{s(s-a)(s-b)(s-c)}\] (こちらを参照) が成り立つことは証明なしに使ってよい.
解答例
- (1)
- $a' = \mathrm{PA},$ $b' = \mathrm{PB},$ $c' = \mathrm{PC}$ とおく. $\triangle\mathrm{PAB}$ に余弦定理を適用すると, \[\begin{aligned} 4\triangle\mathrm{PAB} &= 2a'c\sin\theta = 2a'c\cos\theta\tan\theta \\ &= (a'^2+c^2-b'^2)\tan\theta \end{aligned}\] が得られる. 同様に, \[\begin{aligned} 4\triangle\mathrm{PBC} &= (b'^2+a^2-c'^2)\tan\theta, \\ 4\triangle\mathrm{PCA} &= (c'^2+b^2-a'^2)\tan\theta \end{aligned}\] が成り立つ. これらの辺々を加えると, \[\begin{aligned} 4S &= (a^2+b^2+c^2)\tan\theta \\ \tan\theta &= \frac{4S}{a^2+b^2+c^2} \end{aligned}\] が得られる.
- (2)
- (1) により \[\begin{aligned} &\theta \leqq 30^\circ \iff \tan\theta \leqq \frac{1}{\sqrt 3} \\ &\iff \tan ^2\theta \leqq \frac{1}{3} \iff \frac{16S^2}{(a^2+b^2+c^2)^2} \leqq \frac{1}{3} \\ &\iff (a^2+b^2+c^2)^2 \geqq 3\cdot 16S^2 \quad \cdots [1] \end{aligned}\] であるから, $[1]$ を示す. 「ヘロンの公式」により \[\begin{aligned} &(a^2+b^2+c^2)^2-3\cdot 16S^2 \\ &= (a^2+b^2+c^2)^2 \\ &\quad -3(a+b+c)(-a+b+c)(a-b+c)(a+b-c) \\ &= (a^2+b^2+c^2)^2 \\ &\quad +3(a+b+c)(a+b-c)(a-b+c)(a-b-c) \\ &= (a^2+b^2+c^2)^2+3\{ (a+b)^2-c^2\}\{ (a-b)^2-c^2\} \\ &= (a^2+b^2+c^2)^2 \\ &\quad +3[(a+b)^2(a-b)^2-\{ (a+b)^2+(a-b)^2\} c^2+c^4] \\ &= (a^2+b^2+c^2)^2 \\ &\quad +3\{ (a^2-b^2)^2-2(a^2+b^2)c^2+c^4\} \\ &= (a^4+b^4+c^4+2a^2b^2+2b^2c^2+2c^2a^2) \\ &\quad +3(a^4+b^4-2a^2b^2-2c^2a^2-2b^2c^2+c^4) \\ &= 2(2a^4+2b^4+2c^4-2a^2b^2-2b^2c^2-2c^2a^2) \\ &= 2\{ (a^2-b^2)^2+(b^2-c^2)^2+(c^2-a^2)^2\} \\ &\geqq 0 \end{aligned}\] が成り立つから, $[1]$ つまり $\theta \leqq 30^\circ$ が成り立つ. 等号成立は, $a = b = c$ つまり $\triangle\mathrm{ABC}$ が正三角形である場合に限る.
参考
$\triangle\mathrm{ABC}$ の内部にあり,
$\angle\mathrm{PAB} = \angle\mathrm{PBC} = \angle\mathrm{PCA} = \theta,$
$\angle\mathrm P'\mathrm{AC} = \angle\mathrm P'\mathrm{CB} = \angle\mathrm P'\mathrm{BA} = \theta$
を満たす点 $\mathrm P,$ $\mathrm P'$ をそれぞれ「第 $1$ ブロカール点」(first Brocard point),「第 $2$ ブロカール点」(second Brocard point),
$\theta$ を「ブロカール角」(Brocard angle) と呼ぶ.
問題《三角形の面積と外接円・内接円・傍接円》
$\triangle\mathrm{ABC}$ において, $S = \triangle\mathrm{ABC},$ $s = \dfrac{a+b+c}{2}$ とおく.
外接円の半径を $R,$ 内接円の半径を $r$ とおき, $\angle\mathrm A,$ $\angle\mathrm B,$ $\angle\mathrm C$ 内の傍接円 (こちらを参照) の半径をそれぞれ $r_{\mathrm A},$ $r_{\mathrm B},$ $r_{\mathrm C}$ とおく.
また, 頂点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ から対辺またはその延長に下ろした垂線の長さをそれぞれ $h_{\mathrm A},$ $h_{\mathrm B},$ $h_{\mathrm C}$ とおく.
このとき,
- (1)
- $S = \dfrac{abc}{4R}$
- (2)
- $S = rs$
- (3)
- $S = r_{\mathrm A}(s-a) = r_{\mathrm B}(s-b) = r_{\mathrm C}(s-c)$
- (4A)
- $S = \sqrt{rr_{\mathrm A}r_{\mathrm B}r_{\mathrm C}}$
- (4B)
- $r^{-1} = r_{\mathrm A}{}^{-1}+r_{\mathrm B}{}^{-1}+r_{\mathrm C}{}^{-1}$
- (4C)
- $r{}^{-1} = h_{\mathrm A}{}^{-1}+h_{\mathrm B}{}^{-1}+h_{\mathrm C}{}^{-1}$
- (4D)
- $4R+r = r_{\mathrm A}+r_{\mathrm B}+r_{\mathrm C}$
(参考: $2016$ 山口大)
解答例
- (1)
- 正弦定理により $\dfrac{a}{\sin A} = 2R$ であるから, \[ S = \frac{1}{2}bc\sin A = \frac{1}{2}bc\cdot\frac{a}{2R} = \frac{abc}{4R}\] が成り立つ.
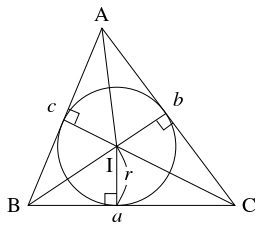
- (2)
- $\triangle\mathrm{ABC}$ の内心を $\mathrm I$ とおくと,
\[\begin{aligned}
S &= \triangle\mathrm{IBC}+\triangle\mathrm{ICA}+\triangle\mathrm{IAB} \\
&= \frac{1}{2}ra+\frac{1}{2}rb+\frac{1}{2}rc = \frac{1}{2}r(a+b+c) \\
&= rs
\end{aligned}\]
となる.
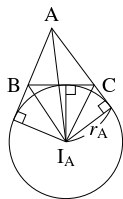
- (3)
- $\triangle\mathrm{ABC}$ の $\angle\mathrm A$ 内の傍心を $\mathrm I_{\mathrm A}$ とおくと,
\[\begin{aligned}
S &= \triangle\mathrm I_{\mathrm A}\mathrm{CA}+\triangle\mathrm I_{\mathrm A}\mathrm{AB}-\triangle\mathrm I_{\mathrm A}\mathrm{BC} \\
&= \frac{1}{2}r_{\mathrm A}b+\frac{1}{2}r_{\mathrm A}c-\frac{1}{2}r_{\mathrm A}a = \frac{1}{2}r_{\mathrm A}(b+c-a) \\
&= r_{\mathrm A}(s-a)
\end{aligned}\]
となる.
同様に, $S = r_{\mathrm B}(s-b) = r_{\mathrm C}(s-c)$ が成り立つ.
- (4A)
- $S^2 = s(s-a)(s-b)(s-c)$ に (2), (3) の結果
\[ S = rs, \quad s-a = \dfrac{S}{r_{\mathrm A}}, \quad s-b = \dfrac{S}{r_{\mathrm B}}, \quad s-c = \dfrac{S}{r_{\mathrm C}}\]
を代入すると ($S = rs$ は $S\cdot S$ の $1$ つに代入),
\[ S\cdot rs = s\cdot\dfrac{S}{r_{\mathrm A}}\cdot\dfrac{S}{r_{\mathrm B}}\cdot\dfrac{S}{r_{\mathrm C}}\]
から
$S^2 = rr_{\mathrm A}r_{\mathrm B}r_{\mathrm C}$ つまり $S = \sqrt{rr_{\mathrm A}r_{\mathrm B}r_{\mathrm C}}$が得られる.
- (4B)
- 順次 (3), (2) を使うと, \[\begin{aligned} &\dfrac{1}{r_{\mathrm A}}+\dfrac{1}{r_{\mathrm B}}+\dfrac{1}{r_{\mathrm C}} = \frac{s-a}{S}+\frac{s-b}{S}+\frac{s-c}{S} \\ &= \frac{3s-(a+b+c)}{S} = \frac{3s-2s}{S} = \frac{s}{S} = \frac{1}{r} \end{aligned}\] が得られる.
- (4C)
- 正弦定理により, \[ h_{\mathrm A} = c\sin B = \frac{bc}{2R}\] が成り立つ. 同様に, \[ h_{\mathrm B} = \frac{ca}{2R}, \quad h_{\mathrm C} = \frac{ab}{2R}\] が成り立つ. これらと (1), (2) により, \[\begin{aligned} &\frac{1}{h_{\mathrm A}}+\frac{1}{h_{\mathrm B}}+\frac{1}{h_{\mathrm C}} = \frac{2R}{bc}+\frac{2R}{ca}+\frac{2R}{ab} \\ &= \frac{2R(a+b+c)}{abc} = \frac{4Rs}{abc} = \frac{s}{S} = \frac{1}{r} \end{aligned}\] が得られる.
- (4D)
- 順次 (2), (3),「ヘロンの公式」, (1) を使うと, \[\begin{aligned} &r_{\mathrm A}+r_{\mathrm B}+r_{\mathrm C}-r \\ &= \frac{S}{s-a}+\frac{S}{s-b}+\frac{S}{s-c}-\frac{S}{s} \\ &= \frac{S^2}{S(s-a)}+\frac{S^2}{S(s-b)}+\frac{S^2}{S(s-c)}-\frac{S^2}{Ss} \\ &= \frac{s(s-b)(s-c)}{S}+\frac{s(s-c)(s-a)}{S} \\ &\qquad +\frac{s(s-a)(s-b)}{S}-\frac{(s-a)(s-b)(s-c)}{S} \\ &= \frac{s(s-c)(2s-a-b)}{S}+\frac{(s-a)(s-b)\{ s-(s-c)\}}{S} \\ &= \frac{s(s-c)c}{S}+\frac{(s-a)(s-b)c}{S} \\ &= \frac{\{ 2s^2-s(a+b+c)+ab\} c}{S} \\ &= \frac{(2s^2-s\cdot 2s+ab)c}{S} = \frac{abc}{S} = 4R \end{aligned}\] となるから, $r$ を移項すると求める等式が得られる.
参考
- (1) はヒッパルコスに知られていた. (4A) を「マシューの定理」(Mathieu's theorem), (4B) を「リュイリエの定理」(L'Huillier's theorem), (4C) を「テルケムの定理」(Terquem's theorem), (4D) を「フォイエルバッハの定理」(Feuerbach's theorem) と呼ぶ.
- (2), (3) から「ヘロンの公式」を, 次のように導くことができる.
$\triangle\mathrm{ABC}$ において, 内接円 $\mathrm I$ と辺 $\mathrm{BC}$ の接点を $\mathrm A'$, 傍接円 $\mathrm I_{\mathrm A}$ と辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の接点をそれぞれ $\mathrm A'',$ $\mathrm B_{\mathrm A},$ $\mathrm C_{\mathrm A}$ とおく.
このとき, $\mathrm{AB}_{\mathrm A} = \mathrm{AC}_{\mathrm A},$ $\mathrm{BA}'' = \mathrm{BC}_{\mathrm A},$ $\mathrm{CA}'' = \mathrm{CB}_{\mathrm A}$ から \[\begin{aligned} \mathrm{AB}_{\mathrm A}+\mathrm{AC}_{\mathrm A} &= \mathrm{AC}+\mathrm{CB}_{\mathrm A}+\mathrm{AB}+\mathrm{BC}_{\mathrm A} = b+\mathrm{CA}''+c+\mathrm{BA}'' \\ &= a+b+c = 2s \end{aligned}\] であるので,
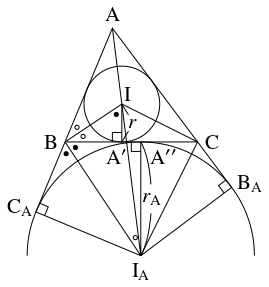
が成り立つ. さらに, $\mathrm{BI},$ $\mathrm{BI}_{\mathrm A}$ がそれぞれ $\angle\mathrm B$ の内角, 外角を二等分することから $\angle\mathrm A'\mathrm{BI},$ $\angle\mathrm A''\mathrm B\mathrm I_{\mathrm A}$ は互いに補角の関係にあるので, 直角三角形 $\mathrm A'\mathrm{BI},$ $\mathrm A''\mathrm I_{\mathrm A}\mathrm B$ は相似である. よって, \[\begin{aligned} \mathrm{IA}':\mathrm{BA}' &= \mathrm{BA}'':\mathrm I_{\mathrm A}\mathrm A'' \\ r:(s-b) &= (s-c):r_{\mathrm A} \\ rr_{\mathrm A} &= (s-b)(s-c) \end{aligned}\] が成り立つ ($\mathrm{BA}' = s-b$ はこちらを参照). よって, $S = rs,$ $S = r_{\mathrm A}(s-a)$ の辺々を掛け合わせて正の平方根をとると \[ S = \sqrt{rr_{\mathrm A}s(s-a)} = \sqrt{s(s-a)(s-b)(s-c)}\] が得られる.$\mathrm{AC}_{\mathrm A} = s$ よって $\mathrm{BA}'' = \mathrm{BC}_{\mathrm A} = \mathrm{AC}_{\mathrm A}-\mathrm{AB} = s-c$ - $3$ 辺の長さが $a,$ $b,$ $c$ である三角形の外接円の半径 $R$ と内接円の半径 $r$ の比は \[\frac{R}{r} = \frac{2abc}{(b+c-a)(c+a-b)(a+b-c)}\] であることが, (1), (2),「ヘロンの公式」によりわかる (参考: $2016$ 山口大).
問題《三角形の辺の長さと面積の不等式》
$\triangle\mathrm{ABC}$ において, $S = \triangle\mathrm{ABC}$ とおき, 外接円の半径を $R$ とおく.
$a \geqq b \geqq c$ つまり $A \geqq B \geqq C$ であるとする.
次のことを示せ.
- (1)
- $S = 2R^2\sin A\sin B\sin C$ が成り立つ.
- (2)
- $\sin A \geqq \sin B \geqq \sin C$ が成り立つ.
- (3)
- $S \leqq \dfrac{\sqrt 3}{4}a^2$ が成り立つ.
- (4)
- $\triangle\mathrm{ABC}$ が正三角形であるためには, $S = \dfrac{\sqrt 3}{4}a^2$ であることが必要十分である.
(参考: 茨城大, $2016$ 兵庫県立大)
解答例
- (1)
- 正弦定理により, \[\begin{aligned} S &= \frac{1}{2}ab\sin C = \frac{1}{2}\cdot 2R\sin A\cdot 2R\sin B\cdot\sin C \\ &= 2R^2\sin A\sin B\sin C \end{aligned}\] が成り立つ.
- (2)
- $a \geqq b \geqq c$ であるから, 正弦定理により \[ 2R\sin A \geqq 2R\sin B \geqq 2R\sin C\] つまり \[\sin A \geqq \sin B \geqq \sin C\] が成り立つ.
- (3)
- (1), (2), 正弦定理, および $A+B+C = 180^\circ,$ $A \geqq B \geqq C > 0^\circ$ から $0^\circ < C \leqq 60^\circ$ であることにより, \[\begin{aligned} \frac{S}{a^2} &= \frac{2R^2\sin A\sin B\sin C}{4R^2\sin ^2A} = \frac{\sin B\sin C}{2\sin A} \quad (\because (1)) \\ &\leqq \frac{\sin B\sin C}{2\sin B} = \frac{\sin C}{2} \quad (\because (2)) \\ &\leqq \frac{\sin 60^\circ}{2} = \frac{\sqrt 3}{4} \quad (\because 0^\circ < C \leqq 60^\circ ) \end{aligned}\] よって \[ S \leqq \frac{\sqrt 3}{4}a^2\] が成り立つ.
- (4)
- $\triangle\mathrm{ABC}$ が正三角形であるとき,
\[ S = \frac{1}{2}a^2\sin 60^\circ = \frac{\sqrt 3}{4}a^2\]
が成り立つ.
逆に, $S = \dfrac{\sqrt 3}{4}a^2$ が成り立つとすると, (3) の不等式で等号が成り立つことから, $\sin A = \sin B,$ $C = 60^\circ,$ よって $A = B = C = 60^\circ$ となり, $\triangle\mathrm{ABC}$ は正三角形となる.
以上から, $\triangle\mathrm{ABC}$ が正三角形であるためには, $S = \dfrac{\sqrt 3}{4}a^2$ であることが必要十分である.
参考
- $3$ 辺の長さが $a,$ $b,$ $c$ である三角形の面積 $S$ について「ヴァイツェンベックの不等式」(Weitzenböck's inequality) \[ S \leqq \frac{a^2+b^2+c^2}{4\sqrt 3}\] が成り立つ (証明はこちらを参照).
- 鋭角三角形の最大辺の長さが $a,$ 最小辺の長さが $c$ であるとき, 面積 $S$ について \[\frac{\sqrt 3}{4}c^2 \leqq S \leqq \frac{\sqrt 3}{4}a^2\] が成り立つ.
四角形の面積
問題《四角形の対角線と面積》
- (1)
- 長さが $p,$ $q,$ なす角が $\theta$ である対角線をもつ四角形の面積 $S$ は \[ S = \frac{1}{2}pq\sin\theta\] であることを示せ.
- (2)
- $k$ を正の数とする. 対角線の長さの和が $k$ である四角形のうち, 面積が最大であるものの面積を求めよ.
(参考: $2007$ 佐賀大)
解答例
- (1)
- 四角形 $\mathrm{ABCD}$ において, 対角線 $\mathrm{AC},$ $\mathrm{BD}$ の長さを $p,$ $q,$ なす角を $\theta,$ 交点を $\mathrm O$ とおき, 面積を $S$ とおく.
- (i)
- 四角形 $\mathrm{ABCD}$ が凸であるとき. $\sin (180^\circ -\theta ) = \sin\theta$ であるから, \[\begin{aligned} S &= \triangle\mathrm{OAB}+\triangle\mathrm{OBC}+\triangle\mathrm{OCD}+\triangle\mathrm{ODA} \\ &= \frac{1}{2}\mathrm{OA}\cdot\mathrm{OB}\sin\theta +\frac{1}{2}\mathrm{OB}\cdot\mathrm{OC}\sin\theta \\ &\qquad +\frac{1}{2}\mathrm{OC}\cdot\mathrm{OD}\sin\theta +\frac{1}{2}\mathrm{OD}\cdot\mathrm{OA}\sin\theta \\ &= \frac{1}{2}(\mathrm{OA}\cdot\mathrm{OB}\!+\!\mathrm{OB}\cdot\mathrm{OC}\!+\!\mathrm{OC}\cdot\mathrm{OD}\!+\!\mathrm{OD}\cdot\mathrm{OA})\sin\theta \\ &= \frac{1}{2}(\mathrm{OA}+\mathrm{OC})(\mathrm{OB}+\mathrm{OD})\sin\theta \\ &= \frac{1}{2}\mathrm{AC}\cdot\mathrm{BD}\sin\theta \\ &= \frac{1}{2}pq\sin\theta \end{aligned}\] が成り立つ.
- (ii)
- 四角形 $\mathrm{ABCD}$ が凸でないとき. $\angle\mathrm{BCD} > 180^\circ$ であるとしても一般性を失わないから, その場合を考える. $\sin (180^\circ -\theta ) = \sin\theta$ であるから, \[\begin{aligned} S &= \triangle\mathrm{OAB}-\triangle\mathrm{OBC}-\triangle\mathrm{OCD}+\triangle\mathrm{ODA} \\ &= \frac{1}{2}\mathrm{OA}\cdot\mathrm{OB}\sin\theta -\frac{1}{2}\mathrm{OB}\cdot\mathrm{OC}\sin\theta \\ &\qquad -\frac{1}{2}\mathrm{OC}\cdot\mathrm{OD}\sin\theta +\frac{1}{2}\mathrm{OD}\cdot\mathrm{OA}\sin\theta \\ &= \frac{1}{2}(\mathrm{OA}\cdot\mathrm{OB}\!-\!\mathrm{OB}\cdot\mathrm{OC}\!-\!\mathrm{OC}\cdot\mathrm{OD}\!+\!\mathrm{OD}\cdot\mathrm{OA})\sin\theta \\ &= \frac{1}{2}(\mathrm{OA}-\mathrm{OC})(\mathrm{OB}+\mathrm{OD})\sin\theta \\ &= \frac{1}{2}\mathrm{AC}\cdot\mathrm{BD}\sin\theta \\ &= \frac{1}{2}pq\sin\theta \end{aligned}\] が成り立つ.
- (2)
- 対角線の長さが $p,$ $q,$ なす角が $\theta,$ 面積が $S$ である四角形において, $p+q = k$ であるとする. このとき, (1) により \[\begin{aligned} S &= \frac{1}{2}pq\sin\theta \\ &= \frac{1}{2}p(k-p)\sin\theta \\ &= \frac{1}{2}(-p^2+kp)\sin\theta \\ &= \frac{1}{2}\left\{ -\left( p-\frac{k}{2}\right) ^2+\frac{k^2}{4}\right\}\sin\theta \end{aligned}\] であるから, $S$ は $p = \dfrac{k}{2},$ $\sin\theta = 1$ のとき, つまり $p = q = \dfrac{k}{2},$ $\theta = 90^\circ$ のとき最大値 $S = \dfrac{k^2}{8}$ をとる.
参考
(1) の公式は, ひし形,「たこ形」(長さの等しい隣り合う $2$ 辺の組 $2$ 組からなる四角形) の面積の公式 (対角線)$\,\times\,$(対角線)$\,\div 2$ の一般化になっている.
問題《四角形の対辺の長さの和の積と面積》
凸四角形 $\mathrm{ABCD}$ の面積 $S$ について
\[ S \leqq \frac{1}{4}(\mathrm{AB}+\mathrm{CD})(\mathrm{AD}+\mathrm{BC})\]
が成り立つことを示せ.
解答例
凸四角形 $\mathrm{ABCD}$ において, $a = \mathrm{AB},$ $b = \mathrm{BC},$ $c = \mathrm{CD},$ $d = \mathrm{DA},$ $A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C,$ $D = \angle\mathrm D$ とおく.
\[\begin{aligned}
S &= \triangle\mathrm{ABC}+\triangle\mathrm{ACD} = \frac{1}{2}ab\sin B+\frac{1}{2}cd\sin D \\
&\leqq \frac{1}{2}ab+\frac{1}{2}cd, \\
S &= \triangle\mathrm{ABD}+\triangle\mathrm{CBD} = \frac{1}{2}ad\sin A+\frac{1}{2}bc\sin C \\
&\leqq \frac{1}{2}ad+\frac{1}{2}bc
\end{aligned}\]
となるから, 辺々を加えて $2$ で割ると
\[ S \leqq \frac{1}{4}(ab+cd+ad+bc) = \frac{1}{4}(a+c)(b+d)\]
が得られる.
等号成立は, $\sin A = \sin B = \sin C = \sin D = 1,$ つまり $A = B = C = D = 90^\circ$ のときに限る.
よって,
\[ S \leqq \frac{1}{4}(\mathrm{AB}+\mathrm{CD})(\mathrm{AD}+\mathrm{BC})\]
が成り立ち, 等号成立は四角形 $\mathrm{ABCD}$ が長方形のときに限る.
問題《第二トレミーの定理》
円に内接する四角形 $\mathrm{ABCD}$ において,
\[\frac{\mathrm{DA}\cdot\mathrm{AB}+\mathrm{BC}\cdot\mathrm{CD}}{\mathrm{AB}\cdot\mathrm{BC}+\mathrm{CD}\cdot\mathrm{DA}} = \frac{\mathrm{AC}}{\mathrm{BD}}\]
が成り立つことを示せ.
ただし, $\triangle\mathrm{ABC}$ の外接円の半径が $R$ であるとき,
\[\triangle\mathrm{ABC} = \frac{\mathrm{BC}\cdot\mathrm{CA}\cdot\mathrm{AB}}{4R}\]
が成り立つこと (こちらを参照) は証明なしに使ってよい.
解答例
半径が $R$ の円に内接する四角形 $\mathrm{ABCD}$ の面積 $S$ は
\[\begin{aligned}
S &= \triangle\mathrm{ABC}+\triangle\mathrm{CDA} \\
&= \frac{\mathrm{BC}\cdot\mathrm{CA}\cdot\mathrm{AB}}{4R}+\frac{\mathrm{DA}\cdot\mathrm{AC}\cdot\mathrm{CD}}{4R} \\
&= \frac{\mathrm{AC}\cdot (\mathrm{AB}\cdot\mathrm{BC}+\mathrm{CD}\cdot\mathrm{DA})}{4R}, \\
S &= \triangle\mathrm{DAB}+\triangle\mathrm{BCD} \\
&= \frac{\mathrm{AB}\cdot\mathrm{BD}\cdot\mathrm{DA}}{4R}+\frac{\mathrm{CD}\cdot\mathrm{DB}\cdot\mathrm{BC}}{4R} \\
&= \frac{\mathrm{BD}\cdot (\mathrm{DA}\cdot\mathrm{AB}+\mathrm{BC}\cdot\mathrm{CD})}{4R}
\end{aligned}\]
と $2$ 通りに表されるので,
\[\mathrm{AC}\cdot (\mathrm{AB}\cdot\mathrm{BC}+\mathrm{CD}\cdot\mathrm{DA}) = \mathrm{BD}\cdot(\mathrm{DA}\cdot\mathrm{AB}+\mathrm{BC}\cdot\mathrm{CD})\]
から, 求める等式が得られる.
参考
- (2) の結果は「第二トレミーの定理」(second Ptolemy's theorem) と呼ばれる.
- 円に内接する四角形の対角線の長さの積に関する「第一トレミーの定理」(こちらを参照) と呼ばれる定理もある.
問題《ブラーマグプタの公式》
円に内接する四角形 $\mathrm{ABCD}$ において, $a = \mathrm{AB},$ $b = \mathrm{BC},$ $c = \mathrm{CD},$ $d = \mathrm{DA}$ とおき, 周の長さの半分を $s$ とおく.
このとき, 四角形 $\mathrm{ABCD}$ の面積 $S$ は
\[ S = \sqrt{(s-a)(s-b)(s-c)(s-d)}\]
と表されることを示せ.
(参考: $2021$ 山口大,$2019$ 京都府立大,$2017$ 大阪教育大ほか)
解答例
$\theta = \angle\mathrm{ABC}$ とおく.
$\angle\mathrm{CDA} = 180^\circ -\theta$ であるから,
\[\begin{aligned}
S &= \triangle\mathrm{ABC}+\triangle\mathrm{CDA} \\
&= \frac{1}{2}ab\sin \theta +\frac{1}{2}cd\sin (180^\circ -\theta ) \\
&= \frac{1}{2}(ab+cd)\sin\theta \\
&= \frac{1}{2}(ab+cd)\sqrt{1-\cos ^2\theta}
\end{aligned}\]
が成り立つ.
$\cos (180^\circ -\theta ) = -\cos\theta$ であるから, $\triangle\mathrm{ABC},$ $\triangle\mathrm{CDA}$ に余弦定理を適用すると
\[\mathrm{AC}^2 = a^2+b^2-2ab\cos\theta = c^2+d^2+2cd\cos\theta \]
となり,
\[\cos\theta = \frac{a^2+b^2-c^2-d^2}{2(ab+cd)}\]
となる.
よって,
\[\begin{aligned}
S^2 &= \frac{1}{4}(ab+cd)^2(1-\cos ^2\theta ) \\
&= \frac{1}{4}(ab+cd)^2-\frac{1}{4}(ab+cd)^2\cdot\frac{(a^2+b^2-c^2-d^2)^2}{4(ab+cd)^2}
\end{aligned}\]
\[\begin{aligned}
&= \frac{1}{16}\{ 4(ab+cd)^2-(a^2+b^2-c^2-d^2)^2\} \\
&= \frac{1}{16}\{ (2ab+2cd)^2-(a^2+b^2-c^2-d^2)^2\} \\
&= \frac{1}{16}(2ab+2cd-a^2-b^2+c^2+d^2) \\
&\qquad \cdot (2ab+2cd+a^2+b^2-c^2-d^2) \\
&= \frac{1}{16}\{ (c+d)^2-(a-b)^2\}\{ (a+b)^2-(c-d)^2\} \\
&= \frac{-a+b+c+d}{2}\cdot\frac{a-b+c+d}{2} \\
&\qquad \cdot\frac{a+b-c+d}{2}\cdot\frac{a+b+c-d}{2} \\
&= (s-a)(s-b)(s-c)(s-d)
\end{aligned}\]
が成り立つから, 両辺の正の平方根をとると
\[ S = \sqrt{(s-a)(s-b)(s-c)(s-d)}\]
が得られる.
参考
- 上記の公式は「ブラーマグプタの公式」(Brahmagupta's formula) として知られている. 便宜的に $d = 0$ とすると, 上述の「ヘロンの公式」が得られる.
- $n \geqq 5$ のとき, 円に内接する $n$ 角形の面積を辺の長さをもとに加減乗除または累乗根をとる操作の繰り返しで表す公式は存在しないことが, 近年, ヴァルフォロメーエフ, および松本幸夫氏らにより,「ガロア理論」を用いて独立に証明された. 例えば, $5$ 辺の長さが $1,$ $1,$ $2,$ $3,$ $4$ である五角形は円に内接するが, その面積は有理数から加減乗除または累乗根をとる操作の繰り返しで表せないことが知られている (参考文献: Y. Matsumoto, Y. Matsutani, M. Oka, T. Sakai and T. Shibuya, On the area of a polygon inscribed in a circle, L'Enseignement Mathématique (2) 53 (2007), 127–153).
- 「ブラーマグプタの公式」は, 一般の四角形の面積に関する「ブレートシュナイダーの公式」(Bretschneider's formula) \[ S = \sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos ^2\frac{\theta}{2}}\] ($\theta$: $1$ 組の向かい合う角の和) に一般化される (こちらを参照).
