作図不可能問題
作図可能性
ユークリッドが体系化したいわゆる初等幾何学は,
本稿では, この視点に立ち, $xy$ 平面において,
- 定規 (直線を引く機能のみをもつ, 目盛りが付いていても使わない)
- コンパス (円を描く機能のみをもつ)
本稿では, この視点に立ち, $xy$ 平面において,
原点 $\mathrm O(0,0),$ 点 $\mathrm E(1,0)$ を含む集合 $I$
が与えられているとして, 次の問題を考える.
問題《作図可能性》
どのような図形が $I$ から定規とコンパスのみを用いて作図できるか.
定規とコンパスによる作図可能性は, 次のように定式化できる.
定義《図形の作図可能性》
$I$ に属する $2$ 点 $\mathrm P,$ $\mathrm Q$ $(\mathrm P \neq \mathrm Q)$ に対して
点, 図形が $I$ から作図可能でないとき, $I$ から作図不可能 (unconstructible) であるという.
- (D1)
- 直線 $\mathrm{PQ},$ 線分 $\mathrm{PQ},$ 半直線 $\mathrm{PQ}$ を引く
- (D2)
- $\mathrm P$ を中心とし, $\mathrm Q$ を通る円周を描く
- (D3)
- $2$ 本の直線 $l,$ $m$ が交わるとき, 交点をとる
- (D4)
- 円周 $C,$ 直線 $l$ が交わるか接するとき, 交点または接点をとる
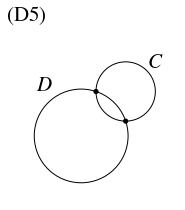
- (D5)
- 円周 $C,$ $D$ が交わるか接するとき, 交点または接点をとる
点, 図形が $I$ から作図可能でないとき, $I$ から作図不可能 (unconstructible) であるという.





まず, 直線 $\mathrm{OE}$ として $x$ 軸が引けて, $\mathrm O$ を通る $\mathrm{OE}$ の垂線として $y$ 軸が引ける.
点 $\mathrm P(a,b)$ から $x$ 軸, $y$ 軸に下ろした垂線の足が $\mathrm A(a,0),$ $\mathrm B(0,b)$ であるとき, $\{\mathrm O,\mathrm E,\mathrm P\}$ から $\mathrm A,$ $\mathrm B$ は作図可能であり, 逆に $\{\mathrm O,\mathrm E,\mathrm A,\mathrm B\}$ から $\mathrm P$ も作図可能である.
また, $x$ 軸上の点 $\mathrm A,$ $y$ 軸上の点 $\mathrm B$ が原点 $\mathrm O$ を中心とする同じ円周上にあるとき, $\{\mathrm O,\mathrm E,\mathrm A\}$ から $\mathrm B$ は作図可能であり, 逆に $\{\mathrm O,\mathrm E,\mathrm B\}$ から $\mathrm A$ も作図可能である.
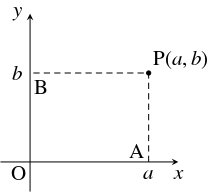
 このことを踏まえて, $I$ に属する点の $x$ 座標, $y$ 座標全体からなる集合を $I_0$ とおき, 作図可能性の定義を, 次のように言い換えておく.
このことを踏まえて, $I$ に属する点の $x$ 座標, $y$ 座標全体からなる集合を $I_0$ とおき, 作図可能性の定義を, 次のように言い換えておく.


定義《実数の作図可能性》
$x$ 軸上の点 $(\alpha,0)$ または $y$ 軸上の点 $(0,\alpha )$ が $I$ から作図可能であるとき, 実数 $\alpha$ は $I_0$ から作図可能であるという.
作図可能性について, 次の命題は基本的である.
命題《作図可能性》
- (1)
- 有理数体 $\mathbb Q$ に $I_0$ の元をすべて添加して得られる体 $\mathbb Q(I_0)$ の元は $I_0$ から作図可能である.
- (2)
- 正の数 $a$ が $I_0$ から作図可能であるとき, $\pm\sqrt a$ も $I_0$ から作図可能である.
証明
- (1)
- $0$ でない実数 $\alpha,$ $\beta$ が $I_0$ から作図可能であるとする.
\[\alpha +\beta,\ -\alpha,\ \alpha\beta,\ \frac{1}{\alpha}\]
が $I_0$ から作図可能であることを示せばよい.
- $x$ 軸上に点 $\mathrm A(\alpha,0)$ をとる.
点 $\mathrm A$ を中心とする半径 $|\beta |$ の円周と $x$ 軸の交点として点 $\mathrm C(\alpha +\beta,0)$ がとれるから(下図), $\alpha +\beta$ は $I_0$ から作図可能である.
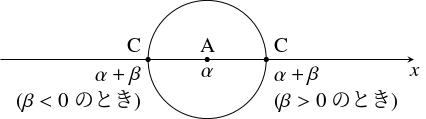
- $2$ 点 $\mathrm A(\alpha,0),$ $\mathrm A'(-\alpha,0)$ は原点 $\mathrm O$ を中心とする半径 $|\alpha |$ の円周上にあるから, $-\alpha$ も $I_0$ から作図可能である.
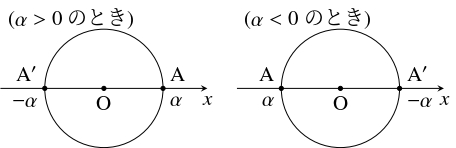
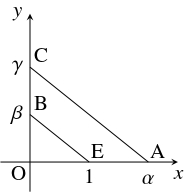
- $x$ 軸上に点 $\mathrm A(\alpha,0)$ をとり, $y$ 軸上に点 $\mathrm B(0,\beta )$ をとる.
さらに, 点 $\mathrm A$ を通って直線 $\mathrm{EB}$ に平行な直線と $y$ 軸の交点 $\mathrm C(0,\gamma )$ をとる.
このとき,
$1:\alpha = \beta :\gamma$ つまり $\gamma = \alpha\beta$となるから, $\alpha\beta$ は $I_0$ から作図可能である.
- $x$ 軸上に点 $\mathrm A(\alpha,0)$ をとり, $y$ 軸上に点 $\mathrm B(0,1)$ をとる.
さらに, 点 $\mathrm E$ を通って直線 $\mathrm{AB}$ に平行な直線と $y$ 軸の交点 $\mathrm C(0,\gamma )$ をとる.
このとき,
となるから, $\dfrac{1}{\alpha}$ は $I_0$ から作図可能である.$1:\alpha = \gamma :1, \quad \alpha\gamma = 1$ つまり $\gamma = \dfrac{1}{\alpha}$ 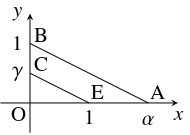
- $x$ 軸上に点 $\mathrm A(\alpha,0)$ をとる.
点 $\mathrm A$ を中心とする半径 $|\beta |$ の円周と $x$ 軸の交点として点 $\mathrm C(\alpha +\beta,0)$ がとれるから(下図), $\alpha +\beta$ は $I_0$ から作図可能である.
- (2)
- $x$ 軸上に点 $\mathrm B(1+a,0)$ をとり, 線分 $\mathrm{OB}$ の中点を中心とする半径 $\dfrac{1+a}{2}$ の円周を描く.
さらに, この円周と点 $\mathrm E$ を通る $x$ 軸の垂線の交点の $1$ つを $\mathrm C$ とおく.
$\triangle\mathrm{OEC},$ $\triangle\mathrm{CEB}$ は相似であり, $\alpha = \mathrm{EC}$ とおくと
となるから, $\sqrt a$ は $I_0$ から作図可能である.$1:\alpha = \alpha:a, \quad \alpha ^2 = a$ つまり $\alpha = \sqrt a$
例《作図可能性》
上記の命題の (1) により, すべての有理数, 特に $5$ は作図可能である.
よって, (2) により $\sqrt 5$ は作図可能であり, (1) により $\dfrac{1+\sqrt 5}{2}$ ($1$ 辺の長さが $1$ の正五角形の対角線の長さ) は作図可能である.
同様に, $\sqrt{\dfrac{5-\sqrt 5}{2}}$ (半径が $1$ の円に内接する正五角形の $1$ 辺の長さ) も作図可能である.
作図可能性は, 次のように判定できる.
定理《作図可能性の判定法》
実数 $\alpha$ に対して,
が成り立つ.
| $\alpha$ が $I_0$ から作図可能 |
| $\iff$ $K_0 \!=\! \mathbb Q(I_0),$ $[K_i\!:\!K_{i-1}] \!=\! 2$ $(1 \!\leqq\! i \!\leqq\! r),$ $\alpha \!\in\! K_r$ $\cdots [\ast ]$ |
| を満たす体の拡大の列 $\mathbb R \supset K_r \supset \cdots \supset K_1 \supset K_0$ が存在 |
証明
$K = \mathbb Q(I_0)$ とおく.
逆に, $[\ast ]$ を満たす体の拡大の列 $\mathbb R \supset K_r \supset \cdots \supset K_1 \supset K_0$ の存在を仮定する. $K_i$ $(1 \leqq i \leqq r)$ は $K_{i-1}$ に属する正の数 $d_{i-1}$ を用いて $K_i = K_{i-1}(\sqrt{d_{i-1}})$ と表され, その各元は $a_1+a_2\sqrt{d_{i-1}}$ $(a_1,a_2 \in K_{i-1})$ の形に表される. 上記の命題と数学的帰納法により, $K_i$ $(1 \leqq i \leqq r)$ の元は $I_0$ から作図可能であることがわかる. ゆえに, $\alpha$ は $I_0$ から作図可能である.
- (I)
- $I$ から作図可能な $2$ 本の直線の交点の $x$ 座標, $y$ 座標は $K$ 上の連立 $1$ 次方程式 \[ a_1x+b_1y = c_1, \quad a_2x+b_2y = c_2\] の解であるから, $K$ の元である.
- (II)
- $I$ から作図可能な円周と直線の共有点の $x$ 座標, $y$ 座標は $K$ 上の連立 $2$ 次方程式
\[ (x-p)^2+(y-q)^2 = r^2, \quad ax+by = c\]
の解である.
- (i)
- $b \neq 0$ のとき. 第 $2$ 式は $y = mx+n$ の形に変形できる. これを第 $1$ 式に代入すると $x$ の $2$ 次方程式が得られるから, 共有点の $x$ 座標は $K$ の $2$ 次拡大体または $K$ の元であり, $y = mx+n$ により $y$ 座標も同じ体の元である.
- (ii)
- $b = 0$ のとき. 第 $2$ 式は $y = n$ の形に変形できるから, 共有点の $y$ 座標は $K$ の元である. $y = n$ を第 $1$ 式に代入すると $x$ の $2$ 次方程式が得られるから, 共有点の $x$ 座標は $K$ の $2$ 次拡大体または $K$ の元である.
- (III)
- $I$ から作図可能な $2$ つの円周の共有点は, $2$ つの円周の交点を通る直線または共通接線 (根軸と呼ばれる) と $1$ つの円の共有点であるから, (II) によりその $x$ 座標, $y$ 座標は $K$ の $2$ 次拡大体または $K$ の元である.
逆に, $[\ast ]$ を満たす体の拡大の列 $\mathbb R \supset K_r \supset \cdots \supset K_1 \supset K_0$ の存在を仮定する. $K_i$ $(1 \leqq i \leqq r)$ は $K_{i-1}$ に属する正の数 $d_{i-1}$ を用いて $K_i = K_{i-1}(\sqrt{d_{i-1}})$ と表され, その各元は $a_1+a_2\sqrt{d_{i-1}}$ $(a_1,a_2 \in K_{i-1})$ の形に表される. 上記の命題と数学的帰納法により, $K_i$ $(1 \leqq i \leqq r)$ の元は $I_0$ から作図可能であることがわかる. ゆえに, $\alpha$ は $I_0$ から作図可能である.
ギリシアの作図不可能問題
次の問題は, 古代ギリシアで生まれ, 近代まで長らく未解決であったため, ギリシアの $3$ 大作図問題 (classical Greek construction problems) として広く知られている.
問題《ギリシアの $3$ 大作図問題》
- 円積問題 (Squaring the circle): 与えられた円の面積と同じ面積をもつ正方形の $1$ 辺の長さは作図可能であるか.
- 立方体倍積問題 (Doubling the cube): 与えられた立方体の $2$ 倍の体積をもつ立方体の $1$ 辺の長さは作図可能であるか.
- 角の三等分問題 (Angle trisection): 角の三等分線は作図可能であるか.
円積問題は, 円周率の超越性を示すことで, $19$ 世紀後半にリンデマンによって解決された (円周率の超越性は無理数論の問題であるから, ここではその証明を述べない).
例えば, 与えられた円の半径が $1$ であるとき, この円と同じ面積をもつ正方形の $1$ 辺の長さを $\alpha$ とおく.
このとき,
が成り立ち, $\pi$ の超越性により $\sqrt\pi$ は代数的でないから, $\alpha$ は作図不可能である.
以下では, $19$ 世紀前半にヴァンツェルによって解決された, 立方体倍積問題, 角の三等分問題について述べる.
| $\alpha ^2 = \pi$ つまり $\alpha = \sqrt\pi$ |
以下では, $19$ 世紀前半にヴァンツェルによって解決された, 立方体倍積問題, 角の三等分問題について述べる.
定理《立方体倍積問題》
立方体によっては, その $2$ 倍の体積をもつ立方体の $1$ 辺の長さは作図不可能である.
証明
与えられた立方体の $1$ 辺の長さが $a$ であるとき, この立方体の $2$ 倍の体積をもつ立方体の $1$ 辺の長さを $\alpha$ とおく.
このとき,
が成り立つから,
が成り立つ.
上記の定理により $\sqrt[3]{2}$ は作図不可能であるから, 例えば $a = 1$ のとき $\alpha$ は作図不可能である.
| $\alpha ^3 = 2a^3$ つまり $\alpha = \sqrt[3]{2}a$ |
| $\{ 0,1,a\}$ から $\alpha$ が作図可能 $\iff$ $\{ 0,1,a\}$ から $\sqrt[3]{2}$ が作図可能 |
例《立方体倍積問題》
上で示したように, $1$ 辺の長さが $1$ の立方体の $2$ 倍の体積をもつ立方体の $1$ 辺の長さは作図不可能である.
一方, $\{ 0,1,a\}$ から $a$ は作図可能であるから, $a = \sqrt[3]{2}$ のとき, $1$ 辺の長さが $a$ の立方体の $2$ 倍の体積をもつ立方体の $1$ 辺の長さは作図可能である.
一方, $\{ 0,1,a\}$ から $a$ は作図可能であるから, $a = \sqrt[3]{2}$ のとき, $1$ 辺の長さが $a$ の立方体の $2$ 倍の体積をもつ立方体の $1$ 辺の長さは作図可能である.
定理《角の三等分問題》
角によっては, その三等分線は作図不可能である.
証明
$\angle\mathrm{QPR}$ の三等分線について考える.
$\theta = \angle\mathrm{QPR},$ $a = \cos\theta,$ $\alpha = \cos\dfrac{\theta}{3}$ とおき, $x$ 軸と $\mathrm{PQ}$ のなす角を $\varphi$ とおく.
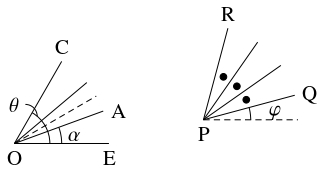 このとき, 頂点 $\mathrm P$ を原点 $\mathrm O$ に移す平行移動, $\mathrm O$ を中心とする角 $-\varphi$ の回転移動, 角の二等分線に関する対称移動を考えることにより,
このとき, 頂点 $\mathrm P$ を原点 $\mathrm O$ に移す平行移動, $\mathrm O$ を中心とする角 $-\varphi$ の回転移動, 角の二等分線に関する対称移動を考えることにより,
が成り立つ.
ここで, $3$ 倍角の公式により
\[\cos\theta = 4\cos ^3\frac{\theta}{3}-3\cos\frac{\theta}{3}\]
が成り立つから, $\alpha$ は $f(t) = 4t^3-3t-a$ の根である.
$f(t)$ は $\mathbb Q(c)$ 上可約であるとは限らない.
例えば, $\theta = 60^\circ$ のとき, $a = \dfrac{1}{2},$ $f(t) = 4t^3-3t-\dfrac{1}{2}$ であり, $f(t)$ は $\mathbb Q(c) = \mathbb Q$ 上既約である. 実際, 有理根定理により, $f(t) = 0$ の両辺を $2$ 倍して得られる整数係数方程式 \[ 8t^3-6t-1 = 0\] の有理数解の候補は \[ t = \pm 1,\ \pm\frac{1}{2},\ \pm\frac{1}{4},\ \pm\frac{1}{8}\] に限るが, 左辺にこれらの値を代入しても $0$ にならないから, $f(t) = 0$ は有理数解をもたない. $3$ 次多項式は可約であれば $1$ 次式で割り切れるから, このことは $f(t)$ が $\mathbb Q$ 上既約であることを意味する.
このように $f(t)$ が $\mathbb Q(c)$ 上既約であるとき, 上記の定理により, $\angle\mathrm{QPR}$ の三等分線は作図不可能である.

| $\angle\mathrm{QPR}$ の三等分線が作図可能 |
| $\iff$ $\angle\mathrm{EOC}$ の三等分線 $\mathrm{OA}$ で |
| $\angle\mathrm{EOA} = \dfrac{1}{3}\angle\mathrm{EOC}$ を満たすものが作図可能 |
| $\iff$ $\{ 0,1,a\}$ から $\alpha$ が作図可能 |
例えば, $\theta = 60^\circ$ のとき, $a = \dfrac{1}{2},$ $f(t) = 4t^3-3t-\dfrac{1}{2}$ であり, $f(t)$ は $\mathbb Q(c) = \mathbb Q$ 上既約である. 実際, 有理根定理により, $f(t) = 0$ の両辺を $2$ 倍して得られる整数係数方程式 \[ 8t^3-6t-1 = 0\] の有理数解の候補は \[ t = \pm 1,\ \pm\frac{1}{2},\ \pm\frac{1}{4},\ \pm\frac{1}{8}\] に限るが, 左辺にこれらの値を代入しても $0$ にならないから, $f(t) = 0$ は有理数解をもたない. $3$ 次多項式は可約であれば $1$ 次式で割り切れるから, このことは $f(t)$ が $\mathbb Q$ 上既約であることを意味する.
このように $f(t)$ が $\mathbb Q(c)$ 上既約であるとき, 上記の定理により, $\angle\mathrm{QPR}$ の三等分線は作図不可能である.
例《角の三等分問題》
上で示したように, $60^\circ$ の角の三等分線は作図不可能である.
一方, $90^\circ$ の角の三等分線は $60^\circ$ の角の二等分線であり, $60^\circ$ の角は作図可能であるから, $90^\circ$ の角の三等分線は作図可能である.
一方, $90^\circ$ の角の三等分線は $60^\circ$ の角の二等分線であり, $60^\circ$ の角は作図可能であるから, $90^\circ$ の角の三等分線は作図可能である.
高校数学の問題
複素数と方程式
問題《目盛付き定規が使える場合の立方体倍積問題》
$1$ 辺の長さが $1$ の正三角形 $\mathrm{ABC}$ において, 辺 $\mathrm{AB}$ の $\mathrm B$ を越える延長上に $\mathrm{BD} = 1$ なる点 $\mathrm D$ をとる.
また, 辺 $\mathrm{BC}$ の $\mathrm C$ を越える延長上の点 $\mathrm E$ を, $\mathrm{AE}$ と $\mathrm{CD}$ の交点 $\mathrm F$ について $\mathrm{EF} = 1$ となるようにとり, $x = \mathrm{AF}$ とおく.
さらに, 点 $\mathrm F$ を通って $\mathrm{AC}$ に平行な直線と $\mathrm{BE}$ の交点を $\mathrm G$ とおく.
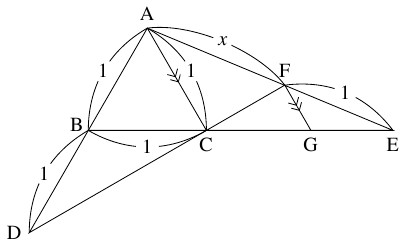

- (1)
- $x$ を用いて線分 $\mathrm{FG},$ $\mathrm{CF}$ の長さを表せ.
- (2)
- $x^4+2x^3-2x-4 = 0$ を示せ.
- (3)
- $x$ の値を求めよ.
解答例
こちらを参照.