高次方程式
高次方程式
定理《$n$ 次方程式の解の個数》
$n$ を正の整数とする.
複素数を係数とする $n$ 次の多項式 $f(x)$ に対して, 方程式 $f(x) = 0$ の相異なる解の個数は $n$ 以下である.
証明
$\alpha _1,$ $\cdots,$ $\alpha _r$ を $f(x) = 0$ の相異なる解とする.
因数定理により, $f(x)$ は $x-\alpha _1,$ $\cdots,$ $x-\alpha _r$ で割り切れる.
よって, $f(x)$ は $(x-\alpha _1)\cdots (x-\alpha _r)$ で割り切れ, $0$ でない多項式 $q(x)$ を用いて \[ f(x) = (x-\alpha _1)\cdots (x-\alpha _r)q(x)\] と書けるから, 両辺の次数を比較すると, \[ n = r+\deg q(x) \geqq r\] が得られる.
因数定理により, $f(x)$ は $x-\alpha _1,$ $\cdots,$ $x-\alpha _r$ で割り切れる.
よって, $f(x)$ は $(x-\alpha _1)\cdots (x-\alpha _r)$ で割り切れ, $0$ でない多項式 $q(x)$ を用いて \[ f(x) = (x-\alpha _1)\cdots (x-\alpha _r)q(x)\] と書けるから, 両辺の次数を比較すると, \[ n = r+\deg q(x) \geqq r\] が得られる.
累乗根は, 多くの教科書で指数関数の章で定義されるが, 高次方程式を解くうえで基本的な概念であるため (理論的には累乗根を使わずに解ける方程式は珍しい), この章で導入されることが望ましい.
定義《累乗根》
- (1)
- 正の整数 $n,$ 実数 $a$ に対して, $x^n = a$ の複素数解, つまり $n$ 乗すると $a$ になる複素数を $a$ の $n$ 乗根 ($n$-th root) と呼ぶ. $2$ 乗根, $3$ 乗根, $\cdots,$ をまとめて累乗根 (radical root) と呼ぶ.
- (2)
- 正の整数 $n,$ 正の数 $a$ に対して, $x^n = a$ を満たす正の数 $x$ がただ $1$ つ存在する. その正の数を $\sqrt[n]{a}$ で表す.
問題《累乗根の性質》
$m,$ $n$ を正の整数, $a,$ $b$ を正の数とする.
(A) $\sqrt[n]{a}\sqrt[n]{b} = \sqrt[n]{ab}$ (A)' $\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\dfrac{a}{b}}$ (A)'' $\sqrt[n]{a^nb} = a\sqrt[n]{b}$
(A) $\sqrt[n]{a}\sqrt[n]{b} = \sqrt[n]{ab}$ (A)' $\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\dfrac{a}{b}}$ (A)'' $\sqrt[n]{a^nb} = a\sqrt[n]{b}$
- (B)
- $(\sqrt[n]{a})^m = \sqrt[n]{a^m}$
- (C)
- $\sqrt[n]{\sqrt[m]{a}} = \sqrt[mn]{a}$
解答例
$\sqrt[n]{c}$ $(c > 0)$ は $x^n = c$ を満たすただ $1$ つの正の数であることを使う.
- (A)
- 指数法則により \[ (\sqrt[n]{a}\sqrt[n]{b})^n = (\sqrt[n]{a})^n(\sqrt[n]{b})^n = ab\] であるから, $\sqrt[n]{a}\sqrt[n]{b} = \sqrt[n]{ab}$ が成り立つ.
- (A)'
- 指数法則により \[\left(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\right) ^n = \frac{(\sqrt[n]{a})^n}{(\sqrt[n]{b})^n} = \frac{a}{b}\] であるから, $\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\dfrac{a}{b}}$ が成り立つ.
- (A)''
- (A) において $a$ を $a^n$ に置き換えると, \[\sqrt[n]{a^nb} = \sqrt[n]{a^n}\sqrt[n]{b} = a\sqrt[n]{b}\] が得られる.
- (B)
- 指数法則により \[\{ (\sqrt[n]{a})^m\} ^n = (\sqrt[n]{a})^{mn} = \{ (\sqrt[n]{a})^n\} ^m = a^m\] であるから, $(\sqrt[n]{a})^m = \sqrt[n]{a^m}$ が成り立つ.
- (C)
- 指数法則により \[ (\sqrt[n]{\sqrt[m]{a}})^{mn} = \{ (\sqrt[n]{\sqrt[m]{a}})^n\} ^m = (\sqrt[m]{a})^m = a\] であるから, $\sqrt[n]{\sqrt[m]{a}} = \sqrt[mn]{a}$ が成り立つ.
問題《有理根定理と累乗根の無理性》
$n$ を正の整数, $a$ を $n$ 乗数 (ある整数の $n$ 乗の形に表せる整数) でない正の整数とする.
- (1)
- $a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0 = 0$ ($a_k$: 整数, $a_0a_n \neq 0$) が有理数解 $\alpha$ をもつとする. $\alpha$ は $\alpha = \dfrac{p}{q}$ ($p$: $a_0$ の約数, $q$: $a_n$ の約数) の形に表されることを示せ.
- (2)
- (1) の結果を使って, $\sqrt[n]{a}$ は無理数であることを示せ.
解答例
- (1)
- $\alpha = \dfrac{p}{q}$ ($p,$ $q$: 互いに素な整数, $q > 0$) を与式の有理数解とする. このとき, \[\begin{aligned} a_n\alpha ^n+a_{n-1}\alpha ^{n-1}+\cdots +a_1\alpha +a_0 &= 0 \\ a_n\left(\frac{p}{q}\right) ^n\!+a_{n-1}\left(\frac{p}{q}\right) ^{n-1}\!+\cdots +a_1\left(\frac{p}{q}\right) +a_0 &= 0 \\ a_np^n+a_{n-1}p^{n-1}q+\cdots +a_1pq^{n-1}+a_0q^n &= 0 \end{aligned}\] が成り立つ. よって, \[ p(a_np^{n-1}+a_{n-1}p^{n-2}q+\cdots +a_1q^{n-1}) = -a_0q^n\] であるから, $p$ は $-a_0q^n$ を割り切る. $p,$ $q$ は互いに素であるから, $p$ は $a_0$ を割り切る. また, \[ q(a_{n-1}p^{n-1}+\cdots +a_1pq^{n-2}+a_0q^{n-1}) = -a_np^n\] であるから, $q$ は $-a_np^n$ を割り切る. $p,$ $q$ は互いに素であるから, $q$ は $a_n$ を割り切る. ゆえに, $\alpha$ は $\alpha = \dfrac{p}{q}$ ($p$: $a_0$ の約数, $q$: $a_n$ の約数) の形に表される.
- (2)
- $x^n-a = 0$ の有理数解があるとすれば, (1) の結果によりそれは $a$ の約数である.
しかし, $a$ の約数 $d$ に対して, $a$ が $n$ 乗数でないことから $a \neq d^n$ つまり $d^n-a \neq 0$ であるので, $d$ は $x^n-a = 0$ の解でない.
よって, $x^n-a = 0$ は有理数解をもたないから, $x^n-a = 0$ の解 $x = \sqrt[n]{a}$ は無理数である.
別解
- (2)
- $\sqrt[n]{a}$ が有理数であるとして, $a$ が $n$ 乗数であることを示す.
仮定により, $\sqrt[n]{a}$ は整数 $c,$ $d$ $(d \neq 0)$ を用いて
\[\sqrt[n]{a} = \frac{c}{d}\]
と表される.
両辺を $n$ 乗すると,
となる. 各素数 $p$ に対して, 整数 $x\,(\neq 0)$ の素因数分解における素数 $p$ の指数を $\mathrm{ord}_p(x)$ で表すとき, この関数は \[\mathrm{ord}_p(xy) = \mathrm{ord}_p(x)+\mathrm{ord}_p(y) \quad (xy \neq 0)\] を満たすから (素因数分解の一意性による), \[\mathrm{ord}_p(a)+n\,\mathrm{ord}_p(d) = n\,\mathrm{ord}_p(c)\] が成り立ち, $\mathrm{ord}_p(a) = n\,\mathrm{ord}_p(c)-n\,\mathrm{ord}_p(d)$ は $n$ の倍数である. ゆえに, $a$ の素因数分解における各素数の指数は $n$ の倍数であるから, $a$ は $n$ 乗数である. これで, 求める主張が示された.$a = \dfrac{c^n}{d^n}$ つまり $ad^n = c^n$
参考
- 多項式 $f(x)$ に対して, $f(x) = 0$ の解を $f(x)$ の「根」(root) と呼ぶ.
- (1) の結果は「有理根定理」(rational root theorem) として知られており, 因数分解, 因数定理を使って解くことができる整数係数の高次方程式の解を探すのに有用である.
問題《目盛付き定規が使える場合の立方体倍積問題》
$1$ 辺の長さが $1$ の正三角形 $\mathrm{ABC}$ において, 辺 $\mathrm{AB}$ の $\mathrm B$ を越える延長上に $\mathrm{BD} = 1$ なる点 $\mathrm D$ をとる.
また, 辺 $\mathrm{BC}$ の $\mathrm C$ を越える延長上の点 $\mathrm E$ を, $\mathrm{AE}$ と $\mathrm{CD}$ の交点 $\mathrm F$ について $\mathrm{EF} = 1$ となるようにとり, $x = \mathrm{AF}$ とおく.
さらに, 点 $\mathrm F$ を通って $\mathrm{AC}$ に平行な直線と $\mathrm{BE}$ の交点を $\mathrm G$ とおく.
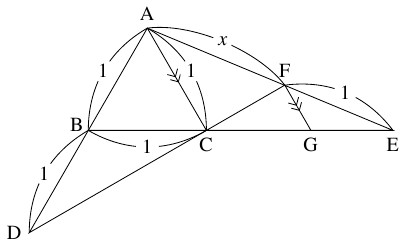

- (1)
- $x$ を用いて線分 $\mathrm{FG},$ $\mathrm{CF}$ の長さを表せ.
- (2)
- $x^4+2x^3-2x-4 = 0$ を示せ.
- (3)
- $x$ の値を求めよ.
解答例
- (1)
- $\triangle\mathrm{EFG}$ と $\triangle\mathrm{EAC}$ は相似であるから,
\[\begin{aligned}
\mathrm{EF}:\mathrm{FG} &= \mathrm{EA}:\mathrm{AC} \\
1:\mathrm{FG} &= (x+1):1 \\
\mathrm{FG} &= \frac{1}{x+1}
\end{aligned}\]
が得られる.
また, $\mathrm{BC} = \mathrm{BD} = 1$ から \[\angle\mathrm{BCD} = 60^\circ\div 2 = 30^\circ\] であり, \[\begin{aligned} \angle\mathrm{ACF} &= 180^\circ -\angle\mathrm{ACB}-\angle\mathrm{BCD} \\ &= 180^\circ -60^\circ -30^\circ = 90^\circ \end{aligned}\] である. よって, $\mathrm{AC}$ と $\mathrm{FG}$ が平行であることから \[\begin{aligned} \angle\mathrm{CFG} &= \angle\mathrm{ACF} = 90^\circ, \\ \angle\mathrm{FGC} &= \angle\mathrm{ACB} = 60^\circ \end{aligned}\] であるので, \[\mathrm{CF} = \sqrt 3\mathrm{FG} = \frac{\sqrt 3}{x+1}\] が得られる.
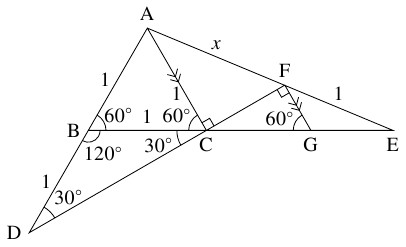
- (2)
- $\triangle\mathrm{ACF}$ において三平方の定理を適用すると, \[\begin{aligned} x^2 &= 1^2+\left(\frac{\sqrt 3}{x+1}\right) ^2 \\ x^2(x+1)^2 &= (x+1)^2+3 \\ x^2(x^2+2x+1) &= (x^2+2x+1)+3 \end{aligned}\] から \[ x^4+2x^3-2x-4 = 0\] となる.
- (3)
- 左辺を変形すると \[\begin{aligned} x^3(x+2)-2(x+2) &= 0 \\ (x^3-2)(x+2) &= 0 \end{aligned}\] となり, $x$ は正の数であるから $x = \sqrt[3]{2}$ である.
参考
ギリシアの三大作図問題として, 与えられた立方体の $2$ 倍の体積をもつ立方体の $1$ 辺の長さは作図可能であるか, つまり $\sqrt[3]{2}$ は定規とコンパスのみで作図できるか, という問題がある.
この問題は,「立方体倍積問題」(cube-doubling problem) または「デロスの問題」(Delian problem) などと呼ばれ, 長い間未解決であったが, $19$ 世紀に不可能であることが証明された (ピエール・ヴァンツェル, $1837$ 年).
しかし, 本問で見たように, $\sqrt[3]{2}$ は目盛付きの定規とコンパスを使えば作図できる ($\mathrm{EF} = 1$ を測るために定規の目盛を使う).
定理《実数係数方程式の共役な解》
実数係数方程式 $f(x) = 0$ が複素数 $\alpha$ を解にもつとき, $f(x) = 0$ は共役複素数 $\bar\alpha$ も解にもつ.
証明
こちらを参照.
問題《実数係数方程式の共役な解》
次のことを示せ.
- (1)
- 複素数 $\alpha,$ $\beta$ に対して, \[\overline{\alpha +\beta} = \bar\alpha +\bar\beta, \quad \overline{\alpha\beta} = \bar\alpha\bar\beta\] が成り立つ.
- (2)
- 実数係数方程式 $f(x) = 0$ が複素数 $\alpha$ を解にもつとき, $f(x) = 0$ は共役複素数 $\bar\alpha$ も解にもつ.
解答例
- (1)
- 複素数 $\alpha = a_1+a_2i,$ $\beta = b_1+b_2i$ ($a_1,$ $a_2,$ $b_1,$ $b_2$: 実数) に対して, \[\begin{aligned} \overline{\alpha +\beta} &= \overline{(a_1+a_2i)+(b_1+b_2i)} \\ &= \overline{(a_1+b_1)+(a_2+b_2)i} \\ &= (a_1+b_1)-(a_2+b_2)i \\ &= (a_1-a_2i)+(b_1-b_2i) \\ &= \bar\alpha +\bar\beta, \\ \overline{\alpha\beta} &= \overline{(a_1+a_2i)(b_1+b_2i)} \\ &= \overline{(a_1b_1-a_2b_2)+(a_1b_2+a_2b_1)i} \\ &= (a_1b_1-a_2b_2)-(a_1b_2+a_2b_1)i \\ &= (a_1-a_2i)(b_1-b_2i) \\ &= \bar\alpha\bar\beta \end{aligned}\] が成り立つ.
- (2)
- 実数係数多項式 $f(x) = a_nx^n+\cdots +a_1x+a_0$ について, $f(x) = 0$ が複素数 $\alpha$ を解にもつとする. このとき, $f(\alpha ) = 0$ の両辺の共役複素数をとると \[\begin{aligned} \overline{f(\alpha )} &= \bar 0 \\ \overline{a_n\alpha ^n+\cdots +a_1\alpha +a_0} &= 0 \\ \overline{a_n\alpha ^n}+\cdots +\overline{a_1\alpha}+\overline{a_0} &= 0 \\ \overline{a_n}\bar\alpha ^n+\cdots +\overline{a_1}\bar\alpha +\overline{a_0} &= 0 \\ a_n\bar\alpha ^n+\cdots +a_1\bar\alpha +a_0 &= 0 \\ f(\bar\alpha ) &= 0 \end{aligned}\] となるから, $f(x) = 0$ は $\bar\alpha$ も解にもつ.
参考
- 集合 $A$ の要素 $x$ に応じて集合 $A'$ の $1$ つの要素 $f(x)$ を対応させる規則を, $A$ から $A'$ への「写像」(map) と呼ぶ. 集合によっては, これを関数と呼ぶ.
- 四則演算が定義され, 結合法則, 交換法則, 分配法則を満たす, 少なくとも複数の要素をもつ集合を「体」(field) と呼ぶ. 有理数全体の集合 $\mathbb Q,$ 実数全体の集合 $\mathbb R,$ 複素数全体の集合 $\mathbb C$ は,「体」をなし, それぞれ「有理数体」,「実数体」,「複素数体」と呼ばれる.
- 「体」$K$ から「体」$K'$ への「写像」$\sigma$ で \[\sigma (a+b) = \sigma (a)+\sigma (b), \quad \sigma (ab) = \sigma (a)\sigma (b), \quad \sigma (1) = 1\] を満たすものを「体」の「準同型写像」(homomorphism) と呼ぶ. $\mathbb C$ から $\mathbb C$ への関数 $f(\alpha ) = \bar\alpha$ は「体」の「準同型写像」である. 「体」の「準同型写像」は, 方程式の理論, 特に「ガロア理論」で重要な役割を果たす.
問題《有理数係数方程式の共役な解》
$d$ を平方数でない整数とし, 有理数 $a_1,$ $a_2$ を用いて
\[\alpha = a_1+a_2\sqrt d \quad \cdots [1]\]
の形に表される複素数 $\alpha$ について, その全体の集合を $K$ とおき,
\[\sigma (\alpha ) = a_1-a_2\sqrt d\]
と定める ($K$ の要素は $[1]$ の形にただ $1$ 通りに表されることに注意, こちらを参照).
次のことを示せ.
- (1)
- 集合 $K$ の要素 $\alpha,$ $\beta$ に対して, \[\sigma (\alpha +\beta ) = \sigma (\alpha )+\sigma (\beta ), \quad \sigma (\alpha\beta ) = \sigma (\alpha )\sigma (\beta)\] が成り立つ.
- (2)
- 有理数係数方程式 $f(x) = 0$ が集合 $K$ の要素 $\alpha$ を解にもつとき, $f(x) = 0$ は $\sigma (\alpha )$ も解にもつ.
解答例
- (1)
- $K$ の要素 $\alpha = a_1+a_2\sqrt d,$ $\beta = b_1+b_2\sqrt d$ ($a_1,$ $a_2,$ $b_1,$ $b_2$: 有理数) に対して, \[\begin{aligned} \sigma (\alpha +\beta) &= \sigma ((a_1+a_2\sqrt d)+(b_1+b_2\sqrt d)) \\ &= \sigma ((a_1+b_1)+(a_2+b_2)\sqrt d) \\ &= (a_1+b_1)-(a_2+b_2)\sqrt d \\ &= (a_1-a_2\sqrt d)+(b_1-b_2\sqrt d) \\ &= \sigma (\alpha )+\sigma (\beta ), \\ \sigma (\alpha\beta ) &= \sigma ((a_1+a_2\sqrt d)(b_1+b_2\sqrt d)) \\ &= \sigma ((a_1b_1+da_2b_2)+(a_1b_2+a_2b_1)\sqrt d) \\ &= (a_1b_1+da_2b_2)-(a_1b_2+a_2b_1)\sqrt d \\ &= (a_1-a_2\sqrt d)(b_1-b_2\sqrt d) \\ &= \sigma (\alpha )\sigma (\beta ) \end{aligned}\] が成り立つ.
- (2)
- 有理数係数多項式 $f(x) = a_nx^n+\cdots +a_1x+a_0$ について, $f(x) = 0$ が $K$ の要素 $\alpha$ を解にもつとする. このとき, $f(\alpha ) = 0$ の両辺を $\sigma$ で送ると \[\begin{aligned} \sigma (f(\alpha )) &= \sigma (0) \\ \sigma (a_n\alpha ^n+\cdots +a_1\alpha +a_0) &= 0 \\ \sigma (a_n\alpha ^n)+\cdots +\sigma (a_1\alpha )+\sigma (a_0) &= 0 \\ \sigma (a_n)\sigma (\alpha )^n+\cdots +\sigma (a_1)\sigma (\alpha )+\sigma (a_0) &= 0 \\ a_n\sigma (\alpha )^n+\cdots +a_1\sigma (\alpha )+a_0 &= 0 \\ f(\sigma (\alpha )) &= 0 \end{aligned}\] となるから, $f(x) = 0$ は $\sigma (\alpha )$ も解にもつ.
参考
- 「体」$K$ (前問を参照) の要素を係数とする多項式を $K$ 上の多項式と呼ぶ. 定数でない「体」$K$ 上の多項式 $f(x)$ が定数と $f(x)$ の定数倍以外のすべての $K$ 上の多項式で割り切れないとき, $f(x)$ は $K$ 上「既約」(irreducible) であるという. また, 多項式 $f(x)$ について, $f(x) = 0$ の解を $f(x)$ の「根」(root) と呼ぶ.
- 本問において, $\alpha = a_1+a_2\sqrt d,$ $\sigma (\alpha ) = a_1-a_2\sqrt d$ は「有理数体」$\mathbb Q$ 上の同一の「既約多項式」$x^2-2a_1x+(a_1{}^2-da_2{}^2)$ の「根」である. 一般に, $\alpha,$ $\beta$ が「体」$K$ 上の同一の「既約多項式」の「根」であるとき, $\alpha,$ $\beta$ は互いに $K$ 上「共役」であるという. $K$ から $K$ への関数 $\sigma (\alpha )$ は「体」の「準同型写像」であり (前問を参照),「$2$ 次体」(こちらを参照) の理論において複素共役のような役割を果たす.
問題《$1$ の虚数立方根の性質と $3$ 次式の展開》
$\omega$ を $x^3 = 1$ の虚数解の $1$ つとする.
- (1)
- $\omega ^2+\omega +1$ の値を求めよ.
- (2)
- $a,$ $b$ を用いて $(a\omega +b\omega ^2)(a\omega ^2+b\omega )$ を表せ.
- (3)
- $(x+y+z)(x+\omega y+\omega ^2z)(x+\omega ^2y+\omega z)$ を簡単にせよ.
解答例
- (1)
- $\omega ^3 = 1$ であるから, $\omega ^3-1 = 0$ つまり \[ (\omega -1)(\omega ^2+\omega +1) = 0\] が成り立ち, $\omega \neq 1$ であるから, \[\omega ^2+\omega +1 = 0\] である.
- (2)
- (1) により, 与式は \[\begin{aligned} (a\omega +b\omega ^2)(a\omega ^2+b\omega ) &= (a^2+b^2)\omega ^3+ab(\omega ^2+\omega ^4) \\ &= (a^2+b^2)\cdot 1+ab (\omega ^2+\omega ) \\ &= a^2+b^2+ab\cdot (-1) \\ &= a^2-ab+b^2 \end{aligned}\] と表される.
- (3)
- (2) により \[\begin{aligned} &(x+\omega y+\omega ^2z)(x+\omega ^2y+\omega z) \\ &= x^2+(\omega y+\omega ^2z+\omega ^2y+\omega z)x+(\omega y+\omega ^2z)(\omega ^2y+\omega z) \\ &= x^2+(\omega +\omega ^2)(y+z)x+(y^2-yz+z^2) \\ &= x^2-(y+z)x+(y^2-yz+z^2) \\ \end{aligned}\] であるから, \[\begin{aligned} &(x+y+z)(x+\omega y+\omega ^2z)(x+\omega ^2y+\omega z) \\ &= (x+y+z)\{ x^2-(y+z)x+(y^2-yz+z^2)\} \\ &= x^3-(y+z)x^2+(y^2-yz+z^2)x \\ &\quad +(y+z)x^2-(y+z)^2x+(y+z)(y^2-yz+z^2) \\ &= x^3+(y^2-yz+z^2)x-(y^2+2yz+z^2)x+(y^3+z^3) \\ &= x^3+y^3+z^3-3xyz \end{aligned}\] である.
参考
等式
\[ x^3\!+\!y^3\!+\!z^3\!-\!3xyz = (x\!+\!y\!+\!z)(x\!+\!\omega y\!+\!\omega ^2z)(x\!+\!\omega ^2y\!+\!\omega z)\]
は $3$ 次方程式の「オイラーの解法」に利用される (こちらを参照).
$3$ 次方程式は, 解と係数の関係を利用して, $2$ 次方程式に帰着させて解くことができる.
問題《カルダーノによる $3$ 次方程式の解法》
$3$ 次方程式 $x^3-x-1 = 0\ \cdots [1]$ について, 次の問に答えよ.
- (1)
- $x = u+v$ であり, $u^3+v^3-1 = 3uv-1 = 0\ \cdots [2]$ であるならば, $[1]$ が成り立つことを示せ.
- (2)
- 複素数 $u,$ $v$ が $[2]$ を満たすとき, $u^3,$ $v^3$ を解にもつ $2$ 次方程式を $1$ つ作れ.
- (3)
- $1$ の虚数立方根 $\omega = \dfrac{-1+\sqrt 3i}{2}$ を用いて $[1]$ の解を表せ.
解答例
- (1)
- $x = u+v$ のとき, $u^3+v^3-1 = 3uv-1 = 0\ \cdots [2]$ ならば, \[\begin{aligned} x^3-x-1 &= (u+v)^3-(u+v)-1 \\ &= u^3+v^3+3uv(u+v)-(u+v)-1 \\ &= (u^3+v^3-1)+(3uv-1)(u+v) \\ &= 0+0\cdot (u+v) = 0 \quad \cdots [1] \end{aligned}\] が成り立つ.
- (2)
- 複素数 $u,$ $v$ が $[2]$ を満たすとする. このとき, \[ u^3+v^3 = 1, \quad u^3v^3 = (uv)^3 = \left(\frac{1}{3}\right) ^3 = \dfrac{1}{27}\] となるから, $2$ 次方程式の解と係数の関係により, $u^3,$ $v^3$ を解にもつ $2$ 次方程式 \[ t^2-t+\dfrac{1}{27} = 0 \quad \cdots [3]\] が得られる.
- (3)
- $[3]$ を解くと, $2$ 次方程式の解の公式により \[ t = \frac{1}{2}\left( 1\pm\sqrt{1-\frac{4}{27}}\right) = \frac{1}{2}\pm\frac{1}{6}\sqrt{\frac{23}{3}}\] となる. よって, $u^3 = \dfrac{1}{2}+\dfrac{1}{6}\sqrt{\dfrac{23}{3}},$ $v^3 = \dfrac{1}{2}-\dfrac{1}{6}\sqrt{\dfrac{23}{3}}$ とすると, \[\begin{aligned} u &= \sqrt[3]{\frac{1}{2}+\frac{1}{6}\sqrt{\frac{23}{3}}}\omega ^k \quad (k = 0,1,2), \\ v &= \sqrt[3]{\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}}\omega ^l \quad (l = 0,1,2) \end{aligned}\] となる. この $u,$ $v$ は $u^3+v^3-1 = 0$ を満たす. \[\begin{aligned} uv &= \sqrt[3]{\left(\frac{1}{2}+\frac{1}{6}\sqrt{\frac{23}{3}}\right)\left(\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}\right)}\omega ^{k+l} \\ &= \sqrt[3]{\frac{1}{4}-\frac{23}{4\cdot 27}}\omega ^{k+l} = \sqrt[3]{\frac{1}{27}}\omega ^{k+l} = \frac{1}{3}\omega ^{k+l} \end{aligned}\] から, $3uv-1 = 0$ となるのは $(k,l) = (0,0),$ $(1,2),$ $(2,1)$ の場合に限る. (1) で示したことから, これらの場合に $x = u+v$ は $[1]$ の解になる. $3$ 次方程式の解は $3$ つしかないから, $[1]$ の解は \[\begin{aligned} x = &\sqrt[3]{\frac{1}{2}+\frac{1}{6}\sqrt{\frac{23}{3}}}+\sqrt[3]{\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}}, \\ &\sqrt[3]{\frac{1}{2}+\frac{1}{6}\sqrt{\frac{23}{3}}}\omega +\sqrt[3]{\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}}\omega ^2, \\ &\sqrt[3]{\frac{1}{2}+\frac{1}{6}\sqrt{\frac{23}{3}}}\omega ^2+\sqrt[3]{\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}}\omega \end{aligned}\] と表される.
参考
- $2$ 次方程式に解の公式が存在するように, $3$ 次方程式, $4$ 次方程式にも解の公式が存在することが知られている. $3$ 次方程式 $x^3+a_2x^2+a_1x+a_0 = 0$ ($a_k$: 複素数) は, $x = X-\dfrac{a_2}{3}$ を代入して整理すると, $X^3+3pX+2q = 0$ ($p,$ $q$: 複素数) の形に変形できる. この方程式の解は, $\omega$ を $1$ の虚数立方根の $1$ つとすると, \[ X = \sqrt[3]{-q+\sqrt{q^2+p^3}}\omega ^k+\sqrt[3]{-q-\sqrt{q^2+p^3}}\omega ^{3-k}\ (k = 0,1,2)\] と表される. この公式を導く解法は, それを世に広めた『アルス・マグナ』の著者にちなんで「カルダーノの解法」(Cardano's method) と呼ばれることが多いが, 先に S・デル・フェッロと N・フォンタナ (タルタリア) によって発見された.
- $3$ 次方程式 $x^3 = x+1$ の実数解は「プラスチック数」(plastic number) と呼ばれ,
\[ P_1 = P_2 = 1,\ P_3 = 2, \quad P_{n+3} = P_n+P_{n+1}\]
で定義される「パドヴァン数列」(Padovan sequence) $\{ P_n\}$ の隣り合う $2$ 項の比の極限に等しい.
実際, 数列 $\left\{\dfrac{P_{n+1}}{P_n}\right\}$ が $x$ に収束する (証明は省略) とすると,
\[\frac{P_{n+3}}{P_{n+2}}\cdot\frac{P_{n+2}}{P_{n+1}}\cdot\frac{P_{n+1}}{P_n} = \frac{P_{n+3}}{P_n} = 1+\frac{P_{n+1}}{P_n}\]
から, $x^3 = 1+x$ となる.
なお,「フィボナッチ数列」が正方形をらせん状に並べたときの辺の長さから得られるのと同じように,「パドヴァン数列」は正三角形をらせん状に並べたときの辺の長さから得られる.
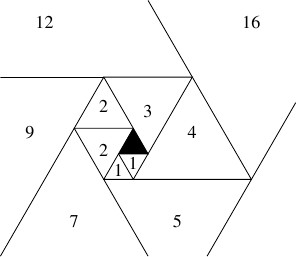
- 「プラスチック数」は \[ P_1 = 0,\ P_2 = 2,\ P_3 = 3, \quad P_{n+3} = P_n+P_{n+1}\] で定義される「ペラン数列」の隣り合う $2$ 項の比の極限に等しい.
- $1$ より大きい実数 $\alpha$ が, 最高次の係数が $1$ であって有理数の範囲でそれ以上因数分解できないような有理数係数方程式の解であり, 他の複素数解の絶対値が $1$ 未満であるとき, $\alpha$ を「ピゾ=ヴィジャヤラガヴァン数」(Pisot—Vijayaraghavan number) と呼ぶ. 「プラスチック数」は「ピゾ=ヴィジャヤラガヴァン数」の中で最小の数であることが知られている.
問題《複 $2$ 次方程式》
- (A)
- $x^4-5x^2+5 = 0$ を解け.
- (B)
- $80x^4-100x^2+1 = 0$ を解け.
解答例
- (A)
- 与式を変形すると \[\begin{aligned} x^4-2\cdot\frac{5}{2}x^2+\left(\frac{5}{2}\right) ^2 &= -5+\left(\frac{5}{2}\right) ^2 \\ \left( x^2-\frac{5}{2}\right) ^2 &= \frac{5}{4} \\ x^2-\frac{5}{2} &= \pm\frac{\sqrt 5}{2} \\ x^2 &= \frac{5\pm\sqrt 5}{2} \end{aligned}\] となるから, 求める解は \[ x = \pm\sqrt{\frac{5\pm\sqrt 5}{2}} = \pm\frac{\sqrt{10\pm 2\sqrt 5}}{2}\] である.
- (B)
- 与式を変形すると \[\begin{aligned} x^4-\frac{5}{4}x^2+\frac{1}{80} &= 0 \\ x^4-2\cdot\frac{5}{8}x^2+\left(\frac{5}{8}\right) ^2 &= -\frac{1}{80}+\left(\frac{5}{8}\right) ^2 \\ \left( x^2-\frac{5}{8}\right) ^2 &= \frac{121}{320} \\ x^2-\frac{5}{8} &= \pm\frac{11}{8\sqrt 5} \\ x^2 &= \frac{25\pm 11\sqrt 5}{40} \end{aligned}\] となるから, 求める解は \[ x = \pm\sqrt{\frac{25\pm 11\sqrt 5}{40}} = \pm\frac{1}{2}\sqrt{\frac{25\pm 11\sqrt 5}{10}}\] である.
参考
- $ax^4+bx^2+c$ ($a,$ $b,$ $c$: 定数, $a \neq 0$) の形の多項式を「複 $2$ 次式」(biquadratic polynomial) と呼ぶ.
- $1$ 辺の長さが $1$ である正二十面体の最長対角線は, 短辺の長さが $1,$ 長辺の長さが $\dfrac{1+\sqrt 5}{2}$ の長方形の対角線と一致するから, その長さ $x$ は, \[\begin{aligned} &x^2 = 1^2+\left(\frac{1+\sqrt 5}{2}\right) ^2 = \frac{5+\sqrt 5}{2} \\ &2x^2-5 = \sqrt 5 \\ &(2x^2-5)^2 = 5 \\ &4x^4-20x^2+20 = 0 \end{aligned}\] で, (A) の $4$ 次方程式の解である.
- (B) の $4$ 次方程式の解 $\dfrac{1}{2}\sqrt{\dfrac{25+11\sqrt 5}{10}}$ は, $1$ 辺の長さが $1$ である正十二面体の内接球の半径に等しい (こちらを参照).
問題《フェラーリによる $4$ 次方程式の解法》
$4$ 次方程式 $x^4+4x^3+16x^2+64x+256 = 0\ \cdots [*]$ について考える.
- (1)
- $[*]$ に $x = X-1$ を代入することにより, $4$ 次の項の係数が $1$ であって $3$ 次の項がない $X$ の $4$ 次方程式 $f(X) = 0$ を導け.
- (2)
- $f(X) = (X^2+t)^2-(pX+q)^2$ となるような $t,$ $p,$ $q$ の値を $1$ 組求めよ.
- (3)
- $[*]$ の解を求めよ.
解答例
- (1)
- $[*]$ に $x = X-1$ を代入すると, \[\begin{aligned} [*] &\iff x^4+4x^3+16x^2+64x+256 = 0 \\ &\iff (X-1)^4+4(X-1)^3 \\ &\qquad\qquad +16(X-1)^2+64(X-1)+256 = 0 \\ &\iff (X^4\!-\!4X^3\!+\!6X^2\!-\!4X\!+\!1)\!+\!4(X^3\!-\!3X^2\!+\!3X\!-\!1) \\ &\qquad\qquad +16(X^2-2X+1)+64(X-1)+256 = 0 \\ &\iff X^4+10X^2+40X+205 = 0 \quad \cdots [1] \end{aligned}\] となる.
- (2)
- \[\begin{aligned} &X^4+10X^2+40X+205 = (X^2+t)^2-(pX+q)^2 \\ &= X^4+(2t-p^2)X^2-2pqX+(t^2-q^2) \end{aligned}\] であるとき, $10 = 2t-p^2,$ $40 = -2pq,$ $205 = t^2-q^2$ が成り立つ. このとき, \[ p^2 = 2(t-5), \quad p^2q^2 = 400, \quad q^2 = t^2-205\] から \[\begin{aligned} 2(t-5)(t^2-205) &= 400 \\ t^3-5t^2-205t+825 &= 0 \end{aligned}\] であるので, $t = 15,$ $p = 2\sqrt 5,$ $q = -2\sqrt 5$ は条件を満たす.
- (3)
- $[1]$ は \[\begin{aligned} &(X^2+15)^2-(2\sqrt 5X-2\sqrt 5)^2 = 0 \\ &(X^2-2\sqrt 5X+15+2\sqrt 5)(X^2+2\sqrt 5X+15-2\sqrt 5) = 0 \end{aligned}\] と同値であるから, その解は \[\begin{aligned} X = \sqrt 5\pm\sqrt{10+2\sqrt 5}i,\ -\sqrt 5\pm\sqrt{10-2\sqrt 5}i \end{aligned}\] である. よって, $x = X-1$ から, $[*]$ の解は \[\begin{aligned} x = &-1+\sqrt 5\pm\sqrt{10+2\sqrt 5}i, \\ &-1-\sqrt 5\pm\sqrt{10-2\sqrt 5}i \end{aligned}\] の $4$ 個である.
参考
- $4$ 次方程式 $x^4+a_3x^3+a_2x^2+a_1x+a_0 = 0$ ($a_k$: 定数) は, 次の「フェラーリの解法」(Ferrari's method) と呼ばれる方法で解ける: 与式に $x = X-\dfrac{a_3}{4}$ を代入して $3$ 次の項がない形 $X^4+A_2X^2+A_1X+A_0 = 0$ ($A_k$: 複素数) に変形し, $A_1 \neq 0$ のときは, これをさらに $(X\text{ の }2\text{ 次式})^2-(X\text{ の}1\text{ 次式})^2 = 0$ の形に変形して解く (一般に, この形を導く際には $3$ 次方程式を解かなければならない).
- 本問では, $z^5 = 1$ の虚数解 \[\cos\left(\pm\dfrac{2\pi}{5}\right) +i\sin\left(\pm\dfrac{2\pi}{5}\right),\ \cos\left(\pm\dfrac{4\pi}{5}\right) +i\sin\left(\pm\dfrac{4\pi}{5}\right)\] の $4$ 倍, つまり $x^5 = 2^{10}$ の虚数解を求めた.
- $z^5 = 1$ の虚数解は「相反方程式」$z^4+z^3+z^2+z+1 = 0$ の解であり, $t = z+\dfrac{1}{z}$ という置き換えにより $2$ 次方程式に帰着させて解くことができる (こちらを参照).
