ベクトル方程式
平面図形のベクトル方程式
定理《平面における直線の方程式》
- (1)
- 点 $\mathrm P_0(\vec p_0)$ を通り, $\vec d$ に平行な直線 $l$ 上の点 $\mathrm P(\vec p)$ に対して,
が成り立つ.
$\vec p = \overrightarrow{p_0}+t\vec d$ ($t$: 実数) - (2)
- 点 $\mathrm P_0(x_0,y_0)$ を通り, $\vec d = (a,b)$ $(ab \neq 0)$ に平行な直線 $l$ の方程式は \[\frac{x-x_0}{a} = \frac{y-y_0}{b}\] である.
証明
- (1)
- $\overrightarrow{\mathrm P_0\mathrm P}$ は $\vec 0$ に等しいか $\vec d$ に平行であるから, $\overrightarrow{\mathrm P_0\mathrm P} = t\vec d$ を満たす実数 $t$ が存在して, \[\vec p = \overrightarrow{\mathrm{OP}} = \overrightarrow{\mathrm{OP}_0}+\overrightarrow{\mathrm P_0\mathrm P} = \overrightarrow{p_0}+t\vec d\] となる.
- (2)
- $l$ のベクトル方程式は
であるので, \[ x = x_0+ta, \quad y = y_0+tb\] から $t$ を消去すると, 求める方程式が得られる.
$(x,y) = (x_0,y_0)+t(a,b)$ ($t$: 実数)
定理《円周の方程式》
点 $\mathrm C$ を中心, $r$ を半径とする円周の方程式は
\[ |\overrightarrow{\mathrm{CP}}| = r\]
である.
証明
明らかである.
問題《ベクトルによる点と直線の距離の公式の証明》
$a,$ $b$ を $(a,b) \neq (0,0)$ なる実数とする.
点 $\mathrm P_0(x_0,y_0)$ と直線 $l:ax+by+c = 0$ の距離は
\[\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\]
であることを, ベクトルを用いて示せ.
解答例
点 $\mathrm P_0(x_0,y_0)$ から直線 $l:ax+by+c = 0$ に下ろした垂線の足を $\mathrm H(p,q)$ とおく.
$\overrightarrow{\mathrm P_0\mathrm H}$ は $l$ の法線ベクトル $\vec n = (a,b)$ に平行であるから,
ある実数 $k$ に対して
\[\overrightarrow{\mathrm P_0\mathrm H} = k\vec n\]
となる.
両辺の $\vec n$ との内積をとると
\[\vec n\cdot\overrightarrow{\mathrm P_0\mathrm H} = k|\vec n|^2\]
となるから,
\[\begin{aligned}
k &= \frac{\vec n\cdot\overrightarrow{\mathrm P_0\mathrm H}}{|\vec n|^2} \\
&= \frac{a(p-x_0)+b(q-y_0)}{a^2+b^2} \\
&= -\frac{ax_0+by_0-(ap+bq)}{a^2+b^2} \\
&= -\frac{ax_0+by_0+c}{a^2+b^2}
\end{aligned}\]
が成り立つ.
よって, 点 $\mathrm P_0$ と直線 $l$ の距離は
\[\begin{aligned}
|\overrightarrow{\mathrm P_0\mathrm H}| &= |k\vec n| = |k||\vec n| \\
&= \frac{|ax_0+by_0+c|}{a^2+b^2}\cdot\sqrt{a^2+b^2} \\
&= \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}
\end{aligned}\]
である.
参考
一般に, 座標平面上の相異なる $2$ 点 $\mathrm O,$ $\mathrm H$ に対して, $\mathrm H$ を通り, $\mathrm{OH}$ に垂直な直線は, ベクトル方程式
で表される.
$\overrightarrow{\mathrm{OH}} = h(\cos\theta,\sin\theta )$ とおくと, これは
\[ x\cos\theta +y\sin\theta = h\]
と表される.
これらの形の直線の方程式を「ヘッセ標準形」と呼ぶ (こちらも参照).
| $\overrightarrow{\mathrm{OH}}\cdot\overrightarrow{\mathrm{HP}} = 0$ つまり $\overrightarrow{\mathrm{OH}}\cdot\overrightarrow{\mathrm{OP}} = |\overrightarrow{\mathrm{OH}}|^2$ |
問題《円周の接線の方程式》
原点 $\mathrm O$ を中心とする半径 $r$ の円周 $x^2+y^2 = r^2$ に点 $\mathrm P_0(x_0,y_0)$ で接する直線を $l$ とおく.
点 $\mathrm P(x,y)$ に対して
\[\mathrm P \in l \iff x_0x+y_0y = r^2\]
が成り立つことを示せ.
解答例
点 $\mathrm P(x,y)$ に対して,
\[\begin{aligned}
\mathrm P \in l &\iff \mathrm P = \mathrm P_0\text{ または }\overrightarrow{\mathrm{OP}_0} \perp \overrightarrow{\mathrm P_0\mathrm P} \\
&\iff \overrightarrow{\mathrm{OP}_0}\cdot\overrightarrow{\mathrm P_0\mathrm P} = 0 \\
&\iff (x_0,y_0)\cdot (x-x_0,y-y_0) = 0 \\
&\iff x_0x+y_0y = x_0{}^2+y_0{}^2 \\
&\iff x_0x+y_0y = r^2
\end{aligned}\]
が成り立つ.
問題《方べきの定理》
定点 $\mathrm O$ を通る直線 $l$ と点 $\mathrm C$ を中心とする半径 $r$ の円周の $2$ つの共有点を $\mathrm P,$ $\mathrm Q$ とおく ($l$ と円周 $\mathrm C$ が接するときは, $\mathrm P = \mathrm Q$ と考える).
$\vec c = \overrightarrow{\mathrm{OC}}$ とおき, $l$ に平行な単位ベクトル $\vec e$ をとって, $\overrightarrow{\mathrm{OP}} = p\vec e,$ $\overrightarrow{\mathrm{OQ}} = q\vec e$ ($p,$ $q$: 実数) とおく.
- (1)
- $p,$ $q$ を解にもつ $2$ 次方程式の $1$ つを, $r,$ $|\vec c|,$ $\vec c\cdot\vec e$ を使って表せ.
- (2)
- $|\overrightarrow{\mathrm{OP}}||\overrightarrow{\mathrm{OQ}}|$ の値は直線 $l$ の向きによらず一定であることを示せ.
解答例
- (1)
- $|\overrightarrow{\mathrm{CP}}| = r$ から, \[\begin{aligned} &|\overrightarrow{\mathrm{CP}}|^2 = r^2 \\ &|p\vec e-\vec c|^2 = r^2 \\ &p^2|\vec e|^2-2p\vec c\cdot\vec e+|\vec c|^2 = r^2 \\ &p^2-2p\vec c\cdot\vec e+|\vec c|^2-r^2 = 0 \end{aligned}\] が成り立つ. 同様に, $q^2-2q\vec c\cdot\vec e+|\vec c|^2-r^2 = 0$ が成り立つ. ゆえに, $p,$ $q$ を解にもつ $2$ 次方程式の $1$ つは \[ t^2-2t\vec c\cdot\vec e+|\vec c|^2-r^2 = 0\] である.
- (2)
- 解と係数の関係により \[ |\overrightarrow{\mathrm{OP}}||\overrightarrow{\mathrm{OQ}}| = |p\vec e||q\vec e| = |pq||\vec e|^2 = |pq| = ||\vec c|^2-r^2|\] が成り立ち, この値は $l$ の向きによらず一定である.
参考
ベクトルの利用で, 次の方べきの定理の $3$ つの場合を同時に証明できた.
「解析幾何学」的な証明もある (こちらを参照).
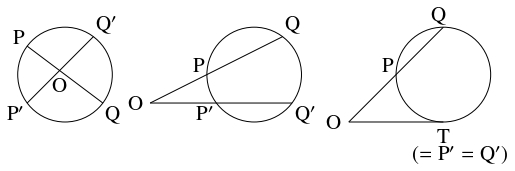
- (i)
- 円周の $2$ 本の弦 $\mathrm{PQ},$ $\mathrm P'\mathrm Q'$ が円の内部の点 $\mathrm O$ で交わるとき, $\mathrm{OP}\cdot\mathrm{OQ} = \mathrm{OP}'\cdot\mathrm{OQ}'$ が成り立つ.
- (ii)
- 円周の $2$ 本の弦 $\mathrm{PQ},$ $\mathrm P'\mathrm Q'$ の延長が円の外部の点 $\mathrm O$ で交わるとき, $\mathrm{OP}\cdot\mathrm{OQ} = \mathrm{OP}'\cdot\mathrm{OQ}'$ が成り立つ.
- (iii)
- 円の外部の点 $\mathrm O$ を通る直線が円周と $2$ 点 $\mathrm P,$ $\mathrm Q$ で交わり, 点 $\mathrm O$ から円周に引いた接線が点 $\mathrm T$ で接するとき, $\mathrm{OP}\cdot\mathrm{OQ} = \mathrm{OT}^2$ が成り立つ.
空間図形のベクトル方程式
定理《空間における直線の方程式》
- (1)
- 点 $\mathrm P_0(\vec p_0)$ を通り, $\vec d$ に平行な直線 $l$ 上の点 $\mathrm P(\vec p)$ に対して,
が成り立つ.
$\vec p = \overrightarrow{p_0}+t\vec d$ ($t$: 実数) - (2)
- 点 $\mathrm P_0(x_0,y_0,z_0)$ を通り, $\vec d = (a,b,c)$ $(abc \neq 0)$ に平行な直線 $l$ の方程式は \[\frac{x-x_0}{a} = \frac{y-y_0}{b} = \frac{z-z_0}{c}\] である.
証明
- (1)
- 平面上の直線と同様である.
- (2)
- $l$ のベクトル方程式は
であるので, \[ x = x_0+ta, \quad y = y_0+tb, \quad z = z_0+tc\] から $t$ を消去すると, 求める方程式が得られる.
$(x,y,z) = (x_0,y_0,z_0)+t(a,b,c)$ ($t$: 実数)
定理《平面の方程式》
点 $\mathrm A(x_0,y_0,z_0)$ を通り, $\vec 0$ でないベクトル $\vec n = (a,b,c)$ に垂直な平面 $\alpha$ と点 $\mathrm P(x,y,z)$ に対して,
\[\begin{aligned}
\mathrm P \in \alpha &\iff \vec n\cdot\overrightarrow{\mathrm{AP}} = 0 \\
&\iff \vec n\cdot (\overrightarrow{\mathrm{OP}}-\overrightarrow{\mathrm{OA}}) = 0 \\
&\iff a(x-x_0)+b(y-y_0)+c(z-z_0) = 0
\end{aligned}\]
が成り立つ.
定理《球面の方程式》
- (1)
- 点 $\mathrm C$ を中心, $r$ を半径とする球面の方程式は \[ |\overrightarrow{\mathrm{CP}}| = r\] である.
- (2)
- 点 $(a,b,c)$ を中心, $r$ を半径とする球面の方程式は \[ (x-a)^2+(y-b)^2+(z-c)^2 = r^2\] である.
証明
明らかである.
問題《ねじれの位置にある $2$ 直線に直交する直線》
空間内の $2$ 直線 $l,$ $m$ がねじれの位置にあるとする.
このとき, $l,$ $m$ に直交する直線がただ $1$ つ存在することを示せ.
(参考: $2024$ 大阪大)
解答例
$l$ が $y$ 軸と重なり, $m$ と $xy$ 平面が平行であるように座標軸を定める.
このとき, $l,$ $m$ は実数 $a,$ $b,$ $c$ $(c \neq 0)$ を用いてそれぞれ
\[ x = z = 0, \quad y-ax-b = z-c = 0\]
で表され, $l$ の方向ベクトルは $\vec d = (0,1,0),$ $m$ の方向ベクトルは $\vec e = (1,a,0)$ である.
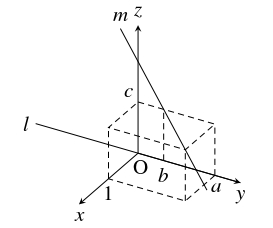$l$ 上の点 $\mathrm P(0,s,0),$ $m$ 上の点 $\mathrm Q(t,at+b,c)$ ($s,$ $t$: 実数) に対して,
\[\overrightarrow{\mathrm{PQ}} = (t,at+b-s,c)\]
であるから,
\[\begin{aligned}
&l \perp \mathrm{PQ},\ m \perp \mathrm{PQ} \\
&\iff \vec d\cdot\overrightarrow{\mathrm{PQ}} = 0,\ \vec e\cdot\overrightarrow{\mathrm{PQ}} = 0 \\
&\iff at+b-s = 0,\ t+a(at+b-s) = 0 \\
&\iff s = b,\ t = 0
\end{aligned}\]
が成り立つ.
ゆえに, $l,$ $m$ に直交する直線がただ $1$ つ存在する.
参考
空間内の $2$ 直線の距離には, ベクトルの「外積」,「行列式」を用いた公式がある.
問題《点と平面の距離とデカルト=グアの定理》
$\mathrm O$ を原点とする座標空間において, 次のことを示せ.
- (1)
- $a,$ $b,$ $c$ を $(a,b,c) \neq (0,0,0)$ なる実数とする. このとき, 点 $\mathrm P_0(x_0,y_0,z_0)$ と平面 $\alpha :ax+by+cz+d = 0$ の距離は \[\frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}\] である.
- (2)
- $\mathrm A(a,0,0),$ $\mathrm B(0,b,0),$ $\mathrm C(0,0,c)$ ($a,$ $b,$ $c$: 正の数) とする. このとき, \[ (\triangle\mathrm{ABC})^2 = (\triangle\mathrm{OBC})^2+(\triangle\mathrm{OCA})^2+(\triangle\mathrm{OAB})^2\] が成り立つ.
(参考: $1995$ 山形大)
解答例
- (1)
- 点 $\mathrm P_0(x_0,y_0,z_0)$ から平面 $\alpha :ax+by+cz+d = 0$ に下ろした垂線の足を $\mathrm H(p,q,r)$ とおく. $\overrightarrow{\mathrm P_0\mathrm H}$ は $\alpha$ の法線ベクトル $\vec n = (a,b,c)$ に平行であるから, ある実数 $k$ に対して \[\overrightarrow{\mathrm P_0\mathrm H} = k\vec n\] となる. 両辺の $\vec n$ との内積をとると \[\vec n\cdot\overrightarrow{\mathrm P_0\mathrm H} = k|\vec n|^2\] となるから, \[\begin{aligned} k &= \frac{\vec n\cdot\overrightarrow{\mathrm P_0\mathrm H}}{|\vec n|^2} \\ &= \frac{a(p-x_0)+b(q-y_0)+c(r-z_0)}{a^2+b^2+c^2} \\ &= -\frac{ax_0+by_0+cz_0-(ap+bq+cr)}{a^2+b^2+c^2} \\ &= -\frac{ax_0+by_0+cz_0+d}{a^2+b^2+c^2} \end{aligned}\] が成り立つ. よって, 点 $\mathrm P_0$ と平面 $\alpha$ の距離は \[\begin{aligned} |\overrightarrow{\mathrm P_0\mathrm H}| &= |k\vec n| = |k||\vec n| \\ &= \frac{|ax_0+by_0+cz_0+d|}{a^2+b^2+c^2}\cdot\sqrt{a^2+b^2+c^2} \\ &= \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} \end{aligned}\] である.
- (2)
- (1) により, 原点と平面 $\mathrm{ABC}:\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c} = 1$ つまり
\[ bcx+cay+abz-abc = 0\]
の距離 $h$ は
\[ h = \frac{|-abc|}{\sqrt{(bc)^2+(ca)^2+(ab)^2}} = \frac{abc}{\sqrt{b^2c^2+c^2a^2+a^2b^2}}\]
である.
また, 三角錐 $\mathrm{OABC}$ の体積について \[\frac{1}{3}\triangle\mathrm{ABC}\cdot h = \frac{1}{3}\cdot\frac{ab}{2}\cdot c\] であるから, \[\begin{aligned} (\triangle\mathrm{ABC})^2 &= \left(\frac{abc}{2h}\right) ^2 = \frac{a^2b^2c^2}{4}\cdot\frac{1}{h^2} \\ &= \frac{a^2b^2c^2}{4}\cdot\frac{b^2c^2+c^2a^2+a^2b^2}{a^2b^2c^2} \\ &= \left(\frac{bc}{2}\right) ^2+\left(\frac{ca}{2}\right) ^2+\left(\frac{ab}{2}\right) ^2 \\ &= (\triangle\mathrm{OBC})^2+(\triangle\mathrm{OCA})^2+(\triangle\mathrm{OAB})^2 \end{aligned}\] が成り立つ.
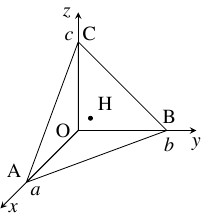
別解 1
- (2)
- $\overrightarrow{\mathrm{AB}} = (-a,b,0),$ $\overrightarrow{\mathrm{AC}} = (-a,0,c)$ から \[ |\overrightarrow{\mathrm{AB}}| = \sqrt{a^2+b^2}, \quad |\overrightarrow{\mathrm{AC}}| = \sqrt{a^2+c^2}, \quad \overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}} = a^2\] であるので, 三角形の面積の公式により, \[\begin{aligned} (\triangle\mathrm{ABC})^2 &= \frac{|\overrightarrow{\mathrm{AB}}|^2|\overrightarrow{\mathrm{AC}}|^2-(\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}})^2}{4} \\ &= \frac{(a^2+b^2)(a^2+c^2)-(a^2)^2}{4} \\ &= \frac{b^2c^2+c^2a^2+a^2b^2}{4} \\ &= \left(\frac{bc}{2}\right)^2+\left(\frac{ca}{2}\right)^2+\left(\frac{ab}{2}\right)^2 \\ &= (\triangle\mathrm{OBC})^2+(\triangle\mathrm{OCA})^2+(\triangle\mathrm{OAB})^2 \end{aligned}\] が成り立つ.
別解 2
- (2)
- 点 $\mathrm C$ から辺 $\mathrm{AB}$ に下ろした垂線の足を $\mathrm K$ とおく.
直角三角形 $\triangle\mathrm{OAB}$ に着目すると \[\triangle\mathrm{OAB} = \frac{1}{2}\mathrm{AB}\cdot\mathrm{OK} = \frac{1}{2}\mathrm{OA}\cdot\mathrm{OB}\] から \[\mathrm{OK} = \frac{\mathrm{OA}\cdot\mathrm{OB}}{\mathrm{AB}} = \frac{ab}{\sqrt{a^2+b^2}}\] が得られるので, 辺 $\mathrm{AB}$ を底辺としたときの $\triangle\mathrm{ABC}$ の高さは \[\begin{aligned} \mathrm{CK} &= \sqrt{\mathrm{OC}^2+\mathrm{OK}^2} = \sqrt{c^2+\frac{a^2b^2}{a^2+b^2}} \\ &= \sqrt{\frac{b^2c^2+c^2a^2+a^2b^2}{a^2+b^2}} \end{aligned}\] である. よって, \[\begin{aligned} (\triangle\mathrm{ABC})^2 &= \left(\frac{\mathrm{AB}\cdot\mathrm{CK}}{2}\right) ^2 = \frac{\mathrm{AB}^2}{4}\cdot\mathrm{CK}^2 \\ &= \frac{a^2+b^2}{4}\cdot\frac{b^2c^2+c^2a^2+a^2b^2}{a^2+b^2} \\ &= \left(\frac{bc}{2}\right) ^2+\left(\frac{ca}{2}\right) ^2+\left(\frac{ab}{2}\right) ^2 \\ &= (\triangle\mathrm{OBC})^2+(\triangle\mathrm{OCA})^2+(\triangle\mathrm{OAB})^2 \end{aligned}\] が成り立つ.
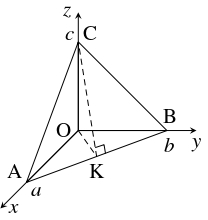
参考
一般に, $\angle\mathrm{BOC} = \angle\mathrm{COA} = \angle\mathrm{AOB} = 90^\circ$ なる三角錐 $\mathrm{OABC}$ (直角三角錐) に対して, (2) の等式が成り立つ.
これは, 「デカルト=グアの定理」(de Gua's Theorem) と呼ばれ, $3$ 次元空間における三平方の定理の類似である.
問題《球面の接平面の方程式》
原点 $\mathrm O$ を中心とする半径 $r$ の球面 $x^2+y^2+z^2 = r^2$ に点 $\mathrm P_0(x_0,y_0,z_0)$ で接する平面を $\alpha$ とおく.
点 $\mathrm P(x,y,z)$ に対して
\[\mathrm P \in \alpha \iff x_0x+y_0y+z_0z = r^2\]
が成り立つことを示せ.
解答例
点 $\mathrm P(x,y,z)$ に対して,
\[\begin{aligned}
\mathrm P \in \alpha &\iff \mathrm P = \mathrm P_0\text{ または }\overrightarrow{\mathrm{OP}_0} \perp \overrightarrow{\mathrm P_0\mathrm P} \\
&\iff \overrightarrow{\mathrm{OP}_0}\cdot\overrightarrow{\mathrm P_0\mathrm P} = 0 \\
&\iff (x_0,y_0,z_0)\cdot (x-x_0,y-y_0,z-z_0) = 0 \\
&\iff x_0x+y_0y+z_0z = x_0{}^2+y_0{}^2+z_0{}^2 \\
&\iff x_0x+y_0y+z_0z = r^2
\end{aligned}\]
が成り立つ.