双曲線
双曲線
定理《双曲線の標準形》
$a,$ $b > 0$ とする.
双曲線 $C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = \pm 1$ の中心は原点であり, $C$ は $x$ 軸, $y$ 軸, 原点に関して対称であって, $\dfrac{x}{a}\mp\dfrac{y}{b} = 0$ を漸近線にもつ.
- (i)
- 右辺が $1$ のとき. $C$ の焦点は $(\pm\sqrt{a^2+b^2},0),$ 頂点は $(\pm a,0)$ であり, $C$ の $2$ つの焦点から $C$ の各点までの距離の差は $2a$ である.
- (ii)
- 右辺が $-1$ のとき. $C$ の焦点は $(0,\pm\sqrt{b^2+a^2}),$ 頂点は $(0,\pm b)$ であり, $C$ の $2$ つの焦点から $C$ の各点までの距離の差は $2b$ である.
証明
(i), (ii) は互いに $x$ 座標, $y$ 座標を入れ替えた関係にあるから, (i) について, $c > 0$ として, 点 $\mathrm F(c,0),$ $\mathrm F'(-c,0)$ からの距離の差が $2a$ $(c > a)$ である点の軌跡 $C$ を求める.
$b = \sqrt{c^2-a^2}$ とおくと, 平面上の点 $\mathrm P(x,y)$ に対して,
\[\begin{aligned}
&\mathrm P \in C \\
&\!\!\!\!\iff \mathrm{PF}-\mathrm{PF}' = \pm 2a \iff \mathrm{PF} = \pm 2a+\mathrm{PF}' \\
&\!\!\!\!\iff \mathrm{PF}^2\! \!=\! (\pm 2a\!+\!\mathrm{PF}')^2\! \iff \mathrm{PF}^2\! \!=\! 4a^2\!\!\mp\!4a\mathrm{PF}'\!+\!\mathrm{PF}'^2 \\
&\!\!\!\!\iff (x\!-\!c)^2\!\!+\!y^2 \!\!=\! 4a^2\!\!\mp\!4a\sqrt{(x\!+\!c)^2\!\!+\!y^2}\!+\!(x\!+\!c)^2\!\!+\!y^2 \\
&\!\!\!\!\iff cx+a^2 = \mp a\sqrt{(x+c)^2+y^2} \\
&\!\!\!\!\iff (cx+a^2)^2 = a^2\{ (x+c)^2+y^2\} \\
&\!\!\!\!\iff (a^2-c^2)x^2-a^2y^2 = a^2(c^2-a^2) \\
&\!\!\!\!\iff b^2x^2-a^2y^2 = a^2b^2 \iff \frac{x^2}{a^2}-\frac{y^2}{b^2} = 1
\end{aligned}\]
となるから, $C$ の方程式は $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = 1$ である.
$(x,y) \in C$ のとき $(x,-y),$ $(-x,y),$ $(-x,-y) \in C$ となるから, $C$ は $x$ 軸, $y$ 軸, 原点に関して対称である. $c = \sqrt{a^2+b^2}$ であるから, $C$ の焦点は $(\pm\sqrt{a^2+b^2},0)$ である.
また, $C$ の頂点は座標軸との交点 $(\pm a,0)$ である.
さらに, 第 $1$ 象限において $C$ は, $y = \dfrac{b}{a}\sqrt{x^2-a^2}$ で表され, \[\begin{aligned} &\frac{b}{a}x-\frac{b}{a}\sqrt{x^2-a^2} = \frac{b}{a}(x-\sqrt{x^2-a^2}) \\ &= \frac{b}{a}\cdot\frac{(x+\sqrt{x^2-a^2})(x-\sqrt{x^2-a^2})}{x+\sqrt{x^2-a^2}} \\ &= \frac{b}{a}\cdot\frac{x^2-(x^2-a^2)}{x+\sqrt{x^2-a^2}} = \frac{ab}{x+\sqrt{x^2-a^2}} \\ &\to 0 \quad (x \to \infty ) \end{aligned}\] が成り立つから, $y = \dfrac{b}{a}x$ を漸近線にもつ. $C$ は, $x$ 軸, $y$ 軸, 原点に関して対称であるから, $\dfrac{x}{a}\mp\dfrac{y}{b} = 0$ を漸近線にもつ.
$(x,y) \in C$ のとき $(x,-y),$ $(-x,y),$ $(-x,-y) \in C$ となるから, $C$ は $x$ 軸, $y$ 軸, 原点に関して対称である. $c = \sqrt{a^2+b^2}$ であるから, $C$ の焦点は $(\pm\sqrt{a^2+b^2},0)$ である.
また, $C$ の頂点は座標軸との交点 $(\pm a,0)$ である.
さらに, 第 $1$ 象限において $C$ は, $y = \dfrac{b}{a}\sqrt{x^2-a^2}$ で表され, \[\begin{aligned} &\frac{b}{a}x-\frac{b}{a}\sqrt{x^2-a^2} = \frac{b}{a}(x-\sqrt{x^2-a^2}) \\ &= \frac{b}{a}\cdot\frac{(x+\sqrt{x^2-a^2})(x-\sqrt{x^2-a^2})}{x+\sqrt{x^2-a^2}} \\ &= \frac{b}{a}\cdot\frac{x^2-(x^2-a^2)}{x+\sqrt{x^2-a^2}} = \frac{ab}{x+\sqrt{x^2-a^2}} \\ &\to 0 \quad (x \to \infty ) \end{aligned}\] が成り立つから, $y = \dfrac{b}{a}x$ を漸近線にもつ. $C$ は, $x$ 軸, $y$ 軸, 原点に関して対称であるから, $\dfrac{x}{a}\mp\dfrac{y}{b} = 0$ を漸近線にもつ.
定理《双曲線の接線》
双曲線 $C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = \pm 1$ $(a,\ b > 0)$ の $C$ 上の点 $\mathrm P_0(x_0,y_0)$ における接線の方程式は
\[\frac{x_0x}{a^2}-\frac{y_0y}{b^2} = \pm 1\]
である.
証明
$\mathrm P_0 \neq (\pm a,0)$ のとき, $C$ の点 $\mathrm P_0$ における接線の傾きを $m$ とおく.
$C$ の方程式 $b^2x^2-a^2y^2 = \pm a^2b^2$ と接線の方程式
\[ y = mx+y_0-mx_0\]
から $y$ を消去して得られる $2$ 次方程式
\[ b^2x^2-a^2(mx+y_0-mx_0)^2 = \pm a^2b^2\]
つまり
\[\begin{aligned}
(b^2-a^2m^2)x^2&-2a^2m(y_0-mx_0)x \\
&-a^2\{(y_0-mx_0)^2\pm b^2\} = 0
\end{aligned}\]
は重解 $x = x_0$ をもつから,
\[\begin{aligned}
\frac{a^2m(y_0-mx_0)}{b^2-a^2m^2} &= x_0 \\
a^2m(y_0-mx_0) &= (b^2-a^2m^2)x_0 \\
m &= \dfrac{b^2x_0}{a^2y_0}
\end{aligned}\]
となる.
よって, 接線の方程式は
\[\begin{aligned}
y-y_0 &= \dfrac{b^2x_0}{a^2y_0}(x-x_0) \\
\frac{b^2x_0x}{a^2y_0}-y &= \frac{b^2x_0{}^2}{a^2y_0}-y_0 \\
\frac{x_0x}{a^2}-\frac{y_0y}{b^2} &= \frac{x_0{}^2}{a^2}-\frac{y_0{}^2}{b^2} \\
\frac{x_0x}{a^2}-\frac{y_0y}{b^2} &= \pm 1
\end{aligned}\]
である.
$\mathrm P_0 = (\pm a,0)$ のときの $C$ の接線の方程式 $x = \pm a$ もこの式で表される.
別証明
$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = \pm 1$ の両辺を $x$ で微分すると, $\dfrac{2x}{a^2}-\dfrac{2yy'}{b^2} = 0$ となり, $y \neq 0$ のとき
\[ y' = \frac{b^2x}{a^2y}\]
となる.
よって, $\mathrm P_0 \neq (\pm a,0)$ のとき, $C$ の点 $\mathrm P_0$ における接線の傾きは $\dfrac{b^2x_0}{a^2y_0}$ である.
以下, 上記の証明と同様である.
問題《双曲線の準円》
双曲線 $H:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = 1$ $(a > b > 0)$ に向かって互いに直交する $2$ 本の接線が引けるような点 $\mathrm P$ の軌跡を求めよ.
解答例
点 $(p,q)$ を通る傾き $m$ の直線 $y = m(x-p)+q$ が双曲線 $H:b^2x^2-a^2y^2 = a^2b^2$ に接するとする.
このとき,
\[\begin{aligned}
&b^2x^2-a^2\{ m(x-p)+q\} ^2 = a^2b^2 \\
&(b^2-a^2m^2)x^2+2a^2m(mp-q)x-a^2(mp-q)^2-a^2b^2 = 0
\end{aligned}\]
が重解をもつ $2$ 次方程式になるから,
であり,
\[\begin{aligned}
&a^4m^2(mp-q)^2+(b^2-a^2m^2)\{ a^2(mp-q)^2+a^2b^2\} = 0 \\
&a^2b^2\{ (mp-q)^2+b^2-a^2m^2\} = 0 \\
&(p^2-a^2)m^2-2pqm+b^2+q^2 = 0 \quad \cdots [2]
\end{aligned}\]
が成り立つ.
点 $\mathrm P(p,q)$ を通って傾きが $m_1,$ $m_2$ である $H$ の接線が直交するとき,
\[ p^2q^2-(p^2-a^2)(b^2+q^2) = a^2b^2-(b^2p^2-a^2q^2) > 0\]
であり, $[2]$ は相異なる $2$ つの実数解 $m = m_1,$ $m_2$ をもつから, 解と係数の関係により
\[\begin{aligned}
&-1 = m_1m_2 = \frac{b^2+q^2}{p^2-a^2} \\
&p^2+q^2 = a^2-b^2
\end{aligned}\]
が成り立つ.
ただし, $[1],$ $[2]$ から
\[\begin{aligned}
(p^2-a^2)\frac{b^2}{a^2}\mp 2pq\frac{b}{a}+b^2+q^2 &\neq 0 \\
b^2p^2\mp 2abpq+a^2q^2 &\neq 0
\end{aligned}\]
であるので,
である.
ゆえに, 点 $\mathrm P$ は原点を中心とする半径 $\sqrt{a^2-b^2}$ の円周を描く.
ただし, $H$ の漸近線との交点を除く.
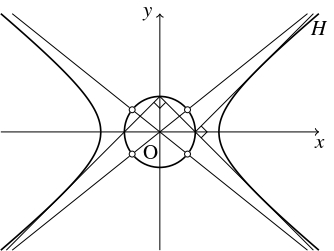
| $b^2-a^2m^2 \neq 0$ つまり $m \neq \pm\dfrac{b}{a} \quad \cdots [1]$ |
| $(bp\mp aq)^2 \neq 0$ つまり $q \neq \pm\dfrac{b}{a}p$ |

参考
- 双曲線 $H:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = 1$ $(a > b > 0)$ に対して, 円 $x^2+y^2 \leqq a^2-b^2$ を $H$ の「準円」(director circle) と呼ぶ.
- $2$ 次曲線は, $1$ つの焦点と「準円」の周または準線との距離が一定である点の軌跡として定まることが知られている.
問題《双曲線の焦点から発せられた光の反射》
双曲線 $C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = 1$ $(a,\ b > 0)$ の焦点を $\mathrm F_+(c,0),$ $\mathrm F_-(-c,0)$ $(c > 0)$ とおき,
$C$ 上に点 $\mathrm P(p,q)$ $(p > 0)$ をとる.
- (1)
- $a,$ $c,$ $p$ を用いて線分 $\mathrm F_+\mathrm P,$ $\mathrm F_-\mathrm P$ の長さを表せ.
- (2)
- $C$ の点 $\mathrm P$ における接線 $l$ と線分 $\mathrm F_+\mathrm P,$ $\mathrm F_-\mathrm P$ のなす角は等しいことを示せ.
解答例
- (1)
- $\dfrac{p^2}{a^2}-\dfrac{q^2}{b^2} = 1,$ $c^2 = a^2+b^2$ から, \[\begin{aligned} \mathrm F_\pm\mathrm P^2 &= (p\mp c)^2+q^2 = p^2\mp 2cp+c^2+b^2\left(\frac{p^2}{a^2}-1\right) \\ &= \left( 1+\frac{b^2}{a^2}\right) p^2\mp 2cp+(c^2-b^2) \\ &= \frac{c^2}{a^2}p^2\mp 2cp+a^2 = \left(\frac{c}{a}p\mp a\right) ^2 \end{aligned}\] である. $a \leqq p$ ($p > 0$ から従う) から \[\frac{c}{a}p\mp a \geqq \frac{c}{a}\cdot a\mp a = c\mp a > 0\] であるので, \[\mathrm F_\pm\mathrm P = \frac{c}{a}p\mp a\] である (以上, 複号同順).
- (2)
- 点 $\mathrm P$ が $C$ の頂点である場合, $l$ と線分 $\mathrm F_+\mathrm P,$ $\mathrm F_-\mathrm P$ のなす角は明らかに等しい. よって, その他の場合を考える. このとき, \[ l:\dfrac{px}{a^2}-\dfrac{qy}{b^2} = 1\] と $x$ 軸の交点を $\mathrm I$ とおくと, $\mathrm I\left(\dfrac{a^2}{p},0\right)$ から \[\begin{aligned} \mathrm F_+\mathrm I:\mathrm F_-\mathrm I &= \left( c-\frac{a^2}{p}\right) :\left(\frac{a^2}{p}+c\right) \\ &= (cp-a^2):(cp+a^2) \end{aligned}\] であり, (1) の結果により \[\begin{aligned} \mathrm F_+\mathrm P:\mathrm F_-\mathrm P &= \left(\frac{c}{a}p-a\right) :\left(\frac{c}{a}p+a\right) \\ &= (cp-a^2):(cp+a^2) \end{aligned}\] が成り立つので, $\mathrm F_+\mathrm I:\mathrm F_-\mathrm I = \mathrm F_+\mathrm P:\mathrm F_-\mathrm P$ となる. したがって, $l$ は $\angle\mathrm F_+\mathrm P\mathrm F_-$ を二等分するから, $l$ と線分 $\mathrm F_+\mathrm P,$ $\mathrm F_-\mathrm P$ のなす角は等しい.
問題《双曲線の接線の漸近線との交点と接点の関係》
双曲線 $C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = 1$ の接線が $C$ の漸近線によって切り取られてできる線分の中点は接点と一致することを示せ.
解答例
点 $\mathrm T(p,q)$ が双曲線 $C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = 1$ 上にあるとき,
\[\frac{p^2}{a^2}-\dfrac{q^2}{b^2} = 1 \quad \cdots [1]\]
が成り立つ.
このとき, $C$ の点 $\mathrm T$ における接線
\[\frac{p}{a^2}x-\frac{q}{b^2}y = 1\]
と $C$ の漸近線 $y = \dfrac{b}{a}x,$ $y = -\dfrac{b}{a}x$ はそれぞれ点
\[\mathrm P\left(\frac{a^2b}{bp-aq},\frac{ab^2}{bp-aq}\right),\ \mathrm Q\left(\frac{a^2b}{bp+aq},-\frac{ab^2}{bp+aq}\right)\]
で交わる.
線分 $\mathrm{PQ}$ の中点の $x$ 座標は
\[\begin{aligned}
&\frac{1}{2}\left(\frac{a^2b}{bp-aq}+\frac{a^2b}{bp+aq}\right) \\
&= \frac{1}{2}\cdot\frac{a^2b(bp+aq)+a^2b(bp-aq)}{(bp-aq)(bp+aq)} \\
&= \frac{1}{2}\cdot\frac{2a^2b^2p}{b^2p^2-a^2q^2} = \frac{a^2b^2p}{a^2b^2} \quad (\because [1]) \\
&= p,
\end{aligned}\]
線分 $\mathrm{PQ}$ の中点の $y$ 座標は
\[\begin{aligned}
&\frac{1}{2}\left(\frac{ab^2}{bp-aq}-\frac{ab^2}{bp+aq}\right) \\
&= \frac{1}{2}\cdot\frac{ab^2(bp+aq)-ab^2(bp-aq)}{(bp-aq)(bp+aq)} \\
&= \frac{1}{2}\cdot\frac{2a^2b^2q}{b^2p^2-a^2q^2} = \frac{a^2b^2q}{a^2b^2} \quad (\because [1]) \\
&= q
\end{aligned}\]
であるから, 点 $\mathrm T$ は線分 $\mathrm{PQ}$ の中点である.
別解
双曲線 $C$ の漸近線は, $1$ つの方程式
\[\frac{x^2}{a^2}-\frac{y^2}{b^2} = 0 \quad \cdots [1]\]
で表される.
$C$ の点 $\mathrm P(s,t)$ における接線の方程式は,
\[\frac{sx}{a^2}-\frac{ty}{b^2} = 1 \quad \cdots [2]\]
である.
$[1],$ $[2]$ の交点を $\mathrm Q,$ $\mathrm R$ とおく.
- (i)
- $t = 0$ のとき. 点 $\mathrm P$ は $x$ 軸上にあり, $C$ は $x$ 軸に関して対称であるから, 線分 $\mathrm{QR}$ の中点は点 $\mathrm P$ と一致する.
- (ii)
- $t \neq 0$ のとき. $[1],$ $[2]$ から $y$ を消去すると, \[ (b^2s^2-a^2t^2)x^2-2a^2b^2sx+a^4b^2 = 0 \quad \cdots [3]\] となる. また, 点 $\mathrm P$ は $C$ 上にあるから, \[\frac{s^2}{a^2}-\frac{t^2}{b^2} = 1 \quad \cdots [4]\] が成り立つ. $[3],$ $[4]$ から $a^2b^2x^2-2a^2b^2sx+a^4b^2 = 0$ であるので, \[ x^2-2sx+a^2 = 0 \quad \cdots [5]\] が成り立つ. $t \neq 0$ から $|s| > a$ であることに注意すると, $s^2-a^2 > 0$ から $[5]$ は確かに異なる $2$ つの実数解を持つ. その解を $\alpha,$ $\beta$ とおく. このとき, 解と係数の関係により $\alpha +\beta = 2s$ となるから, \[\frac{\alpha +\beta}{2} = s \quad \cdots [6]\] となる. $s,$ $\alpha,$ $\beta$ は点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ の $x$ 座標であるから, $[6]$ は線分 $\mathrm{QR}$ の中点が点 $\mathrm P$ と一致することを示している.
問題《双曲線の接線と漸近線が囲む三角形の面積》
双曲線 $C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = 1$ $(a > 0,\ b > 0)$ の接線と漸近線で囲まれてできる三角形の面積は一定であることを示せ.
解答例
点 $\mathrm T(p,q)$ が双曲線 $C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = 1$ 上にあるとき,
\[\frac{p^2}{a^2}-\dfrac{q^2}{b^2} = 1 \quad \cdots [1]\]
が成り立つ.
このとき, $C$ の点 $\mathrm T$ における接線
\[\frac{p}{a^2}x-\frac{q}{b^2}y = 1\]
と $C$ の漸近線 $y = \dfrac{b}{a}x,$ $y = -\dfrac{b}{a}x$ はそれぞれ点
\[\mathrm P\left(\frac{a^2b}{bp-aq},\frac{ab^2}{bp-aq}\right),\ \mathrm Q\left(\frac{a^2b}{bp+aq},-\frac{ab^2}{bp+aq}\right)\]
で交わる.
よって, $C$ の点 $\mathrm T$ における接線 $\mathrm{PQ}$ と漸近線で囲まれてできる三角形 $\mathrm{OPQ}$ の面積は
\[\begin{aligned}
&\frac{1}{2}\left|\frac{a^2b}{bp-aq}\cdot\left( -\frac{ab^2}{bp+aq}\right) -\frac{ab^2}{bp-aq}\cdot\frac{a^2b}{bp+aq}\right| \\
&= \frac{1}{2}\left|\frac{-2a^3b^3}{b^2p^2-a^2q^2}\right| = \frac{1}{2}\left|\frac{-2a^3b^3}{a^2b^2}\right| \quad (\because [1]) \\
&= \frac{1}{2}\cdot 2ab = ab
\end{aligned}\]
であり, 接点 $\mathrm T$ のとり方によらず一定である.
