曲線の媒介変数表示
曲線の媒介変数表示
問題《$2$ 次曲線の媒介変数表示》
$p \neq 0,$ $a > b > 0$ とする.
媒介変数表示
- (A)
- $x = pt^2,$ $y = 2pt$
- (B)
- (a)
- $x = a\cos\theta,$ $y = b\sin\theta$
- (b)
- $x = a\cdot\dfrac{1-t^2}{1+t^2},$ $y = b\cdot\dfrac{2t}{1+t^2}$
- (C)
- (a)
- $x = \dfrac{a}{\cos\theta},$ $y = b\tan\theta$
- (b)
- $x = a\cdot\dfrac{1+t^2}{1-t^2},$ $y = b\cdot\dfrac{2t}{1-t^2}$
- (c)
- $x = a\cdot\dfrac{t+t^{-1}}{2},$ $y = b\cdot\dfrac{t-t^{-1}}{2}$
解答例
- (A)
- $t = \dfrac{y}{2p}$ を $x = pt^2$ に代入すると \[ x = p\left(\frac{y}{2p}\right) ^2, \quad x = \frac{y^2}{4p}, \quad y^2 = 4px\] が得られるから, 媒介変数表示は点 $(p,0)$ を焦点, 直線 $x = -p$ を準線とする放物線を表す.
- (B)
- (a)
- \[\frac{x^2}{a^2}+\frac{y^2}{b^2} = \cos ^2\theta +\sin ^2\theta = 1\] であるから, 媒介変数表示は $2$ 点 $(\pm\sqrt{a^2-b^2},0)$ を焦点とする楕円の周を表す.
- (b)
- \[\begin{aligned} &\frac{x^2}{a^2}+\frac{y^2}{b^2} = \left(\frac{x}{a}\right) ^2+\left(\frac{y}{b}\right) ^2 \\ &= \left(\frac{1-t^2}{1+t^2}\right) ^2+\left(\frac{2t}{1+t^2}\right) ^2 = \frac{(1-t^2)^2+(2t)^2}{(1+t^2)^2} \\ &= \frac{(1-2t^2+t^4)+4t^2}{(1+t^2)^2} = \frac{1+2t^2+t^4}{(1+t^2)^2} \\ &= \frac{(1+t^2)^2}{(1+t^2)^2} = 1 \end{aligned}\] であるから, 媒介変数表示は $2$ 点 $(\pm\sqrt{a^2-b^2},0)$ を焦点とする楕円の周を表す.
- (C)
- (a)
- \[\frac{x^2}{a^2}-\frac{y^2}{b^2} = \frac{1}{\cos ^2\theta}-\tan ^2\theta = 1\] であるから, 媒介変数表示は $2$ 点 $(\pm\sqrt{a^2+b^2},0)$ を焦点とする双曲線を表す.
- (b)
- \[\begin{aligned} &\frac{x^2}{a^2}-\frac{y^2}{b^2} = \left(\frac{x}{a}\right) ^2-\left(\frac{y}{b}\right) ^2 \\ &= \left(\frac{1+t^2}{1-t^2}\right) ^2-\left(\frac{2t}{1-t^2}\right) ^2 = \frac{(1+t^2)^2-(2t)^2}{(1-t^2)^2} \\ &= \frac{(1+2t^2+t^4)-4t^2}{(1-t^2)^2} = \frac{1-2t^2+t^4}{(1-t^2)^2} \\ &= \frac{(1-t^2)^2}{(1-t^2)^2} = 1 \end{aligned}\] であるから, 媒介変数表示は $2$ 点 $(\pm\sqrt{a^2+b^2},0)$ を焦点とする双曲線を表す.
- (c)
- \[\begin{aligned} &\frac{x^2}{a^2}-\frac{y^2}{b^2} = \frac{(t+t^{-1})^2}{4}-\frac{(t-t^{-1})^2}{4} \\ &= \frac{(t^2+2+t^{-2})-(t^2-2+t^{-2})}{4} = 1 \end{aligned}\] であるから, 媒介変数表示は $2$ 点 $(\pm\sqrt{a^2+b^2},0)$ を焦点とする双曲線を表す.
参考
- (B), (C) の (a) において $t = \tan\dfrac{\theta}{2}$ とおくと, (b) が得られる.
- (C) の (c) において $t$ を $e^t$ に置き換えると, 双曲線の「双曲線関数」$\cosh t = \dfrac{e^t+e^{-t}}{2},$ $\sinh t = \dfrac{e^t-e^{-t}}{2}$ による媒介変数表示 \[ x = a\cosh t, \quad y = b\sinh t\] が得られる.
問題《サイクロイド》
$xy$ 平面において, 半径 $1$ の円が $0 \leqq y \leqq 2$ の部分をすべることなく転がる.
動円の中心を $\mathrm C,$ 動円と $x$ 軸の接点を $\mathrm T$ とおくとき,
原点 $\mathrm O$ を通過する動円の周上の定点 $\mathrm P(x,y)$ が描く軌跡の方程式を,
線分 $\mathrm{CP}$ の線分 $\mathrm{CT}$ からの回転角 $\theta$ を用いて表せ.
解答例
- $0 < \theta < 2\pi$ のとき.
$\mathrm{OT}$ は弧 $\mathrm{TP}$ の長さ $\theta$ に等しいから
\[\overrightarrow{\mathrm{OC}} = (\theta,1)\]
であり,
\[\begin{aligned}
\overrightarrow{\mathrm{CP}} &= \begin{cases}
(-\sin\theta,-\cos\theta) & \left( 0 < \theta < \dfrac{\pi}{2}\right), \\
(-\sin (\pi -\theta ),\cos (\pi -\theta )) & \left(\dfrac{\pi}{2} \leqq \theta < \pi\right), \\
(\sin (\theta -\pi ),\cos (\theta -\pi )) & \left(\pi \leqq \theta < \dfrac{3\pi}{2}\right), \\
(\sin (2\pi -\theta ),-\cos (2\pi -\theta )) & \left(\dfrac{3}{2}\pi \leqq \theta < 2\pi\right)
\end{cases} \\
&= (-\sin\theta,-\cos\theta )
\end{aligned}\]
である.
よって,
\[\begin{aligned}
\overrightarrow{\mathrm{OP}} &= \overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{CP}} \\
&= (\theta,1)+(-\sin\theta,-\cos\theta ) \\
&= (\theta -\sin\theta,1-\cos\theta )
\end{aligned}\]
が成り立つ.
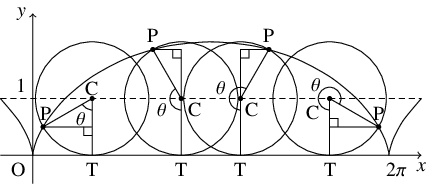
- これは, $\theta = 0$ のときも成り立つ.
参考
- 平面上において, 円が定直線に接しながらすべることなく転がるとき, 動円の周上の定点が描く軌跡を擺線またはサイクロイド (cycloid) と呼ぶ.
- サイクロイドは,「外サイクロイド」「内サイクロイド」「トコロイド」に一般化される. 「トコロイド」とは, 半径 $a$ の円が定直線に接しながらすべることなる転がるとき, 円の中心から距離 $b$ の位置にある定点が描く軌跡であり, \[ x = a\theta-b\sin\theta, \quad y = a-b\cos\theta\] と表される (証明は同様).
問題《外サイクロイドと内サイクロイド》
原点 $\mathrm O$ を中心とする半径 $a$ の円に, 点 $\mathrm C$ を中心とする半径 $b$ の円が, 接しながらすべることなく転がる.
- (i)
- 円 $\mathrm O$ に円 $\mathrm C$ が外接するとき
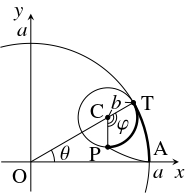
- (ii)
- 円 $\mathrm O$ に円 $\mathrm C$ が内接するとき
解答例
$\overrightarrow{\mathrm{OP}} = \overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{CP}}$ である.
円 $\mathrm O$ と円 $\mathrm C$ の接点を $\mathrm T$ とおき, 線分 $\mathrm{CP}$ の線分 $\mathrm{CT}$ からの回転角を $\varphi$ とおく.
このとき, 弧 $\mathrm{AT}$ と弧 $\mathrm{TP}$ の長さは等しいから,
が成り立つ.
| $a\theta = b\varphi$ つまり $\varphi = \dfrac{a}{b}\theta$ |
- (i)
- 円 $\mathrm O$ に円 $\mathrm C$ が外接するとき.
$\overrightarrow{\mathrm{OC}} = (a+b)(\cos\theta,\sin\theta )$ である.
また, 線分 $\mathrm{CP}$ の $x$ 軸の正方向からの回転角は
\[\theta +\pi +\varphi = \theta +\pi +\dfrac{a}{b}\theta = \pi +\dfrac{a+b}{b}\theta\]
であるから,
\[\overrightarrow{\mathrm{CP}} = -b\left(\cos\frac{a+b}{b}\theta ,\sin\frac{a+b}{b}\theta\right)\]
が成り立つ.
よって,
\[\begin{aligned}
x &= (a+b)\cos\theta -b\cos\frac{a+b}{b}\theta, \\
y &= (a+b)\sin\theta -b\sin\frac{a+b}{b}\theta
\end{aligned}\]
である.
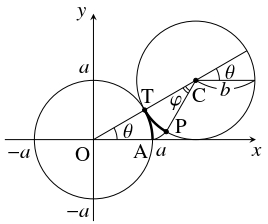
- (ii)
- 円 $\mathrm O$ に円 $\mathrm C$ が内接するとき.
$\overrightarrow{\mathrm{OC}} = (a-b)(\cos\theta,\sin\theta )$ である.
線分 $\mathrm{CP}$ の $x$ 軸の正方向からの回転角は
\[\theta -\varphi = \theta -\frac{a}{b}\theta = \frac{a-b}{-b}\theta\]
であるから,
\[\overrightarrow{\mathrm{CP}} = b\left(\cos\frac{a-b}{-b}\theta ,\sin\frac{a-b}{-b}\theta\right)\]
が成り立つ.
よって,
\[\begin{aligned}
x &= (a-b)\cos\theta +b\cos\frac{a-b}{-b}\theta, \\
y &= (a-b)\sin\theta +b\sin\frac{a-b}{-b}\theta
\end{aligned}\]
である.
参考
- 円が定円に外接しながらすべることなく転がるとき, 動円の周上の定点が描く軌跡を「外擺線」, 「外サイクロイド」または「エピサイクロイド」(epicycloid) と呼ぶ. 定円と動円の半径が等しい「外サイクロイド」を心臓形またはカージオイド (cardioid) と呼ぶ. カージオイドは「パスカルの蝸牛線」または「リマソン」と呼ばれる曲線の一種である.
- 円が定円に内接しながらすべることなく転がるとき, 動円の周上の定点が描く軌跡を「内擺線」, 「内サイクロイド」または「ハイポサイクロイド」(hypocycloid) と呼ぶ. 定円と動円の半径の比が $4:1$ の「内サイクロイド」を星芒形またはアストロイド (astroid) と呼ぶ (小惑星を意味するアステロイドではなく, アストロイドと呼ぶ方が好ましい). 上記の問題において $a = 1,$ $b = \dfrac{1}{4}$ とすると,「$3$ 倍角の公式」により, アストロイドの方程式 \[\begin{aligned} (x,y) &= \left(\frac{3}{4}\cos\theta +\frac{1}{4}\cos 3\theta,\frac{3}{4}\sin\theta -\frac{1}{4}\sin 3\theta\right) \\ \therefore (x,y) &= (\cos ^3\theta,\sin ^3\theta ) \end{aligned}\] が得られる.
