余弦定理・正弦定理
$\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C$ とおく.
余弦定理
定理《第一余弦定理》
$\triangle\mathrm{ABC}$ において,
\[\begin{aligned}
a &= b\cos C+c\cos B, \\
b &= c\cos A+a\cos C, \\
c &= a\cos B+b\cos A
\end{aligned}\]
が成り立つ.
証明
どれも同様に証明できるから, $c = a\cos B+b\cos A$ を示す.
$\triangle\mathrm{ABC}$ の頂点 $\mathrm C$ から辺 $\mathrm{AB}$ またはその延長に下ろした垂線の足を $\mathrm H$ とする.
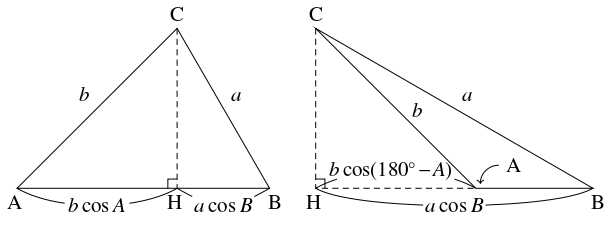
- (i)
- $A \leqq 90^\circ,$ $B \leqq 90^\circ$ のとき. \[ c = \mathrm{AH}+\mathrm{BH} = a\cos B+b\cos A\] が成り立つ.
- (ii)
- $A > 90^\circ$ のとき. \[\begin{aligned} c &= \mathrm{BH}-\mathrm{AH} = a\cos B-b\cos (180^\circ -A) \\ &= a\cos B-b(-\cos A) = a\cos B+b\cos A \end{aligned}\] が成り立つ.
- (iii)
- $B > 90^\circ$ のとき. (ii) の場合と同様に成り立つ.
定理《第二余弦定理》
$\triangle\mathrm{ABC}$ において,
\[\begin{aligned}
a^2 &= b^2+c^2-2bc\cos A, \\
b^2 &= c^2+a^2-2ca\cos B, \\
c^2 &= a^2+b^2-2ab\cos C
\end{aligned}\]
が成り立つ.
問題《第一余弦定理 $\Longrightarrow$ 第二余弦定理》
\[\begin{aligned}
a &= b\cos C+c\cos B, \\
b &= c\cos A+a\cos C, \\
c &= a\cos B+b\cos A
\end{aligned}\]
(第一余弦定理) から
\[\begin{aligned}
a^2 &= b^2+c^2-2bc\cos A, \\
b^2 &= c^2+a^2-2ca\cos B, \\
c^2 &= a^2+b^2-2ab\cos C
\end{aligned}\]
(第二余弦定理) を導け.
解答例
与式の辺々にそれぞれ $a,$ $-b,$ $-c$ を掛けると
\[\begin{aligned}
a^2 &= ab\cos C+ca\cos B, \\
-b^2 &= -bc\cos A-ab\cos C, \\
-c^2 &= -ca\cos B-bc\cos A
\end{aligned}\]
となるから, これらを加えると
\[\begin{aligned}
a^2-b^2-c^2 = &-2bc\cos A \\
a^2 = b^2+c^2&-2bc\cos A
\end{aligned}\]
が得られる.
残りの式も, 同様に得られる.
残りの式も, 同様に得られる.
参考
問題《マラルディの角度》
底辺の長さが $2\sqrt 2,$ 等辺の長さが $\sqrt 3$ である二等辺三角形の頂角の大きさを $\theta$ とおく.
$\cos\theta$ の値を求めよ.
解答例
余弦定理により,
\[\cos\theta = \frac{(\sqrt 3)^2+(\sqrt 3)^2-(2\sqrt 2)^2}{2\cdot\sqrt 3\cdot\sqrt 3} = -\frac{1}{3}\]
である.
参考
本問の角度 $\theta = 109.47122\cdots ^\circ = 109^\circ 28'16''\cdots$ は, 正四面体の中心と各頂点を結ぶ $4$ 本の直線が互いになす角度であり,「マラルディの角度」(Malardi's angle) として知られている.
この角度は,「空間充填図形」の $1$ つである「菱形十二面体」の面の頂角, A4 用紙の対角線のなす鈍角の大きさであり, 自然界ではガーネットの結晶, 石けんの泡, ミツバチの巣などに見ることができる.
問題《余弦定理による中線定理の証明》
$\triangle\mathrm{ABC}$ において, 辺 $\mathrm{BC}$ の中点を $\mathrm M$ とおく.
\[\mathrm{AB}^2+\mathrm{AC}^2 = 2(\mathrm{AM}^2+\mathrm{BM}^2) = 2(\mathrm{AM}^2+\mathrm{CM}^2)\]
が成り立つことを, 余弦定理を使って示せ.
解答例
$\theta = \angle\mathrm{AMB}$ とおく.
$\triangle\mathrm{ABM},$ $\triangle\mathrm{ACM}$ にそれぞれ余弦定理を適用すると,
$\mathrm{BM} = \mathrm{CM},$ $\cos (180^\circ -\theta ) = -\cos\theta$ から
\[\begin{aligned}
\mathrm{AB}^2 &= \mathrm{AM}^2+\mathrm{BM}^2-2\mathrm{AM}\cdot\mathrm{BM}\cos\theta, \\
\mathrm{AC}^2 &= \mathrm{AM}^2+\mathrm{CM}^2-2\mathrm{AM}\cdot\mathrm{CM}\cos (180^\circ -\theta ) \\
&= \mathrm{AM}^2+\mathrm{BM}^2+2\mathrm{AM}\cdot\mathrm{BM}\cos\theta
\end{aligned}\]
となる.
$2$ 式の辺々を加えると,
\[\mathrm{AB}^2+\mathrm{AC}^2 = 2(\mathrm{AM}^2+\mathrm{BM}^2) = 2(\mathrm{AM}^2+\mathrm{CM}^2)\]
が得られる.
参考
- 本問の結果は「中線定理」(parallelogram law) として知られている. これは「スチュワートの定理」(こちらを参照) に一般化される.
- 「中線定理」の別証明については, 距離の公式による証明 (こちら)と, ベクトルによる証明 (こちら), 複素数による証明 (こちら)も参照されたい.
- $\triangle\mathrm{ABC}$ の重心が $\mathrm G,$ $3$ 辺の長さが $\mathrm{BC} = a,$ $\mathrm{CA} = b,$ $\mathrm{AB} = c$ であるとき, $\mathrm{AG}:\mathrm{GM} = 2:1$ ($\mathrm M$: 辺 $\mathrm{BC}$ の中点) と「中線定理」により, \[\mathrm{AG} = \frac{\sqrt{2b^2+2c^2-a^2}}{3}\] であることがわかる.
問題《スチュワートの定理と角の二等分線の長さ》
- (1)
- $\triangle\mathrm{ABC}$ において, 辺 $\mathrm{BC}$ を $m:n$ に内分する点を $\mathrm D$ とおく. \[ n\mathrm{AB}^2+m\mathrm{AC}^2 = (m+n)\mathrm{AD}^2+n\mathrm{BD}^2+m\mathrm{CD}^2\] が成り立つことを示せ.
- (2)
- $\triangle\mathrm{ABC}$ において, $\angle\mathrm A$ の二等分線と辺 $\mathrm{BC}$ の交点を $\mathrm D$ とおく. また, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{CA}$ とおく. \[\begin{aligned} \mathrm{AD} &= \sqrt{\mathrm{AB}\cdot\mathrm{AC}-\mathrm{BD}\cdot\mathrm{CD}} \\ &= \frac{\sqrt{bc(b+c+a)(b+c-a)}}{b+c} \end{aligned}\] であることを示せ.
解答例
- (1)
- 略 (「中線定理」の証明と同様).
- (2)
- $\mathrm{BD}:\mathrm{DC} = c:b,$ $\mathrm{BD} = \dfrac{ac}{b+c},$ $\mathrm{CD} = \dfrac{ab}{b+c}$ であるから, (1) の結果により, \[\begin{aligned} (b+c)\mathrm{AD}^2 &= b\mathrm{AB}^2+c\mathrm{AC}^2-b\mathrm{BD}^2-c\mathrm{CD}^2 \\ &= bc^2+cb^2-b\cdot\frac{a^2c^2}{(b+c)^2}-c\cdot\frac{a^2b^2}{(b+c)^2} \\ &= bc(b+c)-\frac{a^2bc(b+c)}{(b+c)^2} \\ \mathrm{AD}^2 &= bc-\frac{ac}{b+c}\cdot\frac{ab}{b+c} \quad \cdots [1] \\ &= \mathrm{AB}\cdot\mathrm{AC}-\mathrm{BD}\cdot\mathrm{CD} \\ \mathrm{AD} &= \sqrt{\mathrm{AB}\cdot\mathrm{AC}-\mathrm{BD}\cdot\mathrm{CD}} \end{aligned}\] である. また, $[1]$ つまり \[\mathrm{AD} = bc\cdot\frac{(b+c)^2-a^2}{(b+c)^2} = \frac{bc(b+c+a)(b+c-a)}{(b+c)^2}\] から, \[\mathrm{AD} = \frac{\sqrt{bc(b+c+a)(b+c-a)}}{b+c}\] が得られる.
参考
問題《第一トレミーの定理》
辺の長さが $\mathrm{AB} = a,$ $\mathrm{BC} = b,$ $\mathrm{CD} = c,$ $\mathrm{DA} = d$ である四角形 $\mathrm{ABCD}$ が円に内接している.
$x = \mathrm{AC},$ $y = \mathrm{BD}$ とおく.
- (1)
- $a,$ $b,$ $c,$ $d$ を用いて $x,$ $y$ を表せ.
- (2)
- $xy = ac+bd$ が成り立つことを示せ.
解答例
- (1)
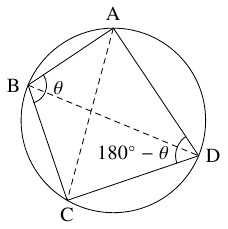
- $\angle\mathrm{ABC} = \theta$ とおく.
四角形 $\mathrm{ABCD}$ は円に内接しているから, このとき $\angle\mathrm{CDA} = 180^\circ -\theta$ である.
$\triangle\mathrm{ABC},$ $\triangle\mathrm{CDA}$ に余弦定理を適用すると, $x^2$ は \[\begin{aligned} x^2 &= a^2+b^2-2ab\cos\theta \quad \cdots [1], \\ x^2 &= c^2+d^2+2cd\cos\theta \quad \cdots [2] \end{aligned}\] と $2$ 通りに表せる. $[1]\times cd+[2]\times ab$ から \[\begin{aligned} (ab+cd)x^2 &= cd(a^2+b^2)+ab(c^2+d^2) \\ &= (ad+bc)(ac+bd) \\ x &= \sqrt{\frac{(ad+bc)(ac+bd)}{ab+cd}} \quad \cdots [3] \end{aligned}\] が得られる. $b$ と $d$ を入れ替えると, \[ y = \sqrt{\frac{(ab+cd)(ac+bd)}{ad+bc}} \quad \cdots [4]\] となる.
- (2)
- $[3]\times [4]$ から, \[\begin{aligned} xy &= \sqrt{\frac{(ab+cd)(ad+bc)(ac+bd)^2}{(ab+cd)(ad+bc)}} \\ &= ac+bd \end{aligned}\] が成り立つ.
参考
正弦定理
定理《正弦定理》
$\triangle\mathrm{ABC}$ において, 外接円の半径を $R$ とおくと,
\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R\]
が成り立つ.
参考
三角形の面積の公式
\[\triangle\mathrm{ABC} = \dfrac{1}{2}bc\sin A = \dfrac{1}{2}ca\sin B = \dfrac{1}{2}ab\sin C\]
から,
\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = \frac{abc}{2\triangle\mathrm{ABC}}\]
が直ちに得られる.
問題《第二余弦定理 $\Longrightarrow$ 正弦定理》
余弦定理 (第二余弦定理) から正弦定理
\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\]
を導け.
解答例
余弦定理により $\cos A = \dfrac{b^2+c^2-a^2}{2bc}$ であるから,
\[\sin ^2A = 1-\cos ^2A = 1-\frac{(b^2+c^2-a^2)^2}{(2bc)^2}\]
よって
\[\begin{aligned}
&(2bc\sin A)^2 = (2bc)^2-(b^2+c^2-a^2)^2 \\
&= (2bc+b^2+c^2-a^2)(2bc-b^2-c^2+a^2) \\
&= \{ (b+c)^2-a^2\}\{ a^2-(b-c)^2\} \\
&= (a+b+c)(-a+b+c)(a-b+c)(a+b-c)
\end{aligned}\]
が得られる.
右辺は $a,$ $b,$ $c$ に関する対称式であるから,
\[\begin{aligned}
(2bc\sin A)^2 &= (2ca\sin B)^2 = (2ab\sin C)^2 \\
2bc\sin A &= 2ca\sin B = 2ab\sin C \\
\frac{1}{2bc\sin A} &= \frac{1}{2ca\sin B} = \frac{1}{2ab\sin C} \\
\frac{a}{\sin A} &= \frac{b}{\sin B} = \frac{c}{\sin C}
\end{aligned}\]
が成り立つ.
参考
三角関数の加法定理 (数学 II) のもとで, 正弦定理, 余弦定理 (第一余弦定理, 第二余弦定理) は同値である (こちらとこちら, こちらを参照).
なお, ここでは, 正弦定理を「内角の正弦に対する対辺の長さの比が外接円の直径に等しい」という定理ではなく, 単に「内角の正弦に対する対辺の長さの比が互いに等しい」という定理として同値性を証明している.
問題《角の二等分線の性質》
$\triangle\mathrm{ABC}$ において, $\angle\mathrm A$ の内角の二等分線と辺 $\mathrm{BC}$ の交点を $\mathrm D$ とおく.
正弦定理を使って,
\[\mathrm{BD}:\mathrm{DC} = \mathrm{AB}:\mathrm{AC}\]
が成り立つことを示せ.
解答例
$\triangle\mathrm{ABD},$ $\triangle\mathrm{ACD}$ にそれぞれ正弦定理を適用すると
\[\begin{aligned}
\frac{\mathrm{BD}}{\sin\dfrac{A}{2}} &= \frac{\mathrm{AB}}{\sin\angle\mathrm{ADB}}, \\
\frac{\mathrm{DC}}{\sin\dfrac{A}{2}} &= \frac{\mathrm{AC}}{\sin\angle\mathrm{ADC}}
\end{aligned}\]
と得られるので, $\sin\angle\mathrm{ADB} = \sin\angle\mathrm{ADC}$ に注意すると
\[\frac{\mathrm{BD}}{\mathrm{DC}} = \frac{\mathrm{AB}}{\mathrm{AC}}\cdot\frac{\sin\angle\mathrm{ADC}}{\sin\angle\mathrm{ADB}} = \frac{\mathrm{AB}}{\mathrm{AC}}\]
つまり
\[\mathrm{BD}:\mathrm{DC} = \mathrm{AB}:\mathrm{AC}\]
が得られる.
問題《チャップル=オイラーの定理》
次のことを示せ.
- (1)
- 点 $\mathrm O$ を中心とする半径 $R$ の円周の弦 $\mathrm{XY}$ 上のすべての点 $\mathrm P$ に対して
\[\mathrm{OP}^2 = R^2-\mathrm{XP}\cdot\mathrm{YP}\]
が成り立つ.
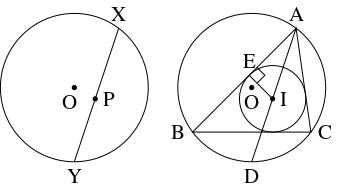
- (2)
- $\triangle\mathrm{ABC}$ の外心を $\mathrm O,$ 外接円の半径を $R,$ 内心を $\mathrm I,$ 内接円の半径を $r$ とおく.
さらに, 直線 $\mathrm{AI}$ と円周 $\mathrm O$ の交点のうち $\mathrm A$ と異なる方の点を $\mathrm D$ とおき, 辺 $\mathrm{AB}$ と円周 $\mathrm I$ の接点を $\mathrm E$ とおく.
このとき,
- ①
- $\mathrm{DB} = \mathrm{DI}$
- ②
- $\mathrm{AI}\cdot\mathrm{DB} = 2Rr$
- ③
- $\mathrm{OI}^2 = R^2-2Rr$
- ④
- $R \geqq 2r$
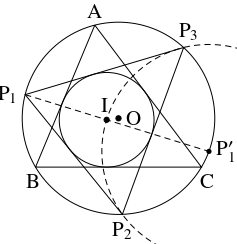
- (3)
- (2) の円周 $\mathrm O$ の上に点 $\mathrm P_1$ をとり, 直線 $\mathrm P_1\mathrm I$ と円周 $\mathrm O$ の交点のうち $\mathrm P_1$ と異なる方の点を $\mathrm P'_1$ とおく. さらに, $\mathrm I$ を通って $\mathrm P'_1$ を中心とする円周と円周 $\mathrm O$ の交点を $\mathrm P_2,$ $\mathrm P_3$ とおく. このとき, $\triangle\mathrm P_1\mathrm P_2\mathrm P_3$ の内心は $\mathrm I$ と一致する.
(参考: $2012$ 宮崎大)
解答例
- (1)
- 弦 $\mathrm{XY}$ の中点を $\mathrm M$ とおくと, 三平方の定理により \[\begin{aligned} \mathrm{OP}^2 &= \mathrm{OM}^2+\mathrm{MP}^2 \\ &= \mathrm{OX}^2-\mathrm{XM}^2+\mathrm{MP}^2 \\ &= R^2-(\mathrm{XM}+\mathrm{MP})(\mathrm{XM}-\mathrm{MP}) \\ &= R^2-(\mathrm{XM}+\mathrm{MP})(\mathrm{YM}-\mathrm{MP}) \\ &= R^2-\mathrm{XP}\cdot\mathrm{YP} \end{aligned}\] が得られる.
- (2)
- ①
- $\angle\mathrm{CAB} = 2\alpha,$ $\angle\mathrm{ABC} = 2\beta$ とおく. このとき, 円周角の定理により, \[\angle\mathrm{DBI} = \angle\mathrm{DBC}+\angle\mathrm{CBI} = \angle\mathrm{DAC}+\beta = \alpha +\beta\] が成り立つ. また, $\triangle\mathrm{ABI}$ の外角の関係から, \[\angle\mathrm{DIB} = \angle\mathrm{IAB}+\angle\mathrm{ABI} = \alpha +\beta\] が成り立つ. よって, $\triangle\mathrm{DBI}$ は $\angle\mathrm{DBI} = \angle\mathrm{DIB}$ なる二等辺三角形であるから, $\mathrm{DB} = \mathrm{DI}$ が成り立つ.
- ②
- 三角比の定義により, \[\mathrm{AI} = \frac{\mathrm{EI}}{\sin\alpha} = \frac{r}{\sin\alpha}\] が成り立つ. また, 正弦定理により, \[\mathrm{DB} = 2R\sin\alpha\] が成り立つ. よって, 辺々をかけると, \[\mathrm{AI}\cdot\mathrm{DB} = \frac{r}{\sin\alpha}\cdot 2R\sin\alpha = 2Rr\] が得られる.
- ③
- 円周 $\mathrm O$ の弦 $\mathrm{AD}$ と点 $\mathrm I$ に (1) を適用すると, ① と ② から \[\begin{aligned} \mathrm{OI}^2 &= R^2-\mathrm{AI}\cdot\mathrm{DI} \\ &= R^2-\mathrm{AI}\cdot\mathrm{DB} \\ &= R^2-2Rr \end{aligned}\] が得られる.
- ④
- ③ により \[ 0 \leqq \mathrm{OI}^2 = R(R-2r)\] であるから, $R-2r \geqq 0$ つまり $R \geqq 2r$ が成り立つ.
- (3)
- $\triangle\mathrm P_1\mathrm P_2\mathrm P_3$ の外心は $\mathrm O$ である.
また, $\mathrm P_1\mathrm I$ は $\angle\mathrm P_2\mathrm P_1\mathrm P_3$ の二等分線である.
さらに, 円周角の定理 (円周 $\mathrm P'_1,$ 円周 $\mathrm O$ に適用) により
\[\angle\mathrm{IP}_2\mathrm P_3 = \frac{\angle\mathrm{IP}'_1\mathrm P_3}{2} = \frac{\angle\mathrm P_1\mathrm P'_1\mathrm P_3}{2} = \frac{\angle\mathrm P_1\mathrm P_2\mathrm P_3}{2}\]
であるから, $\mathrm P_2\mathrm I$ は $\angle\mathrm P_1\mathrm P_2\mathrm P_3$ の二等分線である.
よって, $\mathrm I$ は $\triangle\mathrm P_1\mathrm P_2\mathrm P_3$ の内心である.
したがって, $\triangle\mathrm P_1\mathrm P_2\mathrm P_3$ の内接円の半径を $r'$ とおくと, (2) の ③ により
\[\mathrm{OI}^2 = R^2-2Rr = R^2-2Rr'\]
となり, $r = r'$ となる.
ゆえに, $\triangle\mathrm P_1\mathrm P_2\mathrm P_3$ の内心は $\mathrm I$ と一致する.
別解: 方べきの定理を利用
- (1)
- 直線 $\mathrm{OP}$ と円周 $\mathrm O$ の交点を $\mathrm Z,$ $\mathrm W$ とおくと, 方べきの定理により \[\begin{aligned} \mathrm{XP}\cdot\mathrm{YP} &= \mathrm{ZP}\cdot\mathrm{WP} \\ &= (R+\mathrm{OP})(R-\mathrm{OP}) \\ &= R^2-\mathrm{OP}^2 \end{aligned}\] となり, $\mathrm{OP}^2 = R^2-\mathrm{XP}\cdot\mathrm{YP}$ が得られる.
参考
- (2) の ③, ④ は「チャップル=オイラーの定理」(Chapple–Euler theorem) として知られている (初等幾何学的な証明についてはこちらを参照).
- (3) により, 次の定理が成り立つ: 円周 $C$ に内接し, 円周 $D$ に外接する三角形が存在するならば, $C$ 上の任意の点 $\mathrm P$ を $1$ つの頂点とし, $C$ に内接し, $D$ に外接する三角形が存在する. また, 円周 $C$ の中心が $\mathrm O,$ 半径が $R,$ 円周 $D$ の中心が $\mathrm I,$ 半径が $r$ であるとき, $C$ に内接し, $D$ に外接する三角形が存在するのは \[\mathrm{OI}^2 = R^2-2Rr\] が成り立つ場合に限る. これも「チャップルの定理」として知られている. さらに, これは, 次の「ポンスレの閉形定理」に一般化される: $2$ 次曲線 $C,$ $D$ に対して, $C$ に内接し, $D$ に外接する $n$ 角形が存在するとする. このとき, $C$ 上の任意の点 $\mathrm P_1$ を $1$ つの頂点とし, $C$ に内接し, $D$ に外接する $n$ 角形が存在する. つまり, $C$ 上の任意の点 $\mathrm P_1$ に対して, 点 $\mathrm P_k$ から $D$ に引いた接線と $C$ の交点 $(\neq \mathrm P_k)$ を $\mathrm P_{k+1}$ とおくことで点 $\mathrm P_2,$ $\cdots,$ $\mathrm P_n,$ $\mathrm P_{n+1}$ を順次定めると, $\mathrm P_{n+1} = \mathrm P_1$ となり, $C$ に内接し, $D$ に外接する $n$ 角形 $\mathrm P_1\mathrm P_2\cdots\mathrm P_n$ が得られる.
- $\triangle\mathrm{ABC}$ において, $\angle\mathrm A$ 内の傍接円の中心が $\mathrm I_{\mathrm A},$ 半径が $r_{\mathrm A}$ であるとき, \[\mathrm{OI}_{\mathrm A}{}^2 = R^2+2Rr_{\mathrm A}\] の成り立つことが知られている (証明は同様).