底面の対角線の長さは \[\sqrt{44^2+117^2} = \sqrt{15625} = 125\] であるから,「体対角線」の長さは \[\sqrt{125^2+240^2} = \sqrt{5^2(25^2+48^2)} = 5\sqrt{2929}\] である.

• 正四面体の対角線は存在しない. $1$ 辺の長さが $1$ の正四面体 $\mathrm{ABCD}$ の外接球の半径を $R$ とおく. また, 頂点 $\mathrm D$ から面 $\mathrm{ABC}$ に下ろした垂線の足を $\mathrm H$ とおく. 辺 $\mathrm{DH}$ を共有し, 斜辺の長さが等しい $3$ つの直角三角形 $\mathrm{ADH},$ $\mathrm{BDH},$ $\mathrm{CDH}$ は合同であるから, \[\mathrm{AH} = \mathrm{BH} = \mathrm{CH}\] である. よって, $\mathrm H$ は $\triangle\mathrm{ABC}$ の外心であるから, 正弦定理により \[\mathrm{AH} = \frac{1}{2\sin 60^\circ} = \frac{1}{\sqrt 3}\] である. 直角三角形 $\mathrm{ADH}$ に三平方の定理を適用すると, \[\mathrm{DH} = \sqrt{\mathrm{AD}^2-\mathrm{AH}^2} = \sqrt{1^2-\left(\frac{1}{\sqrt 3}\right) ^2} = \sqrt{\frac{2}{3}}\] が得られる. 垂線 $\mathrm{DH}$ は球の中心 $\mathrm O$ を通ることに注意して, 直角三角形 $\mathrm{AOH}$ に三平方の定理を適用すると, \[\left(\frac{1}{\sqrt 3}\right) ^2+\left(\sqrt{\frac{2}{3}}-R\right) ^2 = R^2, \quad 1-2\sqrt{\frac{2}{3}}R = 0\] よって \[ R = \frac{\sqrt 6}{4}\] が得られる.
• $1$ 辺の長さが $1$ の正六面体の最長対角線の長さ $d$ は \[ d = \sqrt{1^2+1^2+1^2} = \sqrt 3\] である. よって, 外接球の半径 $R$ は \[ R = \frac{d}{2} = \frac{\sqrt 3}{2}\] である.
• $1$ 辺の長さが $1$ の正八面体は $1$ 辺の長さが $2\cdot\dfrac{1}{\sqrt 2} = \sqrt 2$ の正六面体に内接するから, 最長対角線の長さ $d$ は \[ d = \sqrt 2\] である. よって, 外接球の半径 $R$ は \[ R = \frac{d}{2} = \frac{\sqrt 2}{2}\] である.
• $1$ 辺の長さが $1$ の正十二面体には $1$ 辺の長さが $\varphi = \dfrac{1+\sqrt 5}{2}$ の立方体(頂点を $1$ つ飛ばしに結んで得られる)が内接するから, 最長対角線の長さ $d$ は \[ d = \sqrt{\varphi ^2+\varphi ^2+\varphi ^2} = \varphi\sqrt 3 = \frac{\sqrt 3+\sqrt{15}}{2}\] である. よって, 外接球の半径 $R$ は \[ R = \frac{d}{2} = \frac{\sqrt 3+\sqrt{15}}{4}\] である.
• $1$ 辺の長さが $1$ の正二十面体の最長対角線は隣り合う $2$ 辺の長さが $1,$ $\varphi = \dfrac{1+\sqrt 5}{2}$ の長方形の対角線と一致するから, 最長対角線の長さ $d$ は \[ d = \sqrt{1^2+\varphi ^2} = \sqrt{1+\frac{3+\sqrt 5}{2}} = \sqrt{\frac{5+\sqrt 5}{2}} = \frac{\sqrt{10+2\sqrt 5}}{2}\] である. よって, 外接球の半径 $R$ は \[ R = \frac{d}{2} = \frac{\sqrt{10+2\sqrt 5}}{4}\] である.

　正多面体において, 中心(外接球, 内接球の中心), 頂点(外接球の接点), 面の中心(内接球の接点)は直角三角形をなす.

• $1$ 辺の長さが $1$ の正四面体において, 外接球の半径 $R$ は \[ R = \frac{\sqrt 6}{4}\] で(前問参照), 頂点と面の中心の距離 $l$ は面の外接球の半径に等しく \[ l = \frac{1}{2\sin 60^\circ} = \frac{1}{\sqrt 3}\] であるから, 内接球の半径 $r$ は三平方の定理により \[\begin{aligned} r &= \sqrt{R^2-l^2} = \sqrt{\left(\frac{\sqrt 6}{4}\right) ^2-\left(\frac{1}{\sqrt 3}\right) ^2} \\ &= \sqrt{\frac{3}{8}-\frac{1}{3}} = \sqrt{\frac{1}{24}} = \frac{\sqrt 6}{12} \end{aligned}\] である.
• $1$ 辺の長さが $1$ の正六面体の内接球の半径 $r$ は \[ r = \frac{1}{2}\] である.
• $1$ 辺の長さが $1$ の正八面体において, 外接球の半径 $R$ は \[ R = \frac{\sqrt 2}{2}\] で(前問参照), 頂点と面の中心の距離 $l$ は面の外接球の半径に等しく \[ l = \frac{1}{2\sin 60^\circ} = \frac{1}{\sqrt 3}\] であるから, 内接球の半径 $r$ は三平方の定理により \[\begin{aligned} r &= \sqrt{R^2-l^2} = \sqrt{\left(\frac{\sqrt 2}{2}\right) ^2-\left(\frac{1}{\sqrt 3}\right) ^2} \\ &= \sqrt{\frac{1}{2}-\frac{1}{3}} = \sqrt{\frac{1}{6}} = \frac{\sqrt 6}{6} \end{aligned}\] である.
• $1$ 辺の長さが $1$ の正十二面体において, 外接球の半径 $R$ は \[ R = \frac{\sqrt 3+\sqrt{15}}{4}\] で(前問参照), 頂点と面の中心の距離 $l$ は面の外接球の半径に等しく \[ l = \frac{1}{2\sin 36^\circ} = \frac{2}{\sqrt{10-2\sqrt 5}}\] であるから, 内接球の半径 $r$ は三平方の定理により \[\begin{aligned} r &= \sqrt{R^2-l^2} = \sqrt{\left(\frac{\sqrt 3+\sqrt{15}}{4}\right) ^2-\left(\frac{2}{\sqrt{10-2\sqrt 5}}\right) ^2} \\ &= \sqrt{\frac{18+6\sqrt 5}{16}-\frac{4}{10-2\sqrt 5}} = \sqrt{\frac{9+3\sqrt 5}{8}-\frac{40+8\sqrt 5}{80}} \\ &= \sqrt{\frac{25+11\sqrt 5}{40}} = \frac{1}{2}\sqrt{\frac{25+11\sqrt 5}{10}} \end{aligned}\] である.
• $1$ 辺の長さが $1$ の正二十面体において, 外接球の半径 $R$ は \[ R = \frac{\sqrt{10+2\sqrt 5}}{4}\] で(前問参照), 頂点と面の中心の距離 $l$ は面の外接球の半径に等しく \[ l = \frac{1}{2\sin 60^\circ} = \frac{1}{\sqrt 3}\] であるから, 内接球の半径 $r$ は三平方の定理により \[\begin{aligned} r &= \sqrt{R^2-l^2} = \sqrt{\left(\frac{\sqrt{10+2\sqrt 5}}{4}\right) ^2-\left(\frac{1}{\sqrt 3}\right) ^2} \\ &= \sqrt{\frac{10+2\sqrt 5}{16}-\frac{1}{3}} = \sqrt{\frac{14+6\sqrt 5}{48}} = \sqrt{\frac{(3+\sqrt 5)^2}{48}} \\ &= \frac{3+\sqrt 5}{4\sqrt 3} = \frac{3\sqrt 3+\sqrt{15}}{12} \end{aligned}\] である.

　$1$ 辺の長さが $1$ の正四面体の体積は \[\frac{\sqrt 2}{12}\cdot 1^3\] である. 内接球の半径を $r$ とおき, 正四面体を内心を頂点とする $4$ つの正三角錐に分けると, この体積は \[ 4\cdot\frac{1}{3}\left(\frac{1}{2}\cdot 1^2\cdot\frac{\sqrt 3}{2}\right) r = \frac{\sqrt 2}{12}\cdot 1^3\] と表せるから, \[ r = \frac{\sqrt 6}{12}\] である.

　$1$ 辺の長さが $1$ の正三角形, 正方形の面積は, それぞれ \[\begin{aligned} \frac{1}{2}\cdot 1^2\sin 60^\circ &= \frac{\sqrt 3}{4}, \\ 1^2 &= 1 \end{aligned}\] である. また, $1$ 辺の長さが $1$ の正五角形は, 半径 $\dfrac{1}{2}\div\sin 36^\circ = \dfrac{1}{2\sin 36^\circ}$ の円に内接するから, その面積は \[\begin{aligned} &5\cdot\frac{1}{2}\cdot\left(\frac{1}{2\sin 36^\circ}\right) ^2\sin 72^\circ = \frac{5}{8}\cdot\frac{16}{10-2\sqrt 5}\cdot\frac{\sqrt{10+2\sqrt 5}}{4} \\ &= \frac{5}{4}\cdot\frac{\sqrt{10+2\sqrt 5}}{5-\sqrt 5} = \frac{5}{4}\cdot\frac{\sqrt{10+2\sqrt 5}(5+\sqrt 5)}{(5-\sqrt 5)(5+\sqrt 5)} \\ &= \frac{5}{4}\cdot\frac{\sqrt{(10+2\sqrt 5)(5+\sqrt 5)^2}}{20} = \frac{\sqrt{(10+2\sqrt 5)(30+10\sqrt 5)}}{16} \\ &= \frac{\sqrt{400+160\sqrt 5}}{16} = \frac{\sqrt{25+10\sqrt 5}}{4} \end{aligned}\] である.

• $1$ 辺の長さが $1$ の正四面体は $1$ 辺の長さが $1$ の正三角形 $4$ 枚からなるから，その表面積 $S$ は \[ S = 4\cdot\frac{\sqrt 3}{2} = 2\sqrt 3\] である.
• $1$ 辺の長さが $1$ の正六面体は $1$ 辺の長さが $1$ の正方形 $6$ 枚からなるから，その表面積 $S$ は \[ S = 6\cdot 1 = 6\] である.
• $1$ 辺の長さが $1$ の正八面体は $1$ 辺の長さが $1$ の正三角形 $8$ 枚からなるから，その表面積 $S$ は \[ S = 8\cdot\frac{\sqrt 3}{2} = 4\sqrt 3\] である.
• $1$ 辺の長さが $1$ の正十二面体は $1$ 辺の長さが $1$ の正五角形 $12$ 枚からなるから，その表面積 $S$ は \[ S = 12\cdot\frac{\sqrt{25+10\sqrt 5}}{4} = 3\sqrt{25+10\sqrt 5}\] である.
• $1$ 辺の長さが $1$ の正二十面体は $1$ 辺の長さが $1$ の正三角形 $20$ 枚からなるから，その表面積 $S$ は \[ S = 20\cdot\frac{\sqrt 3}{2} = 10\sqrt 3\] である.

• $1$ 辺の長さが $1$ の正四面体は底面積が $\dfrac{\sqrt 3}{4},$ 高さが $\dfrac{\sqrt 6}{12}$ (内接球の半径)の正三角錐 $4$ 個に分けられるから, その体積 $V$ は \[ V = 4\cdot\left(\frac{1}{3}\cdot\frac{\sqrt 3}{4}\cdot\frac{\sqrt 6}{12}\right) = \frac{\sqrt 2}{12}\] である.
• $1$ 辺の長さが $1$ の正六面体の体積 $V$ は \[ V = 1^3 = 1\] である.
• $1$ 辺の長さが $1$ の正八面体は辺の長さが $\dfrac{\sqrt 2}{2}$ の $3$ 辺が直角に交わるような正三角錐 $8$ 個に分けられるから, その体積 $V$ は \[ V = 8\cdot\left\{\frac{1}{3}\cdot\frac{1}{2}\left(\frac{\sqrt 2}{2}\right) ^2\cdot\frac{\sqrt 2}{2}\right\} = \frac{\sqrt 2}{3}\] である.
• $1$ 辺の長さが $1$ の正十二面体は底面積が $\dfrac{\sqrt{25+10\sqrt 5}}{4},$ 高さが $\dfrac{1}{2}\sqrt{\dfrac{25+11\sqrt 5}{10}}$ (内接球の半径)の正五角錐 $12$ 個に分けられるから, その体積 $V$ は \[\begin{aligned} V &= 12\cdot\left(\frac{1}{3}\cdot\frac{\sqrt{25+10\sqrt 5}}{4}\cdot\frac{1}{2}\sqrt{\frac{25+11\sqrt 5}{10}}\right) \\ &= \frac{1}{2}\sqrt{\frac{(25+10\sqrt 5)(25+11\sqrt 5)}{10}} = \frac{1}{2}\sqrt{\frac{1175+525\sqrt 5}{10}} \\ &= \frac{1}{2}\sqrt{\frac{470+210\sqrt 5}{4}} = \frac{\sqrt{(15+7\sqrt 5)^2}}{4} = \frac{15+7\sqrt 5}{4} \end{aligned}\] である.
• $1$ 辺の長さが $1$ の正二十面体は底面積が $\dfrac{\sqrt 3}{4},$ 高さが $\dfrac{3\sqrt 3+\sqrt{15}}{12}$ (内接球の半径)の正三角錐 $20$ 個に分けられるから, その体積 $V$ は \[ V = 20\cdot\left(\frac{1}{3}\cdot\frac{\sqrt 3}{4}\cdot\frac{3\sqrt 3+\sqrt{15}}{12}\right) = \frac{15+5\sqrt 5}{12}\] である.

• $1$ 辺の長さが $1$ の正四面体 $\mathrm{ABCD}$ において, 辺 $\mathrm{AB}$ の中点を $\mathrm M$ とおく. このとき, $\mathrm{CD} = 1,$ $\mathrm{CM} = \mathrm{DM} = \dfrac{\sqrt 3}{2}$ となるから, 余弦定理により \[\cos\angle\mathrm{CMD} = \frac{\left(\dfrac{\sqrt 3}{2}\right) ^2+\left(\dfrac{\sqrt 3}{2}\right) ^2-1^2}{2\cdot\dfrac{\sqrt 3}{2}\cdot\dfrac{\sqrt 3}{2}} = \frac{1}{3}\] となり, \[\sin\angle\mathrm{CMD} = \sqrt{1^2-\cos ^2\angle\mathrm{CMD}} = \sqrt{1^2-\left(\frac{1}{3}\right) ^2} = \frac{2\sqrt 2}{3}\] となる. よって, $1$ 辺の長さが $1$ の正四面体の体積 $V$ は \[ V = \frac{1}{3}\cdot\left(\frac{1}{2}\cdot 1^2\cdot\frac{\sqrt 3}{2}\right) \cdot\left(\frac{\sqrt 3}{2}\cdot\frac{2\sqrt 2}{3}\right) = \frac{\sqrt 2}{12}\] である.
• $1$ 辺の長さが $1$ の正八面体は底面の $1$ 辺の長さが $1,$ 高さが $\dfrac{\sqrt 2}{2}$ の正四角錐 $2$ 個に分けられるから, その体積 $V$ は \[ V = 2\cdot\left(\dfrac{1}{3}\cdot 1^2\cdot\frac{\sqrt 2}{2}\right) = \frac{\sqrt 2}{3}\] である.

　正四面体 $\mathrm{ABCD}$ の $1$ 辺の長さを $a$ とおく. また, 頂点 $\mathrm D$ から面 $\mathrm{ABC}$ に下ろした垂線の足を $\mathrm H$ とおく. 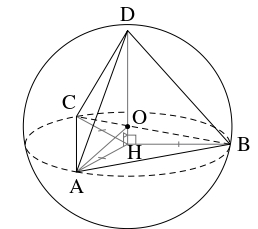辺 $\mathrm{DH}$ を共有し, 斜辺の長さが等しい $3$ つの直角三角形 $\mathrm{ADH},$ $\mathrm{BDH},$ $\mathrm{CDH}$ は合同であるから, \[\mathrm{AH} = \mathrm{BH} = \mathrm{CH}\] である. よって, $\mathrm H$ は $\triangle\mathrm{ABC}$ の外心であるから, 正弦定理により, \[\mathrm{AH} = \frac{a}{2\sin 60^\circ} = \frac{a}{\sqrt 3}\] である. 直角三角形 $\mathrm{ADH}$ に三平方の定理を適用すると, \[\mathrm{DH} = \sqrt{\mathrm{AD}^2-\mathrm{AH}^2} = \sqrt{a^2-\left(\frac{a}{\sqrt 3}\right) ^2} = \frac{\sqrt 6}{3}a \quad \cdots [1]\] が得られる. 垂線 $\mathrm{DH}$ は球の中心 $\mathrm O$ を通ることに注意して, 直角三角形 $\mathrm{AOH}$ に三平方の定理を適用すると, \[\left(\frac{a}{\sqrt 3}\right) ^2+\left(\frac{\sqrt 6}{3}a-1\right) ^2 = 1^2, \quad a^2-\frac{2\sqrt 6}{3}a = 0\] よって \[ a = \frac{2\sqrt 6}{3} \quad \cdots [2]\] が得られる. したがって, \[\begin{aligned} \triangle\mathrm{ABC} &= \frac{1}{2}a^2\sin 60^\circ = \frac{1}{2}\left(\frac{2\sqrt 6}{3}\right)^2\frac{\sqrt 3}{2} = \frac{2\sqrt 3}{3}, \\ \mathrm{DH} &= \frac{\sqrt 6}{3}\cdot\frac{2\sqrt 6}{3} = \frac{4}{3} \end{aligned}\] であるから, \[ V = \frac{1}{3}\triangle\mathrm{ABC}\cdot\mathrm{DH} = \frac{1}{3}\cdot\frac{2\sqrt 3}{3}\cdot\frac{4}{3} = \frac{8\sqrt 3}{27}\] である.

　正四面体 $\mathrm{ABCD}$ の $1$ 辺の長さを $a$ とおく. また, 辺 $\mathrm{AB}$ の中点を $\mathrm M$ とおく. このとき, \[\mathrm{CM} = \mathrm{DM} = \frac{\sqrt 3}{2}a\] となる. $\theta = \angle\mathrm{CMD}$ とおき, $\triangle\mathrm{CDM}$ において余弦定理を適用すると, \[\begin{aligned} \cos\theta &= \frac{\left(\dfrac{\sqrt 3}{2}a\right) ^2+\left(\dfrac{\sqrt 3}{2}a\right) ^2-a^2}{2\cdot\dfrac{\sqrt 3}{2}a\cdot\dfrac{\sqrt 3}{2}a} \\ &= \frac{(\sqrt 3)^2+(\sqrt 3)^2-2^2}{2\cdot\sqrt 3\cdot\sqrt 3} = \frac{1}{3}, \\ \sin\theta &= \sqrt{1-\cos ^2\theta} = \sqrt{1-\left(\frac{1}{3}\right) ^2} = \frac{2\sqrt 2}{3} \end{aligned}\] が得られる. よって, 頂点 $\mathrm D$ から面 $\mathrm{ABC}$ に下ろした垂線の足を $\mathrm H$ とおくと, \[\mathrm{DH} = \mathrm{DM}\sin\theta = \frac{\sqrt 3}{2}a\cdot\frac{2\sqrt 2}{3} = \frac{\sqrt 6}{3}a \quad \cdots [1]\] となる. 以下, 解答例と同様.

　球の中心を $\mathrm O$ とおく. $4$ つの四面体 $\mathrm{OABC},$ $\mathrm{OBCD},$ $\mathrm{OCDA},$ $\mathrm{ODAB}$ は合同である. よって, その体積を $W$ とおくと $V = 4W$ となるので, \[\dfrac{1}{3}\triangle\mathrm{ABC}\cdot\mathrm{DH} = 4\cdot\frac{1}{3}\triangle\mathrm{ABC}\cdot\mathrm{OH}\] から \[\mathrm{DH} = 4\mathrm{OH}\] が得られる. 垂線 $\mathrm{DH}$ が点 $\mathrm O$ を通ることに注意すると, \[\begin{aligned} \mathrm{DH} &= \frac{4}{3}\mathrm{OD} = \frac{4}{3}, \\ a &= \frac{3}{\sqrt 6}\mathrm{DH} = \frac{3}{\sqrt 6}\cdot\frac{4}{3} = \frac{2\sqrt 6}{3} \end{aligned}\] が得られる. 以下, 解答例と同様.

　$1$ 辺の長さが $a$ の正四面体 $\mathrm{ABCD}$ は $1$ 辺の長さが $\dfrac{a}{\sqrt 2}$ の立方体 $\mathrm{AKDL}\text{-}\mathrm{MBNC}$ に内接させることができる. 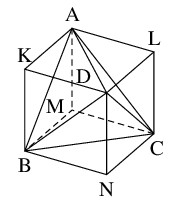よって, 正四面体 $\mathrm{ABCD}$ はこの立方体から $4$ 個の合同な三角錐を取り除いたものであり, 各三角錐の体積は立方体の体積 $W$ の $\dfrac{1}{6}$ にあたるから, 求める体積は, \[\begin{aligned} V &= W-4\cdot\frac{W}{6} = \frac{1}{3}W = \frac{1}{3}\left(\frac{a}{\sqrt 2}\right) ^3 = \frac{\sqrt 2}{12}a^3 \\ &= \frac{\sqrt 2}{12}\left(\frac{2\sqrt 6}{3}\right) ^3 = \frac{8\sqrt 3}{27} \end{aligned}\] である.

(1)

$a,$ $b,$ $c$ を面の対角線の長さとする直方体の存在, つまり \[y^2+z^2 = a^2, \quad z^2+x^2 = b^2, \quad x^2+y^2 = c^2\] なる正の数 $x,$ $y,$ $z$ の存在を示せばよい.

これら $3$ 式の辺々を加えて両辺を $2$ で割ると \[ x^2+y^2+z^2 = \frac{a^2+b^2+c^2}{2}\] となるから, これは \[\begin{aligned} x^2 &= \dfrac{b^2+c^2-a^2}{2}, \\ y^2 &= \dfrac{c^2+a^2-b^2}{2}, \\ z^2 &= \dfrac{a^2+b^2-c^2}{2} \end{aligned}\] と同値であり, 条件からこれら $3$ 式の右辺は正であることに注意すると, \[\begin{aligned} x &= \sqrt{\frac{b^2+c^2-a^2}{2}}, \\ y &= \sqrt{\frac{c^2+a^2-b^2}{2}}, \\ z &= \sqrt{\frac{a^2+b^2-c^2}{2}} \end{aligned}\] が条件を満たすことがわかる.

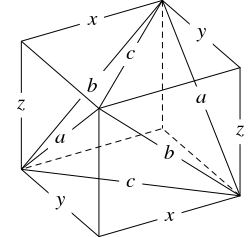
(2)

$T$ は (1) の直方体から $4$ つの角(互いに合同な三角錐)を取り除いて得られるから, その体積は \[\begin{aligned} V &= xyz-4\cdot\frac{1}{3}\cdot\frac{1}{2}xy\cdot z = \frac{1}{3}xyz \\ &= \frac{\sqrt{2(b^2+c^2-a^2)(c^2+a^2-b^2)(a^2+b^2-c^2)}}{12} \end{aligned}\] である.

(3)

$T$ の外接球の直径は (1) の直方体の対角線の長さに等しいから, $T$ の外接球の半径は \[ R = \frac{1}{2}\sqrt{x^2+y^2+z^2} = \sqrt{\frac{a^2+b^2+c^2}{8}}\] である.

(4)

$T$ の表面積は,「ヘロンの公式」により, \[\begin{aligned} S &= 4\triangle\mathrm{ABC} \\ &= \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \end{aligned}\] である.

(5)

$V = \dfrac{1}{3}Sr$ であるから, $T$ の内接球の半径は \[\begin{aligned} r &= \frac{3V}{S} \\ &= \sqrt{\frac{(b^2+c^2-a^2)(c^2+a^2-b^2)(a^2+b^2-c^2)}{8(a+b+c)(b+c-a)(c+a-b)(a+b-c)}} \end{aligned}\] である.