接線・法線 (理系)
接線
定理《関数のグラフの接線》
$x = \alpha$ において微分可能な関数 $f(x)$ のグラフ $y = f(x)$ の点 $(\alpha ,f(\alpha ))$ における接線の方程式は
\[ y-f(\alpha ) = f'(\alpha )(x-\alpha )\]
である.
問題《座標軸が切り取るアストロイドの接線》
媒介変数表示された曲線
\[ C:\begin{cases}
x = \cos ^3t, & {} \\
y = \sin ^3t & {}
\end{cases}\]
の $t$ ($\neq \dfrac{n\pi}{2},$ $n$: 整数) に対応する点での接線が座標軸によって切り取られてできる線分の長さは,
$t$ の値によらず一定であることを示せ.
解答例
$t \neq \dfrac{n\pi}{2}$ ($n$: 整数) とする.
このとき,
\[\frac{dy}{dx} = \frac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}} = \frac{3\sin ^2t\cos t}{-3\cos ^2t\sin t} = -\tan t\]
であるから, 点 $(\cos ^3t,\sin ^3t)$ における $C$ の接線の方程式は
\[ y = -\tan t(x-\cos ^3t)+\sin ^3t\]
である.
この $x$ 切片は
\[\begin{aligned}
0 &= -\tan t(x-\cos ^3t)+\sin ^3t \\
\tan t(x-\cos ^3t) &= \sin ^3t \\
x-\cos ^3t &= \frac{\sin ^3t}{\tan t} = \cos t\sin ^2t
\end{aligned}\]
から
\[ x = \cos ^3t+\cos t\sin ^2t = \cos t(\cos ^2t+\sin ^2t) = \cos t\]
であり, $y$ 切片は
\[\begin{aligned}
y &= -\tan t(-\cos ^3t)+\sin ^3t = \sin t\cos ^2t+\sin ^3t \\
&= \sin t(\cos ^2t+\sin ^2t) = \sin t
\end{aligned}\]
である.
ゆえに, $C$ の接線が座標軸によって切り取られてできる線分の長さは
\[\sqrt{(0-\cos t)^2+(\sin t-0)^2} = 1\]
で, $t$ の値によらず一定である.
参考
- $x^{\frac{2}{3}}+y^{\frac{2}{3}} \leqq a^{\frac{2}{3}}$ で表される領域, または曲線 $x^{\frac{2}{3}}+y^{\frac{2}{3}} = a^{\frac{2}{3}}$ $(a > 0)$ を「星芒形」または「アストロイド」(asteroid) と呼ぶ (小惑星を意味するアステロイドではなく, アストロイドと呼ぶ方が好ましい).
- 領域 $x^{\frac{2}{3}}+y^{\frac{2}{3}} \leqq a^{\frac{2}{3}}$ は, $x$ 軸と $y$ 軸の両方に接する長さ $a$ の線分の通過範囲として定まる (こちらも参照).
- 曲線 $x^{\frac{2}{3}}+y^{\frac{2}{3}} = a^{\frac{2}{3}}$ は, 半径 $a$ の定円の中をその周に沿って半径 $\dfrac{a}{4}$ の円がすべることなく転がるとき, 動円の周上の $1$ 点の軌跡としても定まる (こちらを参照).
問題《牽引線の接線の性質》
媒介変数表示された曲線
\[ C:\begin{cases}
x = \cos\theta +\log\tan\dfrac{\theta}{2}, & {} \\
y = \sin\theta & {}
\end{cases} \quad (0 < \theta < \pi )\]
の $\theta \neq \dfrac{\pi}{2}$ なる実数 $\theta$ に対応する点 $\mathrm P$ における接線と $x$ 軸との交点を $\mathrm M$ とおく.
線分 $\mathrm{MP}$ の長さは $\mathrm P$ のとり方によらず一定であることを示せ.
(参考: $2004$ 旭川医科大)
解答例
\[\begin{aligned}
\frac{dx}{d\theta} &= -\sin\theta +\frac{1}{\tan\dfrac{\theta}{2}}\cdot\frac{1}{\cos ^2\dfrac{\theta}{2}}\cdot\frac{1}{2} \\
&= -\sin\theta +\frac{1}{2\sin\dfrac{\theta}{2}\cos\dfrac{\theta}{2}} \quad \left(\because\tan\frac{\theta}{2} = \frac{\sin\dfrac{\theta}{2}}{\cos\dfrac{\theta}{2}}\right) \\
&= -\sin\theta +\frac{1}{\sin\theta}, \\
\frac{dy}{d\theta} &= \cos\theta
\end{aligned}\]
であるから,
\[\begin{aligned}
\frac{dy}{dx} &= \frac{\dfrac{dy}{d\theta}}{\dfrac{dx}{d\theta}} = \frac{\cos\theta}{-\sin\theta +\dfrac{1}{\sin\theta}} = \frac{\sin\theta\cos\theta}{-\sin ^2\theta +1} \\
&= \frac{\sin\theta\cos\theta}{\cos^2\theta} = \tan\theta
\end{aligned}\]
である.
よって, 実数 $\theta$ に対応する点 $\mathrm P$ における $C$ の接線は
\[ y = \tan\theta\left( x-\cos\theta -\log\tan\frac{\theta}{2}\right) +\sin\theta\]
であり, その $x$ 軸との交点 $\mathrm M$ の $x$ 座標は
\[\begin{aligned}
&\tan\theta\left( x-\cos\theta -\log\tan\frac{\theta}{2}\right) +\sin\theta = 0 \\
&\left( x-\cos\theta -\log\tan\frac{\theta}{2}\right) +\cos\theta = 0
\end{aligned}\]
の解
\[ x = \log\tan\frac{\theta}{2}\]
である.
よって,
\[\begin{aligned}
\mathrm{MP} &= \sqrt{\left\{\left(\cos\theta +\log\tan\frac{\theta}{2}\right) -\log\tan\frac{\theta}{2}\right\} ^2+(\sin\theta -0)^2} \\
&= \sqrt{\cos ^2\theta +\sin ^2\theta} = 1
\end{aligned}\]
であり, この値は $\mathrm P$ のとり方によらず一定である.
参考
- \[\begin{cases}
x = a\left(\cos\theta +\log\tan\dfrac{\theta}{2}\right), & {} \\
y = a\sin\theta & {}
\end{cases} \quad (0 < \theta < \pi )\]
($a$: 正の数) で定まる曲線を「牽引線」または「トラクトリックス」(tractrix) と呼ぶ.
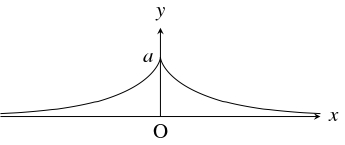
- 犬と飼い主が伸び縮みのしない長さ $a$ のリードでつながれた状態から, 飼い主が犬を引っ張りながら原点から $x$ 軸上を移動するとき, 点 $(0,a)$ にいた犬が描く軌跡は「牽引線」である (こちらを参照).
- 伸び縮みのしないひもをある図形にたるみなく巻きつけていくとき, またはそれをたるみなくほどいていくとき, ひもの先端が描く軌跡はその図形の「伸開線」または「インボリュート」(involute) と呼ばれる. 「牽引線」は「懸垂線」$y = a\cdot\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}$ ($a$: 正の数) の「伸開線」であることとが知られている.
問題《楕円曲線の有理点から別の有理点を得る方法》
$a,$ $b,$ $c$ を有理数とし, $xy$ 平面において曲線
\[ E:y^2 = x^3+ax^2+bx+c\]
上に $x$ 座標も $y$ 座標も有理数である $2$ 点 $\mathrm P_1(x_1,y_1),$ $\mathrm P_2(x_2,y_2)$ が存在するとする.
$x_1 \neq x_2$ のとき直線 $\mathrm P_1\mathrm P_2$ を, $\mathrm P_1 = \mathrm P_2$ かつ $y_1 \neq 0$ のとき $E$ の点 $\mathrm P_1$ における接線を, 直線 $l:y = mx+n$ ($m,$ $n$: 実数) とする.
さらに, 曲線 $E$ と直線 $l$ の交点を $\mathrm P_3(x_3,y_3)$ とおく.
このとき, 次のことを示せ.
- (1)
- $m$ も $n$ も有理数である.
- (2)
- $x_3$ も $y_3$ も有理数である.
解答例
- (1)
- (i)
- $x_1 \neq x_2$ のとき. 仮定により $x_1,$ $y_1,$ $x_2,$ $y_2$ は有理数であるから, $l$ つまり直線 $\mathrm P_1\mathrm P_2$ の傾き \[ m = \frac{y_2-y_1}{x_2-x_1}\] は有理数である.
- (ii)
- $\mathrm P_1 = \mathrm P_2$ かつ $y_1 \neq 0$ のとき. $y^2 = x^3+ax^2+bx+c$ の両辺を $x$ で微分すると \[\begin{aligned} 2y\frac{dy}{dx} &= 3x^2+2ax+b \\ \frac{dy}{dx} &= \dfrac{3x^2+2ax+b}{2y} \quad (y \neq 0) \end{aligned}\] となるから, $a,$ $b,$ $x_1,$ $y_1$ が有理数であるという仮定により, $E$ の点 $\mathrm P_1$ における接線 $l$ の傾き \[ m = \dfrac{3x_1{}^2+2ax_1+b}{2y_1}\] は有理数である.
- (2)
- 曲線 $E$ の方程式と直線 $l$ の方程式から $y$ を消去すると, \[ x^3+ax^2+bx+c-(mx+n)^2 = 0\] から \[ x^3-(m^2-a)x^2+(b-2mn)x-(n^2-c) = 0\] が得られる. この $3$ 次方程式は $x = x_1,$ $x_2,$ $x_3$ を解にもつから, 解と係数の関係により \[ x_1+x_2+x_3 = m^2-a\] が成り立つ. よって, $a,$ $x_1,$ $x_2,$ $m$ が有理数であることから \[ x_3 = m^2-a-x_1-x_2\] は有理数である. さらに, 直線 $l$ が点 $\mathrm P_3(x_3,y_3)$ を通ることから \[ y_3 = mx_3+n\] であり, $n$ も有理数であるから, $y_3$ も有理数である.
参考
- $y^2 = f(x)$ ($f(x)$: 有理数係数 $3$ 次多項式, $f(x) = 0$ は重解をもたない) の形の方程式で定義される曲線を「数理数体」上の「楕円曲線」(elliptic curve) と呼ぶ. これは, 楕円の周の長さを求める問題を名の由来にもつが, 楕円の周そのものではない.
- $xy$ 平面において $x$ 座標も $y$ 座標も有理数である点を「有理点」(rational point) と呼ぶ.
- 「数理数体」上の「楕円曲線」$E$ について, $\mathrm O$ を「無限遠点」と呼ばれる仮想上の点として,「有理点」$\mathrm P,$ $\mathrm Q$ が与えられたとき, $\mathrm P+\mathrm Q$ を
- $\mathrm P,$ $\mathrm Q$ の $x$ 座標が異なるとき, $E$ と直線 $\mathrm{PQ}$ の交点を $x$ 軸に関して対称移動した点
- $\mathrm P,$ $\mathrm Q$ が異なり, それらの $x$ 座標が等しいとき, $\mathrm O$
- $\mathrm P = \mathrm Q$ であり, その $x$ 座標が $0$ でないとき, $E$ と点 $\mathrm P$ における接線の交点を $x$ 軸に関して対称移動した点
- $\mathrm P = \mathrm Q$ であり, その $x$ 座標が $0$ であるとき, $\mathrm O$
- 「楕円曲線」は, 「フェルマーの最終定理」の証明,「宇宙際タイヒミューラー理論」で利用されるなど, 現代数論で重要な役割を果たす. また, 素因数分解の「楕円曲線法 (レンストラのアルゴリズム)」,「楕円曲線暗号」など, さまざまな応用をもつ.
問題《放物線 $\sqrt x+\sqrt y = 1$ に関する面積の最大値》
曲線 $C:\sqrt x+\sqrt y = 1$ と, $C$ 上の点 $\mathrm P(a,b)$ $(ab \neq 0)$ における $C$ の接線 $\ell$ について, 次の問いに答えよ.
- (1)
- $\ell$ の方程式を求めよ.
- (2)
- $\ell$ と座標軸が囲む三角形の面積 $S$ の最大値を求めよ.
解答例
- (1)
- $x > 0,$ $y > 0$ において $C$ の方程式 $\sqrt x+\sqrt y = 1$ を $x$ で微分すると
$\dfrac{1}{2\sqrt x}+\dfrac{y'}{2\sqrt y} = 0$ つまり $y' = -\dfrac{\sqrt y}{\sqrt x}$となるから, $C$ 上の点 $\mathrm P(a,b)$ における $C$ の接線 $\ell$ の方程式は \[ y = -\frac{\sqrt b}{\sqrt a}(x-a)+b\] である.
- (2)
- $\ell$ と座標軸の交点の座標を $(p,0),$ $(0,q)$ とおくと, \[ 0 = -\frac{\sqrt b}{\sqrt a}(p-a)+b, \quad q = -\frac{\sqrt b}{\sqrt a}(0-a)+b\] から \[ p = a+\sqrt{ab}, \quad q = b+\sqrt{ab}\] となる. また, 点 $\mathrm P$ が曲線 $C$ 上にあることから $\sqrt a+\sqrt b = 1$ が成り立つので, \[ p+q = a+2\sqrt{ab}+b = (\sqrt a+\sqrt b)^2 = 1\] である. よって, $\ell$ と座標軸が囲む三角形の面積は \[\begin{aligned} S &= \frac{1}{2}pq = \frac{1}{2}p(1-p) \\ &= -\frac{1}{2}(p^2-p) = -\frac{1}{2}\left( p-\frac{1}{2}\right) ^2+\frac{1}{8} \end{aligned}\] である. $0 < p < 1$ から, $S$ は $p = \dfrac{1}{2}$ のとき最大値 $\dfrac{1}{8}$ をとる. ($S$ の最大値を与える点 $\mathrm P$ の座標は $\left(\dfrac{1}{4},\dfrac{1}{4}\right)$ である.)
法線
定理《関数のグラフの法線》
$x = \alpha$ において微分可能な関数 $f(x)$ のグラフ $y = f(x)$ の点 $(\alpha ,f(\alpha ))$ における法線の方程式は,
$f'(\alpha ) \neq 0$ のとき $y-f(\alpha ) = -\dfrac{1}{f'(\alpha )}(x-\alpha ),$
$f'(\alpha ) = 0$ のとき $x = \alpha$
である.
$f'(\alpha ) \neq 0$ のとき $y-f(\alpha ) = -\dfrac{1}{f'(\alpha )}(x-\alpha ),$
$f'(\alpha ) = 0$ のとき $x = \alpha$
である.
問題《放物線の縮閉線》
放物線 $y = x^2$ の点 $(a,a^2),$ $(a+t,(a+t)^2)$ $(t,\ a+t \neq 0)$ における $2$ 本の法線の交点を $(x(t),y(t))$ とおき, $p = \lim\limits_{t \to 0}x(t),$ $q = \lim\limits_{t \to 0}y(t)$ とおく.
- (1)
- $p,$ $q$ の値を求めよ.
- (2)
- $2$ 点 $(a,a^2),$ $(p,q)$ の間の距離 $r$ を求めよ.
- (3)
- $a$ が実数全体を動くとき, 点 $(p,q)$ の軌跡を求めよ.
解答例
- (1)
- 放物線 $y = x^2$ の点 $(a,a^2)$ における法線の方程式は,
$a = 0$ のとき $x = 0$ であり, $a \neq 0$ のとき
である. また, $y = x^2$ の点 $(a+t,(a+t)^2)$ における法線の方程式は, $a+t \neq 0$ のとき \[ y = -\frac{1}{2(a+t)}x+(a+t)^2+\frac{1}{2}\] である.
$y-a^2 = -\dfrac{1}{2a}(x-a)$ つまり $y = -\dfrac{1}{2a}x+a^2+\dfrac{1}{2}$ - (i)
- $a = 0$ のとき. $2$ 本の法線 $x = 0,$ $y = -\dfrac{1}{2t}x+t^2+\dfrac{1}{2}$ の交点の $x$ 座標は $x(t) = 0,$ $y$ 座標は $y(t) = t^2+\dfrac{1}{2}$ であるから, $t \to 0$ とすると \[ p = 0, \quad q = \frac{1}{2}\] が得られる.
- (ii)
- $a \neq 0$ のとき. $2$ 本の法線の交点の $x$ 座標は \[ -\frac{1}{2a}x+a^2+\frac{1}{2} = -\frac{1}{2(a+t)}x+(a+t)^2+\frac{1}{2}\] の解 \[ x(t) = -2a(a+t)(2a+t)\] であり, $y$ 座標は \[ y(t) = -\frac{1}{2a}x(t)+a^2+\frac{1}{2}\] であるから, $t \to 0$ とすると \[\begin{aligned} p &= -4a^3, \\ q &= -\frac{1}{2a}p+a^2+\frac{1}{2} = 3a^2+\frac{1}{2} \end{aligned}\] が得られる.
- (2)
- $[1],$ $[2]$ から, $2$ 点 $(a,a^2),$ $(p,q)$ の間の距離は \[ r = \sqrt{(-4a^3-a)^2+\left( 2a^2+\frac{1}{2}\right) ^2} = \frac{(1+4a^2)^{\frac{3}{2}}}{2}\] である.
- (3)
- $[1],$ $[2]$ から $a$ を消去すると, \[ q = \frac{3}{\sqrt[3]{16}}p^{\frac{2}{3}}+\frac{1}{2}\] となる. よって, 求める軌跡は曲線 \[ y = \frac{3}{\sqrt[3]{16}}x^{\frac{2}{3}}+\dfrac{1}{2}\] である.
参考
- 本問において, 点 $(p,q)$ を中心とする半径 $r$ の円周は点 $(a,a^2)$ において放物線 $y = x^2$ をよく近似している.
このような円を「曲率円」(curvature circle) と呼び, その半径 $r$ を「曲率半径」(radius of curvature), $\dfrac{1}{r}$ を「曲率」(curvature)と呼ぶ (厳密な定義は省略).
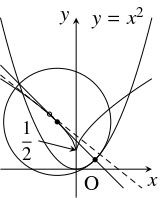
- $2$ 階微分可能な関数 $y = f(x)$ のグラフの点 $(a,f(a))$ における「曲率半径」$r$ は, $f''(a) \neq 0$ のとき \[ r = \frac{\{ 1+f'(a)^2\} ^{\frac{3}{2}}}{|f''(a)|}\] であることが知られている.
- 曲線の「曲率円」の中心の軌跡を「縮閉線」(evolute) と呼ぶ.
問題《初等超越関数のグラフの曲率半径》
次の関数 $f(x)$ のグラフ $C:y = f(x)$ 上の異なる $2$ 点 $(a,f(a)),$ $(t,f(t))$ における法線の交点 $(u(t),v(t))$ について,
$p = \lim\limits_{t \to a}u(t),$ $q = \lim\limits_{t \to a}v(t)$ とおく.
$a$ が $f(x)$ の定義域全体を動くとき, $2$ 点 $(a,f(a)),$ $(p,q)$ を結ぶ線分の長さ $r(a)$ の最小値を求めよ.
- (A)
- $f(x) = e^x$
- (B)
- $f(x) = \cos x$ $\left( -\dfrac{\pi}{2} < x < \dfrac{\pi}{2}\right)$
- (C)
- $f(x) = \tan x$ $\left( 0 < x < \dfrac{\pi}{2}\right)$
解答例
- (A)
- $f'(x) = e^x$ であるから, $C:y = f(x)$ の点 $(a,f(a)),$ $(t,f(t))$ における法線の方程式はそれぞれ \[ y = -e^{-a}(x-a)+e^a, \quad y = -e^{-t}(x-t)+e^t\] である. これらの交点の $x$ 座標は \[\begin{aligned} -e^{-a}(x-a)+e^a &= -e^{-t}(x-t)+e^t \\ e^t(x-a)-e^{t+2a} &= e^a(x-t)-e^{2t+a} \\ (e^t-e^a)x &= ae^t-te^a-e^{t+a}(e^t-e^a) \end{aligned}\] の解であるから, \[\begin{aligned} u(t) &= \frac{a(e^t-e^a)-(t-a)e^a}{e^t-e^a}-e^{t+a} \\ &= a-e^a\cdot\frac{t-a}{e^t-e^a}-e^{t+a} \end{aligned}\] である. よって, $t \to a$ とすると \[\begin{aligned} p &= a-e^a\cdot\frac{1}{(e^x)'|_{x = a}}-e^{2a} \\ &= a-e^a\cdot\frac{1}{e^a}-e^{2a} = a-e^{2a}-1, \\ q &= -e^{-a}(p-a)+e^a \\ &= -e^{-a}(-e^{2a}-1)+e^a = 2e^a+e^{-a} \end{aligned}\] が得られるから, \[\begin{aligned} r(a)^2 &= (-e^{2a}-1)^2+(e^a+e^{-a})^2 \\ &= (e^{2a}+1)^2+e^{-2a}(e^{2a}+1)^2 = \frac{(e^{2a}+1)^3}{e^{2a}} \end{aligned}\] である. $b = e^{2a}\,(b > 0)$ とおく. このとき, \[\begin{aligned} r(a)^2 &= \dfrac{(b+1)^3}{b}, \\ \frac{d}{db}r(a)^2 &= \frac{(b+1)^2(2b-1)}{b^2} \end{aligned}\] となるから, $r(a)^2$ は $b = \dfrac{1}{2}$ つまり $a = -\dfrac{1}{2}\log 2$ のとき最小値 $\left(\dfrac{1}{2}+1\right) ^3\div\dfrac{1}{2} = \dfrac{27}{4}$ をとる. $r(a) > 0$ であるから, $r(a)$ は $a = -\dfrac{1}{2}\log 2$ のとき極小かつ最小の値 $\dfrac{3\sqrt 3}{2}$ をとる.
- (B)
- $f'(x) = -\sin x$ であるから, $C:y = f(x)$ の点 $(a,f(a)),$ $(t,f(t))$ における法線の方程式はそれぞれ \[ y = \frac{1}{\sin a}(x-a)+\cos a, \quad y = \frac{1}{\sin t}(x-t)+\cos t\] である. これらの交点の $x$ 座標は \[\begin{aligned} &\frac{1}{\sin a}(x-a)+\cos a = \frac{1}{\sin t}(x-t)+\cos t \\ &(\sin t\!-\!\sin a)x = a\sin t\!-\!t\sin a\!+\!\sin a\sin t(\cos t\!-\!\cos a) \end{aligned}\] の解であるから, \[\begin{aligned} u(t) &= \frac{a(\sin\!t\!-\!\sin\!a)\!-\!(t\!-\!a)\sin\!a\!+\!\sin\!a\!\sin\!t(\cos\!t\!-\!\cos\!a)}{\sin\!t-\sin\!a} \\ &= a-\frac{\sin a-\sin a\sin t\cdot\dfrac{\cos t-\cos a}{t-a}}{\dfrac{\sin t-\sin a}{t-a}} \end{aligned}\] である. よって, $t \to a$ とすると \[\begin{aligned} p &= a-\frac{\sin a-\sin ^2a\cdot (\cos x)'|_{x = a}}{(\sin x)'|_{x = a}} \\ &= a-\frac{\sin a+\sin ^3a}{\cos a} = a-\tan a(1+\sin ^2a), \\ q &= \frac{1}{\sin a}(p-a)+\cos a \\ &= \frac{1}{\sin a}(-\tan a)(1\!+\!\sin ^2a)\!+\!\cos a = \cos a\!-\!\frac{1\!+\!\sin ^2a}{\cos a} \end{aligned}\] が得られるから, \[\begin{aligned} r(a)^2 &= \{ -\tan a(1+\sin ^2a)\} ^2+\left( -\frac{1+\sin ^2a}{\cos a}\right) ^2 \\ &= \frac{(1+\sin ^2a)^3}{\cos ^2a} = \frac{(2-\cos ^2a)^3}{\cos ^2a} \end{aligned}\] である. $b = \cos ^2a\,(0 < b \leqq 1)$ とおく. このとき, \[\begin{aligned} r(a)^2 &= \dfrac{(2-b)^3}{b}, \\ \frac{d}{db}r(a)^2 &= -\frac{2(2-b)^2(1+b)}{b^2} < 0 \end{aligned}\] となるから, $r(a)^2$ は $b = 1$ つまり $a = 0$ のとき最小値 $1$ をとる. $r(a) > 0$ であるから, $r(a)$ は $a = 0$ のとき最小値 $1$ をとる.
- (C)
- $f'(x) = \dfrac{1}{\cos ^2x}$ であるから, $C:y = f(x)$ の点 $(a,f(a)),$ $(t,f(t))$ における法線の方程式はそれぞれ \[ y = -\cos ^2a(x\!-\!a)\!+\!\tan a, \quad y = -\cos ^2t(x\!-\!t)\!+\!\tan t\] である. これらの交点の $x$ 座標は \[\begin{aligned} &-\cos ^2a(x-a)+\tan a = -\cos ^2t(x-t)+\tan t \\ &(\cos ^2t-\cos ^2a)x = t\cos ^2t-a\cos ^2a+\tan t-\tan a \end{aligned}\] の解であるから, \[\begin{aligned} u(t) &= \frac{t\cos ^2t-a\cos ^2a+\tan t-\tan a}{\cos ^2t-\cos ^2a} \\ &= \frac{\dfrac{t\cos ^2t-a\cos ^2a}{t-a}+\dfrac{\tan t-\tan a}{t-a}}{\dfrac{\cos ^2t-\cos ^2a}{t-a}} \end{aligned}\] である. よって, $t \to a$ とすると \[\begin{aligned} p &= \frac{(x\cos ^2x)'|_{x = a}+(\tan x)'|_{x = a}}{(\cos ^2x)'|_{x = a}} \\ &= \frac{\cos ^2a-2a\sin a\cos a+\dfrac{1}{\cos ^2a}}{-2a\sin a\cos a} = a-\frac{1+\cos ^4a}{2\sin a\cos ^3a}, \\ q &= -\cos ^2a(p-a)+\tan a \\ &= -\!\cos ^2\!a\!\left(\!-\frac{1\!+\!\cos ^4\!a}{2\sin\!a\cos ^3\!a}\!\right)\!+\!\tan\!a = \tan\!a\!+\!\frac{1\!+\!\cos ^4\!a}{2\sin\!a\cos\!a} \end{aligned}\] が得られるから, \[\begin{aligned} r(a)^2 &= \left( -\frac{1+\cos ^4a}{2\sin a\cos ^3a}\right) ^2+\left(\frac{1+\cos ^4a}{2\sin a\cos a}\right) ^2 \\ &= \frac{(1+\cos ^4a)^3}{4\sin ^2a\cos ^6a} = \frac{(1+\cos ^4a)^3}{4\cos ^6a(1-\cos ^2a)} \end{aligned}\] である. $b = \cos ^2a\,(0 < b < 1)$ とおく. このとき, \[\begin{aligned} r(a)^2 &= \frac{(1+b^2)^3}{4b^3(1-b)}, \\ \frac{d}{db}r(a)^2 &= -\frac{(1+b^2)^2(2b^3-3b^2-4b+3)}{4b^4(1-b)^2} \end{aligned}\] となる. \[\begin{aligned} 2\cdot (-2)^3-3\cdot (-2)^2-4\cdot (-2)+3 &= -17 < 0, \\ 2\cdot 0^3-3\cdot 0^2-4\cdot 0+3 &= 3 > 0, \\ 2\cdot 1^3-3\cdot 1^2-4\cdot 1+3 &= -2 < 0, \\ 2\cdot 3^3-3\cdot 3^2-4\cdot 3+3 &= 18 > 0 \end{aligned}\] であるから, 中間値の定理により $2b^3-3b^2-4b+3 = 0$ は $0 < b < 1$ の範囲にただ $1$ つの解 $b = b_0$ をもち, $2b^3-3b^2-4b+3$ は $b < b_0$ のとき正, $b > b_0$ のとき負である. よって, $r(a)^2$ は $b = b_0$ のとき極小かつ最小の値 $\dfrac{(1+b_0{}^2)^3}{4b_0{}^3(1-b_0)}$ をとる. $r(a) > 0$ であるから, $r(a)$ は最小値 $\sqrt{\dfrac{(1+b_0{}^2)^3}{4b_0{}^3(1-b_0)}}$ をとる.
参考
対数関数 $y = \log x$ のグラフの「曲率半径」は点 $\left( -\dfrac{1}{2}\log 2,\dfrac{1}{\sqrt 2}\right)$ において最小値 $\dfrac{3\sqrt 3}{2}$ をとる.
