解と係数の関係
解と係数の関係
定理《方程式の解と係数の関係》
$a,$ $b,$ $c,$ $d$ $(a \neq 0)$ を複素数とする.
- (1)
- $2$ 次方程式 $ax^2+bx+c = 0$ の $2$ 解が $\alpha,$ $\beta$ であるためには, \[\alpha +\beta = -\frac{b}{a}, \quad \alpha\beta = \frac{c}{a}\] の成り立つことが必要十分である.
- (2)
- $3$ 次方程式 $ax^3+bx^2+cx+d = 0$ の $3$ 解が $\alpha,$ $\beta,$ $\gamma$ であるためには, \[\alpha +\beta +\gamma =-\frac{b}{a},\ \alpha\beta +\beta\gamma +\gamma\alpha = \frac{c}{a},\ \alpha\beta\gamma = -\frac{d}{a}\] の成り立つことが必要十分である.
証明
$a(x-\alpha )(x-\beta ),$ $a(x-\alpha )(x-\beta )(x-\gamma )$ を展開して係数を比較することによりわかる (解の公式を使う必要はない).
問題《$2$ 次方程式の解の公式》
$2$ 次方程式 $ax^2+bx+c = 0$ ($a,$ $b,$ $c$: 定数, $a > 0$) の解の公式を, 解と係数の関係を利用して導け.
解答例
$2$ 次方程式 $ax^2+bx+c = 0\ \cdots [*]$ の $2$ 解を $\alpha,$ $\beta$ $(\alpha \geqq \beta )$ とおく.
解と係数の関係により,
\[\alpha +\beta = -\frac{b}{a}\ \cdots [1], \quad \alpha\beta = \frac{c}{a}\]
が成り立つ.
よって,
\[\begin{aligned}
\alpha -\beta &= \sqrt{(\alpha +\beta )^2-4\alpha\beta} \\
&= \sqrt{\left( -\frac{b}{a}\right) ^2-4\cdot\frac{c}{a}} = \sqrt{\frac{b^2-4ac}{a^2}} \\
&= \frac{\sqrt{b^2-4ac}}{a} \quad \cdots [2]
\end{aligned}\]
であるので, $([1]+[2])\div 2,$ $([1]-[2])\div 2$ から,
\[\alpha = \frac{-b+\sqrt{b^2-4ac}}{2a}, \quad \beta = \frac{-b-\sqrt{b^2-4ac}}{2a}\]
が得られる.
よって, $[*]$ の解は $x = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$ である.
問題《一般リュカ数列の恒等式》
整数係数 $2$ 次方程式 $x^2-px+q = 0$ が実数解 $\alpha,$ $\beta$ $(\alpha > \beta )$ をもつとし, 各正の整数 $n$ に対して
\[ x_n = \alpha ^n+\beta ^n, \quad y_n = \frac{\alpha ^n-\beta ^n}{\alpha -\beta}\]
と定める.
また, $D = p^2-4q$ とおく.
- (1)
- $p,$ $q$ を用いて $\alpha +\beta,$ $\alpha\beta,$ $\alpha -\beta$ を表せ.
- (2)
- 等式 \[\begin{aligned} x_1 &= p, & x_2 &= p^2-2q, & x_{n+2} &= px_{n+1}-qx_n \\ y_1 &= 1, & y_2 &= p, & y_{n+2} &= py_{n+1}-qy_n \end{aligned}\] が成り立つことを示せ.
- (3)
- 等式 \[ x_n{}^2-Dy_n{}^2 = 4q^n\] が成り立つことを示せ.
解答例
- (1)
- 解と係数の関係により \[\alpha +\beta = p \quad \cdots [1], \qquad \alpha\beta = q \quad \cdots [2]\] であるから, \[ (\alpha -\beta )^2 = (\alpha +\beta )^2-4\alpha\beta = p^2-4q\] が成り立つ. また, $2$ 次方程式 $x^2-px+q = 0$ が異なる $2$ つの実数解をもつことから $p^2-4q > 0$ であるので, \[\alpha -\beta = \sqrt{p^2-4q} \quad \cdots [3]\] が成り立つ.
- (2)
- 定義と $[1],$ $[2]$ により \[\begin{aligned} x_1 &= \alpha +\beta = p, \\ x_2 &= \alpha ^2+\beta ^2 = (\alpha +\beta )^2-2\alpha\beta = p^2-2q, \\ y_1 &= \frac{\alpha -\beta}{\alpha -\beta} = 1, \\ y_2 &= \dfrac{\alpha ^2-\beta ^2}{\alpha -\beta} = \alpha +\beta = p \end{aligned}\] であり, \[\begin{aligned} \alpha ^{n+2}+\beta ^{n+2} &= (\alpha ^{n+1}+\beta ^{n+1})(\alpha +\beta )-\alpha\beta (\alpha ^n+\beta ^n), \\ \alpha ^{n+2}-\beta ^{n+2} &= (\alpha ^{n+1}-\beta ^{n+1})(\alpha +\beta )-\alpha\beta (\alpha ^n-\beta ^n) \end{aligned}\] であるから \[ x_{n+2} = px_{n+1}-qx_n, \quad y_{n+2} = py_{n+1}-qy_n\] が成り立つ.
- (3)
- $[3]$ により $y_n\sqrt D = y_n(\alpha -\beta ) = \alpha ^n-\beta ^n$ であるから, \[\begin{aligned} &x_n{}^2-Dy_n{}^2 = (x_n+y_n\sqrt D)(x_n-y_n\sqrt D) \\ &= \{ (\alpha ^n+\beta ^n)+(\alpha ^n-\beta ^n)\}\{ (\alpha ^n+\beta ^n)-(\alpha ^n-\beta ^n)\} \\ &= 2\alpha ^n\cdot 2\beta ^n = 4(\alpha\beta )^n = 4q^n \end{aligned}\] が成り立つ.
参考
- 上記のように定まる数列 $\{ x_n\},$ $\{ y_n\}$ は「一般リュカ数列」(generalized Lucas sequence) と呼ばれる. (2) の初期値, 漸化式で定義しても同じ数列が得られる.
- $p$ が偶数のとき, $x_n$ は常に偶数である.
- $p = 1,$ $q = -1$ のとき, $\{ x_n\}$ は「リュカ数列」(Lucas sequence), $\{ y_n\}$ は「フィボナッチ数列」(Fibonacci sequence) として知られている (こちらを参照).
- $p = 2,$ $q = -1$ のとき, $\{ x_n\}$ は「同伴ペル数列」(companion Pell sequence), $\{ y_n\}$ は「ペル数列」(Pell sequence) として知られており, $x_n{}^2-8y_n{}^2 = 4(-1)^n$ が成り立つ. $x_n = 2h_n$ とおくと, $h_n{}^2-2y_n{}^2 = (-1)^n$ が成り立つ. つまり, $(x,y) = (h_n,y_n)$ は「ペル方程式」(Pell's equation) $|x^2-2y^2| = 1$ を満たす (こちらを参照).
問題《掛谷流の $2$ 次方程式の解の評価》
$a,$ $b,$ $c$ を $a > b > c > 0$ なる実数とし, $\alpha$ を $2$ 次方程式 $ax^2+bx+c = 0$ の解とする.
このとき, $|\alpha | < 1$ であることを, 次の場合に分けて示せ.
- (i)
- $\alpha$ が実数であるとき.
- (ii)
- $\alpha$ が虚数であるとき.
解答例
$ax^2+bx+c = 0$ のもう $1$ つの解を $\beta$ とおく.
解と係数の関係により
\[\alpha +\beta = -\frac{b}{a} \quad \cdots [1], \quad \alpha\beta = \frac{c}{a} \quad \cdots [2]\]
が成り立つ.
- (i)
- $\alpha$ が実数であるとき. $\beta$ も実数である. $[1],$ $[2]$ と $a,$ $b,$ $c > 0$ から $\alpha+\beta < 0,$ $\alpha\beta > 0$ であり, よって $\alpha,$ $\beta < 0$ である. したがって, $a > b$ から \[ |\alpha | < |\alpha |+|\beta | = |\alpha +\beta | = \frac{b}{a} < 1\] が成り立ち, $|\alpha | < 1$ が得られる.
- (ii)
- $\alpha$ が虚数であるとき. $\beta = \bar\alpha$ であるので, $[2]$ と $a > c$ から \[ |\alpha |^2 = \alpha\bar\alpha = \alpha\beta = \frac{c}{a} < 1\] が成り立ち, $|\alpha | < 1$ が得られる.
参考
一般に, $a_n > \cdots > a_1 > a_0 > 0$ のとき,
$n$ 次方程式 $a_nx^n+\cdots +a_1x+a_0 = 0$ の解 $\alpha$ の絶対値は $1$ 未満であることが「エネストレーム=掛谷の定理」(Eneström–Kakeya Theorem) として知られている.
問題《$2$ 次体の整数環》
$d$ を $1$ 以外の平方数で割り切れない整数とする.
$\mathbb Q$ を有理数全体の集合とし, 集合 $K$ を
\[ K = \{ a_1+a_2\sqrt d \mid a_1,\ a_2 \in \mathbb Q\}\]
で定める.
$\alpha = a_1+a_2\sqrt d \in K$ $(a_1,\ a_2 \in \mathbb Q)$ のとき,
\[\begin{aligned}
\tilde\alpha &= a_1-a_2\sqrt d, \\
T(\alpha ) &= \alpha +\tilde\alpha = 2a_1, \\
N(\alpha ) &= \alpha\tilde\alpha = a_1{}^2-da_2{}^2
\end{aligned}\]
とおく.
また, $\mathbb Z$ を整数全体の集合とし, 集合 $O$ を $K$ の要素のうち最高次の係数が $1$ である $2$ 次以下の整数係数方程式の解であるもの全体とする.
次のことを示せ.
偶数, 奇数の $2$ 乗を $4$ で割った余りがそれぞれ $0,$ $1$ であること, 有理数 $x$ に対して $dx^2 \in \mathbb Z \Longrightarrow x \in \mathbb Z$ が成り立つこと(こちらを参照) は, 証明なしに用いてよい.
- (1)
- \[ O = \{\alpha \in K \mid T(\alpha ),\ N(\alpha ) \in \mathbb Z\} \quad \cdots [\ast ]\] である.
- (2)
- $d \equiv 2,\ 3 \pmod 4$ のとき, \[ O = \{ a_1+a_2\sqrt d \mid a_1,\ a_2 \in \mathbb Z\} \quad \cdots [\ast ]'\] である.
- (3)
- $d \equiv 1 \pmod 4$ のとき, \[ O = \left\{\frac{a_1+a_2\sqrt d}{2} \mid a_1,\ a_2 \in \mathbb Z,\ a_1 \equiv a_2\ (\text{mod}\ 2)\right\} \quad \cdots [\ast ]''\] である.
解答例
- (1)
- $\alpha = a_1+a_2\sqrt d \in K$ とする.
- (i)
- $a_2 = 0$ のとき. $\alpha$ は有理数であり, $1$ 次方程式 $x-\alpha = 0$ の解であるから, \[\begin{aligned} \alpha \in O &\iff \alpha \in \mathbb Z \\ &\iff T(\alpha ) = 2\alpha,\ N(\alpha ) = \alpha ^2 \in \mathbb Z \end{aligned}\] が成り立つ.
- (ii)
- $a_2 \neq 0$ のとき. $\alpha$ は無理数である. $\alpha = a_1+a_2\sqrt d$ を解にもつ有理数係数 $2$ 次方程式は $\tilde\alpha = a_1-a_2\sqrt d$ も解にもつから, $\alpha$ を解にもつ $2$ 次方程式の $1$ つは \[\begin{aligned} (x-\alpha )(x-\tilde\alpha ) &= 0 \\ x^2-(\alpha +\tilde\alpha )x+\alpha\tilde\alpha &= 0 \\ x^2-T(\alpha )x+N(\alpha ) &= 0 \end{aligned}\] である. よって, \[\alpha \in O \iff T(\alpha ),\ N(\alpha ) \in \mathbb Z\] が成り立つ.
- (2)
- $d \equiv 2,\ 3 \pmod 4$ とする.
$[\ast ]'$ の右辺を $O'$ とおく.
- $O' \subset O$ は, $a_1,$ $a_2 \in \mathbb Z$ のとき \[\begin{aligned} T(a_1+a_2\sqrt d) &= 2a_1 \in \mathbb Z, \\ N(a_1+a_2\sqrt d) &= a_1{}^2-da_2{}^2 \in \mathbb Z \end{aligned}\] であることから従う.
- $O \subset O'$ を示すため, $\alpha = a_1+a_2\sqrt d \in O$ $(a_1,\ a_2 \in \mathbb Q)$ とする.
このとき, (1) により, $T(\alpha ) = 2a_1,$ $N(\alpha ) = a_1{}^2-da_2{}^2$ は整数である.
よって,
\[ 4N(\alpha ) = (2a_1)^2-d(2a_2)^2\]
は整数であるから, $d(2a_2)^2$ は整数, したがって $2a_2$ は整数である.
そこで, $b_1 = 2a_1,$ $b_2 = 2a_2$ とおく.
このとき,
\[ a_1{}^2-da_2{}^2 = \frac{b_1{}^2-db_2{}^2}{4}\]
は整数であるから, $b_1{}^2-db_2{}^2$ は $4$ の倍数である.
- (i)
- $b_1$ が偶数, $b_2$ が奇数のとき. \[ b_1{}^2-db_2{}^2 \equiv -d \equiv 1,\ 2 \not\equiv 0 \pmod 4\] となって矛盾.
- (ii)
- $b_1$ が奇数, $b_2$ が偶数のとき. \[ b_1{}^2-db_2{}^2 \equiv 1 \not\equiv 0 \pmod 4\] となって矛盾.
- (iii)
- $b_1$ が奇数, $b_2$ が奇数のとき. \[ b_1{}^2-db_2{}^2 \equiv 1-d \equiv 2,\ 3 \not\equiv 0 \pmod 4\] となって矛盾.
- (3)
- $d \equiv 1 \pmod 4$ とする.
$[\ast ]''$ の右辺を $O''$ とおく.
- $O'' \subset O$ は, $a_1,$ $a_2 \in \mathbb Z,$ $a_1 \equiv a_2\ (\text{mod}\ 2)$ のとき \[\begin{aligned} T\left(\frac{a_1+a_2\sqrt d}{2}\right) &= a_1 \in \mathbb Z, \\ N\left(\frac{a_1+a_2\sqrt d}{2}\right) &= \frac{a_1{}^2-da_2{}^2}{4} \in \mathbb Z \end{aligned}\] であることから従う. ここで, \[\begin{aligned} a_1{}^2-da_2{}^2 &\equiv a_1{}^2-a_2{}^2 \equiv \begin{cases} 0-0 & (a_1 \equiv a_2 \equiv 0\ (\text{mod}\ 2)), \\ 1-1 & (a_1 \equiv a_2 \equiv 1\ (\text{mod}\ 2)) \end{cases} \\ &\equiv 0 \pmod 4 \end{aligned}\] であることに注意する.
- $O \subset O''$ を示すため, $\alpha = x_1+x_2\sqrt d \in O$ $(x_1,\ x_2 \in \mathbb Q)$ とする.
このとき, (1) により, $T(\alpha ) = 2x_1,$ $N(\alpha ) = x_1{}^2-dx_2{}^2$ は整数である.
よって,
\[ 4N(\alpha ) = (2x_1)^2-d(2x_2)^2\]
は整数であるから, $d(2x_2)^2$ は整数, したがって $2x_2$ は整数である.
そこで, $2x_1 = a_1,$ $2x_2 = a_2$ とおく.
このとき,
\[ x_1{}^2-dx_2{}^2 = \frac{a_1{}^2-da_2{}^2}{4}\]
は整数であるから, $a_1{}^2-da_2{}^2$ は $4$ の倍数である.
- (i)
- $a_1$ が偶数, $a_2$ が奇数のとき. \[ a_1{}^2-da_2{}^2 \equiv 0-1\cdot 1 \equiv 3 \not\equiv 0 \pmod 4\] となって矛盾.
- (ii)
- $a_1$ が奇数, $a_2$ が偶数のとき. \[ a_1{}^2-da_2{}^2 \equiv 1-1\cdot 0 = 1 \not\equiv 0 \pmod 4\] となって矛盾.
参考
- 四則演算が定義され, 交換法則, 結合法則, 分配法則を満たす数の集合で, 複数の要素をもつものを「
体 」(field) と呼ぶ. 例えば, 有理数全体 $\mathbb Q$ は通常の四則演算に関して「体」をなす. これを「有理数体」(field of rational numbers) と呼ぶ. 現代数学において, 方程式論は「体」の理論,「体論」として展開されている. - 平方数でない整数 $d$ に対して, $\mathbb Q$ と $x^2 = d$ の解 $x = \pm\sqrt d$ を含む最小の「体」は $K = \{ a_1+a_2\sqrt d \mid a_1,a_2 \in \mathbb Q\}$ であることが知られている. この形の「体」を「$2$ 次体」(quadratic field) と呼ぶ. 関数 $T(\alpha ),$ $N(\alpha )$ $(\alpha \in K)$ はそれぞれ「トレース写像」(trace map), 「ノルム写像」(norm map) と呼ばれる.
- 「$2$ 次体」のように,「体」$K$ の要素を係数とする多項式 $f(x)$ に対して, $K$ と方程式 $f(x) = 0$ の解を含む最小の「体」を $f(x)$ の $K$ 上の「最小分解体」(smallest splitting field) と呼ぶ. ある有理数係数多項式の $\mathbb Q$ 上の「最小分解体」を「代数体」(algebraic field) と呼ぶ.
- 最高次の係数が $1$ のある整数係数多項式 $f(x)$ について, $f(x) = 0$ の解になる複素数は「代数的整数」(algebraic integer) と呼ばれる. 「代数体」$K$ に属する「代数的整数」全体は $K$ の「整数環」(ring of integers) と呼ばれる (こちらも参照).
問題《マルコフの $3$ つ組とその類似》
- (A)
- $x,$ $y,$ $z$ の方程式
\[ x^2+y^2+z^2 = 3xyz \quad (x,\ y \leqq z) \quad \cdots [*]\]
について, 次の問いに答えよ.
- (1)
- $[*]$ の正の整数解を $1$ つ求めよ.
- (2)
- $(x,y,z) = (a,b,c)$ を $[*]$ の正の整数解とする. このとき, $(x,y,z) = (b,c,d)$ が $[*]$ の正の整数解になるような整数 $d$ が存在することを示せ.
- (3)
- $[*]$ の正の整数解は無限に存在することを示せ.
(参考: $2006$ 東京大) - (B)
- $x,$ $y,$ $z$ の方程式
\[\begin{aligned}
(x+y)^2+(y+z)^2+(z+x)^2 = 12xyz \quad (x,\ y &\leqq z) \\
&\cdots [*]
\end{aligned}\]
について, 次の問いに答えよ.
- (1)
- $[*]$ の正の整数解を $1$ つ求めよ.
- (2)
- $(x,y,z) = (a,b,c)$ を $[*]$ の正の整数解とする. このとき, $(x,y,z) = (b,c,d)$ が $[*]$ の正の整数解になるような整数 $d$ が存在することを示せ.
- (3)
- $[*]$ の正の整数解は無限に存在することを示せ.
(参考: Y. Gyoda, “Positive integer solutions to
$(x+y)^2+(y+z)^2+(z+x)^2 = 12xyz$,” $2021$)
解答例
- (A)
- (1)
- $(x,y,z) = (1,1,1)$ は $[*]$ の正の整数解である.
- (2)
- $x$ の $2$ 次方程式 \[ x^2+b^2+c^2 = 3xbc\] つまり \[ x^2-3bcx+b^2+c^2 = 0\] は解 $x = a$ をもつ. よって, この $2$ 次方程式のもう $1$ つの解 $x = d$ は, 解と係数の関係により \[ a+d = 3bc\] を満たし, \[ d = 3bc-a\] と表される. また, \[\begin{aligned} d-c &= (3bc-a)-c \\ &= (3b-1)c-a \\ &\geqq 2c-a \quad (\because b \geqq 1)\\ &> 0 \quad (\because c \geqq a) \end{aligned}\] から $0 < b \leqq c < d$ であるので, $(x,y,z) = (b,c,3bc-a)$ は $[*]$ の正の整数解である.
- (3)
- 数列 $\{ x_n\},$ $\{ y_n\},$ $\{ z_n\}$ を初期条件 $x_1 = y_1 = z_1 = 1$ と連立漸化式 \[\begin{cases} x_{n+1} = y_n, \\ y_{n+1} = z_n, \\ z_{n+1} = 3y_nz_n-x_n \end{cases}\] で定めると, $z_n < z_{n+1}$ となるから, 無限に多くの, $[*]$ の正の整数解 $(x,y,z) = (x_n,y_n,z_n)$ $(n \geqq 1)$ が得られる.
- (B)
- (1)
- $(x,y,z) = (1,1,1)$ は $[*]$ の正の整数解である.
- (2)
- $x$ の $2$ 次方程式 \[ (x+b)^2+(b+c)^2+(c+x)^2 = 12xbc\] つまり \[ x^2-(6bc-b-c)x+b^2+bc+c^2 = 0\] は解 $x = a$ をもつ. よって, この $2$ 次方程式のもう $1$ つの解 $x = d$ は, 解と係数の関係により \[ a+d = 6bc-b-c\] を満たし, \[ d = 6bc-a-b-c\] と表される. また, \[\begin{aligned} d-c &= (6bc-a-b-c)-c \\ &= (3b-1)2c-a-b \\ &\geqq 2\cdot 2sc-a-b \quad (\because b \geqq 1)\\ &= (2c-a)+(2c-b) \\ &> 0 \quad (\because c \geqq a,\ b) \end{aligned}\] から $0 < b \leqq c < d$ であるので, $(x,y,z) = (b,c,6bc-a-b-c)$ は $[*]$ の正の整数解である.
- (3)
- 数列 $\{ x_n\},$ $\{ y_n\},$ $\{ z_n\}$ を初期条件 $x_1 = y_1 = z_1 = 1$ と連立漸化式 \[\begin{cases} x_{n+1} = y_n, \\ y_{n+1} = z_n, \\ z_{n+1} = 6y_nz_n-x_n-y_n-z_n \end{cases}\] で定めると, $z_n < z_{n+1}$ となるから, 無限に多くの, $[*]$ の正の整数解 $(x,y,z) = (x_n,y_n,z_n)$ $(n \geqq 1)$ が得られる.
参考
- (A) の方程式 $x^2+y^2+z^2 = 3xyz$ を「マルコフ方程式」(Markov equation) と呼び, その正の整数解を「マルコフの $3$ つ組」(Markov triple) と呼ぶ.
すべての「マルコフの $3$ つ組」は, $(1,1,1)$ から, $x,y,z$ の置換と $(x,y,z)$ を $(y,z,3yz-x)$ に対応させる変換の組合せにより構成できることが知られており, $x \leqq y \leqq z$ とすると次のような図にまとめられる.
この図を「マルコフ木」(Markov tree) と呼ぶ.
ここで, $(x,y,z)$ を $(x,z,3xz-y)$ または $(y,z,3yz-x)$ に変換すると $z$ の値は大きくなり, $(3xy-z,x,y)$ に変換して必要に応じて並べ替えると $z$ の値は小さくなる.
「マルコフの $3$ つ組」$(x,y,z)$ $(x \leqq y \leqq z)$ において, $z$ の値はすべて異なるという予想がある.
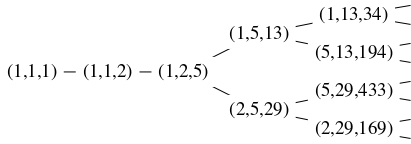
- $\{ F_n\}$ を「フィボナッチ数列」(こちらを参照), $\{ P_n\}$ を「ペル数列」(こちらを参照) とする. すべての正の整数 $n$ に対して, \[ (1,F_{2n-1},F_{2n+1}), \quad (2,P_{2n-1},P_{2n+1})\] は「マルコフの $3$ つ組」である. 実際, \[ (1,F_1,F_3) = (1,1,2), \quad (2,P_1,P_3) = (2,1,5)\] は「マルコフの $3$ つ組」であり, $(x,y,z) = (1,F_{2n-1},F_{2n+1}),$ $(2,P_{2n-1},P_{2n+1})$ ($n$: 正の整数) が「マルコフの $3$ つ組」であるとすると $(x,z,3xz-y)$ つまり \[\begin{aligned} (1,F_{2n+1},3\cdot 1\cdot F_{2n+1}-F_{2n-1}) &= (1,F_{2n+1},F_{2n+3}), \\ (1,P_{2n+1},3\cdot 2\cdot P_{2n+1}-P_{2n-1}) &= (2,P_{2n+1},P_{2n+3}) \end{aligned}\] も「マルコフの $3$ つ組」になるから, 数学的帰納法によりこの主張が成り立つ. ここで, 恒等式 \[ F_{2n+3} = 3F_{2n+1}-F_{2n-1}, \quad P_{2n+3} = 6P_{2n+1}-P_{2n-1}\] を使った (こちらを参照).
- 「マルコフの $3$ つ組」に現れる整数を「マルコフ数」と呼ぶ. 「マルコフ数」は有理数による実数の近似の問題に現れる: 任意の実数 $a$ に対して, \[\left| a-\frac{p}{q}\right| \leqq \frac{1}{\sqrt 5q^2}\] を満たす有理数 $\dfrac{p}{q}$ ($p,$ $q$: 整数, $q > 0$) が無限に存在する. この近似の精度が最も悪くなるのは,「黄金数」$\dfrac{1+\sqrt 5}{2}$ のように「連分数展開」の「部分商」がすべて $1$ の場合である. そのような実数を除くと, 上記の不等式は \[\left| a-\frac{p}{q}\right| \leqq \frac{1}{\sqrt 8q^2}\] に改めることができる. この近似の精度が最も悪くなるのは, $\sqrt 2$ のように「連分数展開」の「部分商」がすべて $2$ の場合である. そのような実数を除くと, 上記の不等式は \[\left| a-\frac{p}{q}\right| \leqq \frac{1}{\sqrt{\dfrac{221}{25}}q^2}\] に改めることができる. 同様の改善を続けていくときに現れる定数 $\sqrt 5,$ $\sqrt 8,$ $\sqrt{\dfrac{221}{25}},$ $\cdots$ は「ラグランジュ数」と呼ばれ, 一般に「マルコフ数」$m$ を用いて \[\sqrt{9-\frac{4}{m^2}}\] と表されることが知られている (参考: J・H・コンウェイ, R・K・ガイ著, 根上生也訳,『数の本』, 丸善出版, 2012).
- 「マルコフの方程式」は「フルヴィッツの方程式」$x_1{}^2+\cdots +x_n{}^2 = cx_1\cdots x_n$ の特別な場合である. $c > n$ のとき整数解は存在せず, $1 \leqq c \leqq n$ のときすべての整数解は有限個の整数解から生成されること, 特に $c = n$ のときすべての整数解は $(x_1,\cdots,x_n) = (1,\cdots,1)$ から生成されることが知られている.
- (B) の方程式 $(x+y)^2+(y+z)^2+(z+x)^2 = 12xyz$ の正の整数解について, 最近「マルコフ方程式」と類似の定理が発見された (行田康晃, $2021$ 年).
この方程式のすべての正の整数解は, $(1,1,1)$ から, $x,y,z$ の置換と $(x,y,z)$ を $(y,z,6yz-x-y-z)$ に対応させる変換の組合せにより構成できることが知られており, $x \leqq y \leqq z$ とすると次のような図にまとめられる.

問題《二重根号が外せる条件》
$s,$ $p$ を正の有理数 ($p$: 有理数の平方でない) とし, $\sqrt{s+2\sqrt p}$ が $\sqrt a+\sqrt b$ ($a,$ $b$: 正の有理数) の形に表されるとする.
このとき, $s^2-4p$ は有理数の平方であることを示せ.
解答例
\[\sqrt{a}+\sqrt b = \sqrt{(\sqrt a+\sqrt b)^2} = \sqrt{a+b+2\sqrt{ab}}\]
であるから, $\sqrt{s+2\sqrt p}$ が $\sqrt a+\sqrt b$ の形に表されるとき, ある有理数 $a,$ $b$ の和が $s,$ 積が $p$ になる.
このとき, $a,$ $b$ は $2$ 次方程式
\[ x^2-sx+p = 0\]
の有理数解になるから, その判別式 $s^2-4p$ は有理数の平方になる.
参考
- 正の有理数 $s,$ $p$ ($p$: 有理数の平方でない) に対して, $\sqrt{s\pm2\sqrt p}$ が $\sqrt a\pm\sqrt b$ ($a,$ $b$: 有理数, $a > b > 0$) の形に表されるためには, $s^2-4p$ が有理数の平方であることが必要十分である (こちらも参照).
- $ab = c^2$ ($c$: 正の有理数) であるとき, \[\sqrt a\pm\sqrt b = \sqrt a\pm\frac{c}{a}\sqrt{a} = \frac{a\pm c}{a}\sqrt a = \sqrt{\frac{(a\pm c)^2}{a}}\] は $1$ つの有理数の平方根として表される.
- $ab$ が有理数の平方でないとき, $\sqrt a,$ $\sqrt b$ の少なくとも一方は無理数であり, $\sqrt a\pm\sqrt b$ は $1$ つの有理数の平方根にはまとめられない.
問題《$3$ 次方程式の判別式》
$3$ 次方程式 $x^3+3px+2q = 0$ ($p,$ $q$: 実数) が解 $x = \alpha,$ $\beta,$ $\gamma$ をもつとする.
- (1)
- $p,$ $q$ を用いて $\alpha ^2+\beta ^2+\gamma ^2,$ $\alpha ^2\beta ^2+\beta ^2\gamma ^2+\gamma ^2\alpha ^2$ を表せ.
- (2)
- $p,$ $\alpha$ を用いて $(\gamma -\alpha )(\alpha -\beta )$ を表せ.
- (3)
- $p,$ $q$ を用いて $(\alpha -\beta )^2(\beta -\gamma )^2(\gamma -\alpha )^2$ を表せ.
解答例
- (1)
- 解と係数の関係により \[\begin{aligned} \alpha +\beta +\gamma &= 0 \quad \cdots [1], \\ \alpha\beta +\beta\gamma +\gamma\alpha &= 3p \quad \cdots [2], \\ \alpha\beta\gamma &= -2q \quad \cdots [3] \end{aligned}\] が成り立つから, \[\begin{aligned} &\alpha ^2+\beta ^2+\gamma ^2 \\ &= (\alpha +\beta +\gamma )^2-2(\alpha\beta +\beta\gamma +\gamma\alpha ) \\ &= 0^2-2\cdot 3p \\ &= -6p, \\ &\alpha ^2\beta ^2+\beta ^2\gamma ^2+\gamma ^2\alpha ^2 \\ &= (\alpha\beta +\beta\gamma +\gamma\alpha )^2-2\alpha\beta\gamma (\alpha +\beta +\gamma ) \\ &= (3p)^2-2\cdot (-2q)\cdot 0 \\ &= 9p^2 \end{aligned}\] である.
- (2)
- $[1],$ $[2]$ から, \[\begin{aligned} &(\gamma -\alpha )(\alpha -\beta ) = -(\alpha -\beta )(\alpha -\gamma ) \\ &= -\alpha ^2+(\beta +\gamma )\alpha -\beta\gamma \\ &= -\alpha ^2+(-\alpha )\alpha -\{ 3p-\alpha (\beta +\gamma )\} \\ &= -\alpha ^2-\alpha ^2-3p+\alpha (-\alpha ) \\ &= -3(\alpha ^2+p) \end{aligned}\] が成り立つ.
- (3)
- (2) と同様に \[\begin{aligned} (\alpha -\beta )(\beta -\gamma ) &= -3(\beta ^2+p), \\ (\beta -\gamma )(\gamma -\alpha ) &= -3(\gamma ^2+p) \end{aligned}\] も成り立つから, \[\begin{aligned} &(\alpha -\beta )^2(\beta -\gamma )^2(\gamma -\alpha )^2 \\ &= (\gamma -\alpha )(\alpha -\beta )\cdot (\alpha -\beta )(\beta -\gamma )\cdot (\beta -\gamma )(\gamma -\alpha ) \\ &= -27(\alpha ^2+p)(\beta ^2+p)(\gamma ^2+p) \\ &= -27\{ (\alpha\beta\gamma )^2+p(\alpha ^2\beta ^2+\beta ^2\gamma ^2+\gamma ^2\alpha ^2) \\ &\qquad +p^2(\alpha ^2+\beta ^2+\gamma ^2)+p^3\} \\ &= -27\{ (-2q)^2+p\cdot 9p^2+p^2\cdot (-6p)+p^3\} \\ &= -27(4p^3+4q^2) \\ &= -108(p^3+q^2) \end{aligned}\] である.
参考
- 重複度込みで $n$ 個の解 $\alpha _1,$ $\cdots,$ $\alpha _n$ をもつ $n$ 次方程式 $a_nx^n+\cdots +a_1x+a_0 = 0$ の「判別式」(discriminant) $D$ は
\[ D = a_n{}^{2n-2}\prod _{1 \leqq k < l \leqq n}(\alpha _k-\alpha _l)^2\]
で定義される.
ここで, $\displaystyle\prod _{1 \leqq k < l \leqq n}(\alpha _k-\alpha _l)^2$ は $1 \leqq k < l \leqq n$ なるすべての番号の組 $(k,l)$ にわたる $(\alpha _k-\alpha _l)^2$ の積を意味する.
$D = 0$ $\iff$ $[*]$ が重解をもつが成り立つ.
- $3$ 次方程式 $a_3x^3+a_2x^2+a_1x+a_0 = 0\ \cdots [*]$ ($a_k$: 複素数) の「判別式」$D$ は
\[ D = 18a_3a_2a_1a_0-4a_3a_1{}^3-27a_3{}^2a_0{}^2+a_2{}^2a_1{}^2-4a_2{}^3a_0\]
である.
実数係数のとき, 次のことが知られている (こちらを参照).
- $D > 0$ のとき, $[*]$ は $3$ 個の相異なる実数解をもつ.
- $D < 0$ のとき, $[*]$ は $1$ 個の実数解と $1$ 組の共役な虚数解をもつ.
- $3$ 次方程式 $x^3+a_2x^2+a_1x+a_0 = 0$ ($a_k$: 実数) は, $x = X-\dfrac{a_2}{3}$ とすると, $X^3+3pX+2q = 0$ ($p,$ $q$: 実数) の形に変形できる. この変数の置き換えは「カルダーノ変換」(Cardano's transformation) と呼ばれる.
